2021阿里巴巴校招笔试真题_Java工程师、C++工程师_牛客网
6.在一个地区有 n个城市以及 n?1条无向边,每条边的时间边权都是 1,并且这些城市是联通的,即这个地区形成了一个树状结构。每个城市有一个等级。
现在小强想从一个城市走到另一个不同的城市,并且每条边经过至多一次,同时他还有一个要求,起点和终点城市可以任意选择,但是等级必须是相同的。但是小强不喜欢走特别远的道路,所以他想知道时间花费最小是多少。
解:?用双重循环,得到节点对再深搜,最后一个样例会超时。故改为以每个节点为起点做dfs,以等级相同为结束条件。
#include<stdio.h>
#include<math.h>
#include<vector>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
int n,a[5005],root;
vector<int> g[5005];
int minstep;
void dfs(int cur,int before,int step)
{
if(cur!=root&&a[cur]==a[root])
minstep=min(minstep,step);
for(int i=0;i<g[cur].size();i++)
{
if(g[cur][i]!=before)
dfs(g[cur][i],cur,step+1);//避免与上一个节点重复
}
}
int main()
{
int i,j,k,u,w;
minstep=1e9;
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d",&a[i]);
for(i=0;i<n-1;i++)
{
scanf("%d%d",&u,&w); //无向边
g[u-1].push_back(w-1);
g[w-1].push_back(u-1);
}
for(i=0;i<n;i++)
{
root=i;
dfs(i,0,0);
}
if(minstep!=1e9)
printf("%d\n",minstep);
else
printf("-1\n");
}
7.有n个牛牛一起去朋友家吃糖果,第i个牛牛一定要吃ai块糖果。而朋友家一共只有m块糖果,可能不会满足所有的牛牛都吃上糖果。同时牛牛们有k个约定,每一个约定为一个牛牛的编号对(i,j),表示第i个和第j个牛牛是好朋友,他俩要么一起都吃到糖果,要么一起都不吃。
保证每个牛牛最多只出现在一个编号对中。您可以安排让一些牛牛吃糖果,一些牛牛不吃。
要求使能吃上糖果的牛牛数量最多(吃掉的糖果总量要小于等于m),并要满足不违反牛牛们的k个约定。
解:将约定的两只牛牛绑定,糖数相加并记作人数2,转为01背包问题。
#include<stdio.h>
#include<math.h>
#include<vector>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
int dp[10005];
struct q{
int a,v;
}p[1005];
int cmp(q x,q y)
{
if(x.a!=y.a)
return x.a<y.a;
return x.v>y.v;
}
int main()
{
int n,m,i,j,k,u,w;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
{
scanf("%d",&p[i].a);
p[i].v=1;
}
scanf("%d",&k);
for(i=0;i<k;i++)
{
scanf("%d%d",&u,&w);
p[u].a+=p[w].a;
p[u].v=2;
p[w].a=1e7;
p[w].v=0;
}
sort(p+1,p+1+n,cmp);
for(i=1;i<=n;i++)
{
if(p[i].v==0)
continue;
for(j=m;j>=p[i].a;j--)
dp[j]=max(dp[j],dp[j-p[i].a]+p[i].v);
}
printf("%d\n",dp[m]);
}8.有这样的一个方格游戏:这个游戏是这样的:
1.有n*m个方格,方格内每一个位置都有一个数,代表到达这个点后拥有的能量。
2.初始的时候在左上角,并将左上角的值作为初始能量,终点为右下角的点。
3.每一步只能往下或者往右走,且走一步需要消耗1点能量。不能在原地停留,即不会获得中间节点的能量并且能量不累计。
4.当你选择了一条可行的路径(这条路径消耗的能量不超过现有能量),你可以走到终点。
例如:
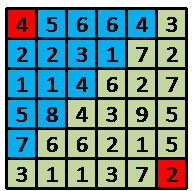
最开始在(1,1)点,拥有的是4点能量,蓝色的方格代表从起点出发4步以内所能走到的点,假设我们第一次走到(3,2),则到达后能量变为1点,那么接下来可以达到的点为(3,3)和(4,2)。
现在想问你有多少条不同的路径(两条路径如果按顺序依次到达的点有一个不同,则认为是不同的路径方式)可以从左上角的点走到右下角的点,由于答案很大,请答案对10000取余。
?解:地图不大,直接dp暴力从a[i][j]走到a[k][l]的所有可能。
#include<stdio.h>
#include<math.h>
#include<vector>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
int a[105][105];
int main()
{
int t,n,m,i,j,k,l,u,w;
scanf("%d",&t);
while(t--)
{
int dp[105][105]={0};
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
scanf("%d",&a[i][j]);
}
dp[0][0]=1;
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
//从a[i][j]走到a[k][l]
for(k=i;k<=i+a[i][j]&&k<n;k++)
{
for(l=j;l<=j+a[i][j]&&l<m;l++)
{
if(k==i&&l==j)continue;
if(k+l-i-j<=a[i][j])
dp[k][l]+=dp[i][j]%10000;
}
}
}
}
printf("%d\n",dp[n-1][m-1]%10000);
}
}
9.小强有一个长度为n的数组a和正整数m。他想请你帮他计算数组a中有多少个连续的子区间[l,r],其区间内存在某个元素出现的次数不小于m次?
例如数组a=[1,2,1,2,3]且m=2,那么区间[1,3],[1,4],[1,5],[2,4],[2,5]都是满足条件的区间,但区间[3,4]等都是不满组条件的。
解:这是一道经典滑动窗口题。边读入边统计a出现的位置i存入vector,当次数==m时,子区间满足条件。固定子区间的右端点,移动左端点,可得覆盖该子区间的其他解。需要注意左端点须与之前出现过的左端点取max,不然会出现多次覆盖。
#include<stdio.h>
#include<math.h>
#include<vector>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
//本题sum会超过int范围,需要用long long
vector<int> v[400050];
int main()
{
int a,n,m,i,l=0;
long long sum=0;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
{
scanf("%d",&a);
v[a].push_back(i);
if(v[a].size()==m)
{
l=max(l,v[a][0]);//左边界:取靠右的下标,避免重复计算
v[a].erase(v[a].begin());//去掉第一个值
}
sum+=l;
}
printf("%lld\n",sum);
}
10. 小强有两个序列a和b,这两个序列都是由相同的无重复数字集合组成的,现在小强想把a序列变成b序列,他只能进行以下的操作:
从序列a中选择第一个或者最后一个数字并把它插入a中的任意位置。
问小强至少需要几次操作可以将序列a变为序列b。
解:将问题转为最长字串(连续的最长子序列) 问题,把序列a的值转为序列b中的对应位置,具体可以看代码注释中的例子。
#include<stdio.h>
#include<math.h>
#include<map>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
int n,a[100005],b;
map<int,int>mp;
// 求a对应b的位置的最长子串(连续的最长子序列)
int main()
{
int i,j,ans=0,cnt=0;
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&a[i]); // 453216
for(i=1;i<=n;i++)
{
scanf("%d",&b); // 643215
mp[b]=i;
}
for(i=1;i<=n;i++)
{
a[i]=mp[a[i]]; // 将a由值变成b的位置,即 163451
//printf("%d ",a[i]);
}
for(i=2;i<=n;i++)
{
if(a[i]>a[i-1])
ans=max(ans,++cnt);
else
cnt=1;
}
printf("%d\n",n-ans); // 最长字串是345
return 0;
}