蓝桥杯练习014
FBI树
问题描述
我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2^n的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
1)T的根结点为R,其类型与串S的类型相同;
2)若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2^n的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
输入格式
第一行是一个整数N(0 <= N <= 10),第二行是一个长度为2N的“01”串。
输出格式
包括一行,这一行只包含一个字符串,即FBI树的后序遍历序列。
样例输入
3
10001011
样例输出
IBFBBBFIBFIIIFF
数据规模和约定
对于40%的数据,N <= 2;
对于全部的数据,N <= 10.
解题思路
二分法解决问题
运用递归
先处理左边,然后右边
分别计数
对结果进行处理输出结果
代码示例
#include <iostream>
#include<string>
using namespace std;
string str;
void fun(int left,int right){
if(left>right)return;
int CntB=0,CntI=0;//记录B和I的数量
int mid=(left+right)/2;//求中间的位置
if(left!=right){
fun(left,mid);//递归处理左边的部分
fun(mid+1,right);//处理右边的部分
}
while(left<=right){
if(str[left++]=='0')//为0时B的数量加一
CntB++;
else
CntI++;//I的数量增加1
}
if(CntB!=0&&CntI!=0)cout<<"F";//0 1 都有,输出F
else if(CntB!=0&&CntI==0)cout<<"B";//只有0
else cout<<"I";//只有1
}
int main()
{
int n;
cin>>n;
cin>>str;
fun(0,str.length()-1);
cout<<endl;
return 0;
}
完全二叉树的权值(2019 年省赛)
题目描述
给定一棵包含 N个节点的完全二叉树,树上每个节点都有一个权值,按从 上到下、从左到右的顺序依次是 A1,A2,???A**N*,如下图所示:
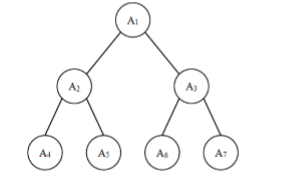
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点 权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1。
输入描述
第一行包含一个整数N*(1≤*N≤10^5)。
第二行包含 N 个整数 A1,A2,???AN (?10^5 ≤Ai≤10^5)。
输出描述
输出一个整数代表答案。
输入输出样例
示例
输入
7
1 6 5 4 3 2 1
输出
2
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
代码示例
#include <iostream>
#include<cmath>
using namespace std;
typedef long long ll;
ll n,i,j;
ll maxx=-100000;
ll a[100010];
void fun(ll n)
{
ll m=n;
ll k=0;//层数
ll flag;//标记
while(m){
m/=2;
k++;
}//循环结束后k为二叉树的层数
ll sum;//总和
for(i=1;i<k;i++){//遍历每一层
sum=0;
ll t1=pow(2,i-1);//前i-1层的数目
ll t2=pow(2,i);//前i层的数目
for(j=t1;j<=t2-1;j++){
sum+=a[j];//将第i层的数据加起来
}
if(sum>maxx){
maxx=sum;//如果超过最大值,更新并标记位置
flag=i;
}
}
sum=0;
for(i=pow(2,k-1);i<=n;i++){//k-1层到n层
sum+=a[i];
}
if(sum>maxx){
maxx=sum;
flag=k;
}
cout<<flag<<endl;
}
int main()
{
// 请在此输入您的代码
cin>>n;
for(i=1;i<=n;i++)
cin>>a[i];//读入数据
fun(n);//处理
return 0;
}