轮盘赌法及其 java 实现
一、轮盘赌法介绍
轮盘赌法是一种常用的随机算法,在计算机模拟随机应用中广泛使用
其目的,是为了让个体被选择的次数,遵循个体在总体中的适应度及选择概率
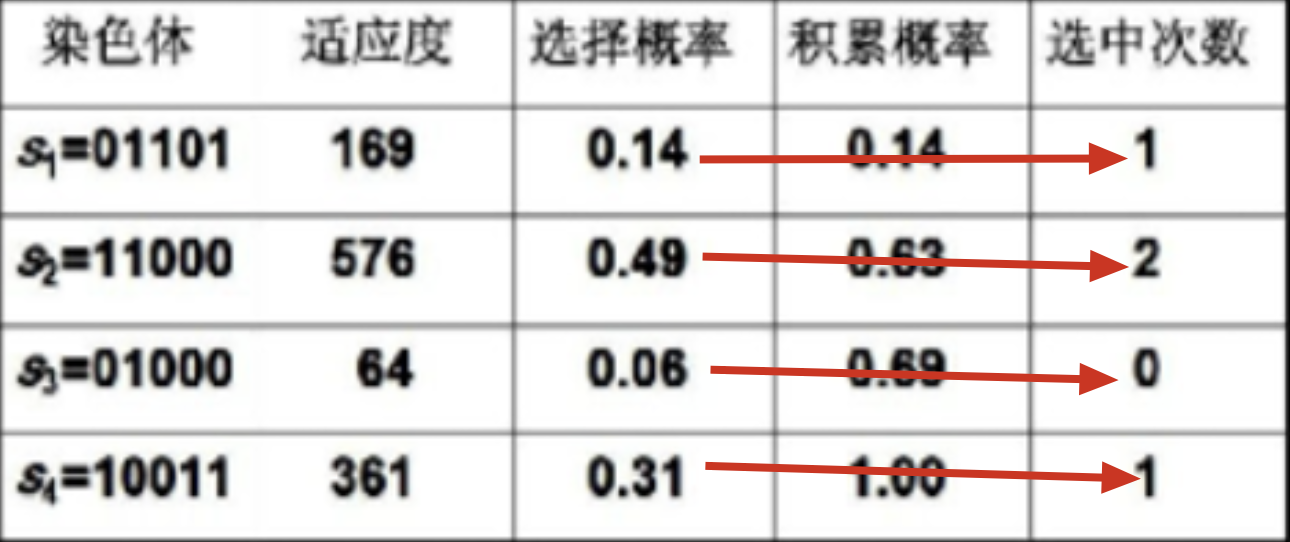
在遗传算法的父代筛选过程中,轮盘赌法被广泛使用
二、轮盘赌法的实现
这里我们要先计算个体适应度占到总适应度的比值,即获取其选择概率(选择概率之和要保证为1)
然后,通过随机选取总概率片段,遍历累加种群的个体选择概率,直到累加和大于或者等于之前获取的随机概率片段,我们就选择它
我借助下面的图来说明一下,0.14 的概率想要被选中,只有在随机片段长度为 0 - 0.14 才有可能,0.49 的概率片段想要被选中,只有在随机概率片段长度为 0.14 - 0.63 才会被选中。可以发现,每个概率片段被选中的可能性与其被选概率是一致的
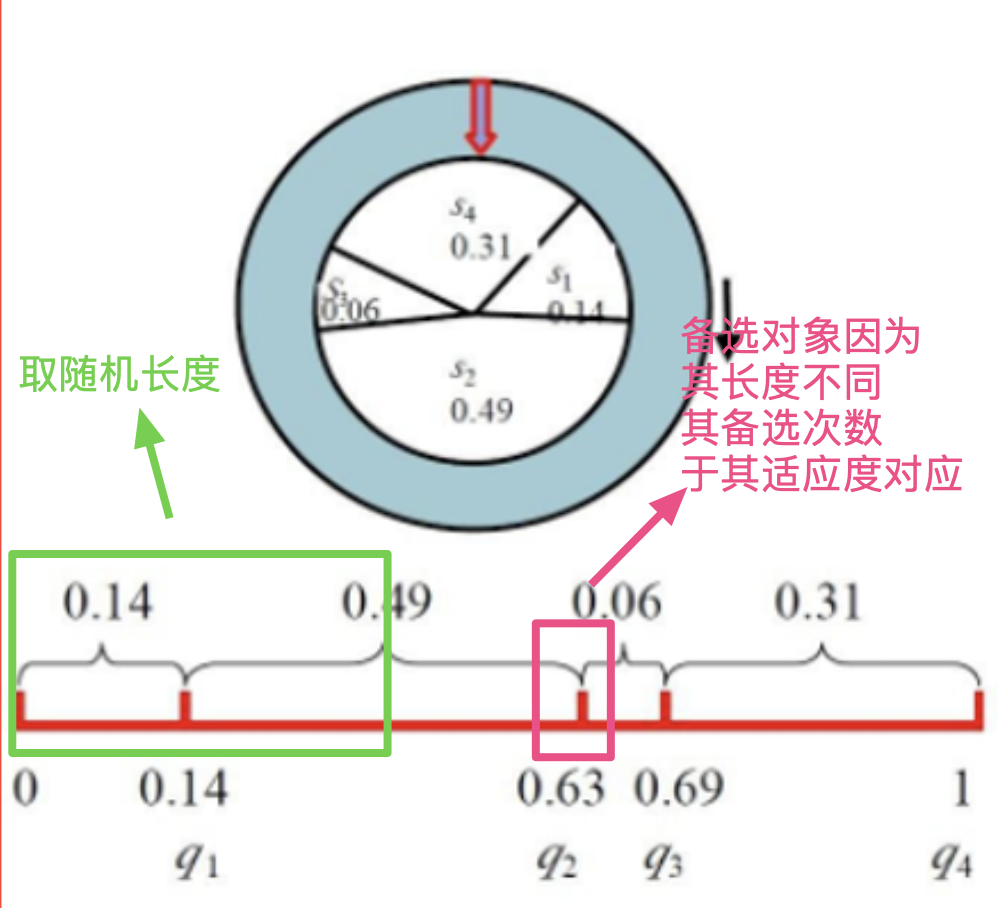
当然,处于计算机精度的考量,使用小数计算可能会导致种群概率总和小于或大于1,在面对海量数据的情况下,这种微小的差距可能带来难以想象的后果,所以我们也可以使用适应度和总适应度代替个体被选概率和总概率
三、轮盘赌法的实现代码
public class Roulette {
private static int iterTime = 100;
public static void main(String[] args) {
int[] seq = new int[]{13,7,25,41,14};
System.out.println("迭代次数为100的情况下,各数被选择的次数分别为:");
HashMap<Integer, Integer> selectTime = getSelectTime(iterTime, seq);
for (Integer key : selectTime.keySet()) {
System.out.println(key+" : "+selectTime.get(key));
}
}
/**
* 使用轮盘赌法,
* 获取不同适应度在规定迭代次数内被选择的次数
* @param iterNum 迭代次数
* @param seq 种群
* @return
*/
public static HashMap<Integer, Integer> getSelectTime(int iterNum, int[] seq) {
HashMap<Integer, Integer> map = new HashMap<>();
int total = 0;
for (int elem : seq) {
total+=elem;
}
for (int i = 0; i < iterNum; i++) {
double slice = total * Math.random();
int sum = 0;
for (int j = 0; j < seq.length; j++) {
sum+=seq[j];
if (sum>slice) {
map.put(seq[j],map.getOrDefault(seq[j],0)+1);
break;
}
}
}
return map;
}
}
运行结果如下:





可以看到,个体被选择的次数,与其适应度是大致对应的
四、为什么遗传算法中要使用轮盘赌法选择父代
我们知道,遗传算法有一步,是选择两个优秀父代,进行位交换,从而生成两个相对优秀的子代的
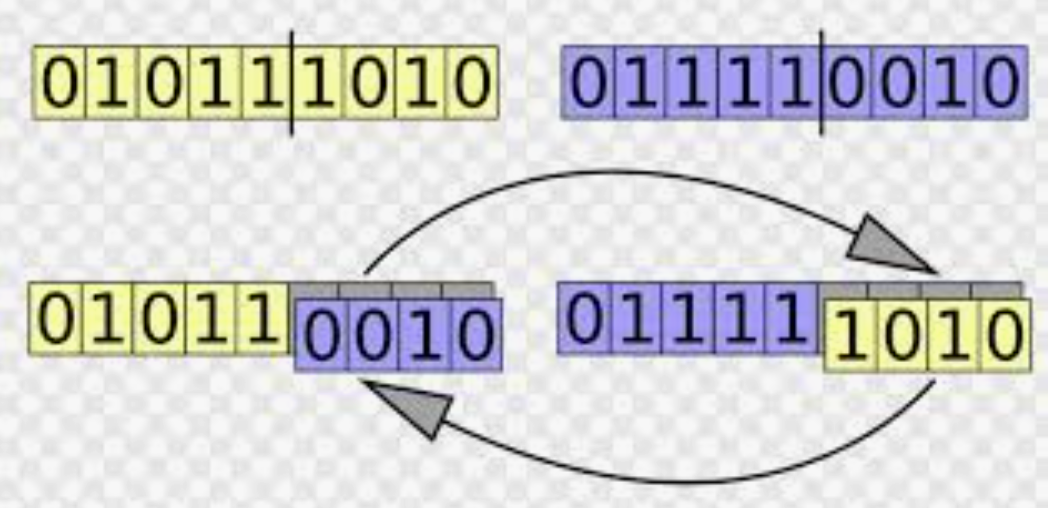
如果说,我们不使用轮盘赌法,那么父代的选择就只剩下两种策略:只选最优和随机策略
我来分别探讨一下两种策略的缺点
- 只选最优
如果我们每次只选最优秀的第 1、2个父代(甚至两个都是最优的那个父代),那么,在第二次迭代后,所有子代的相似度就会非常大(这里之所以不说一样,是因为交换位的生成是随机的)
因为不能保证初始种群的最佳父代就包含了最佳结果,那么,因为子代的变化差异不明显,所以迭代次数会成倍增加。极大地消耗我们的算力和时间,不可取
- 随机策略
使用随机策略,虽然我们的子代差异性大大增加了,但是如果哪次选择,适应度最差的父代撞了大运,每次都被选中,那么相应的,产生的子代种群适应度总和可能不升反降
我们的算法就会变得十分不稳定,最坏的情况,就是迭代结束之后,种群适应度总和甚至会比初始种群还低
综上所述,轮盘赌法即保证了随机策略的差异性,又保证了父代尽量优秀的特点,所以其是遗传算法交叉步骤中必选的方法