基本概念
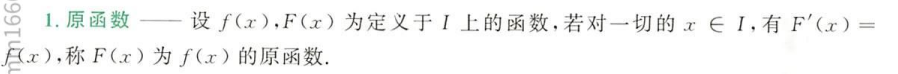


不定积分基本公式与积分法
基本公式

推导待定
积分法
换元积分法
第一类换元积分法(凑微分法)

观察上面三个例子可得
- 把dx换成d其他东西,是为了能够在d之后出来一个前面式子的东西
- 然后把前面式子给简化掉,变成可以用基本公式的样子

这题怎么说呢,以为是会了,但是做的时候还是有差距,就是你还是得一步一步来,尽量把你的式子的尽量多的东西换成你要代换的东西

- 你大可以把式子拆成两个,然后两边根据情况用d后面放不同的东西
第二类换元积分法
**原理:**是让x变成一个t的表达式,和第一类刚好相反(把x的一个表达式换成t)
使用情形:
1.将被积函数从无理函数转化为有理函数
但是遇到无理函数不一定就一定要用第二类换元积分法
例如

这两个变换稍微挖空一下吧

在最后那一个结论的第二个项挖个空吧

- 这是第二类积分法的应用,把必须解决的无理的东西换成有理的。就是把x换成一个t的表达式让它有理
- 然后注意一下那个t/1+t积分的拆分方法
2.当被积函数含平方和或者平方差的时候用三角代换

sin是对边和斜边的比值
tan是对边和邻边的比值
sec是斜边和邻边的比值
csc是斜边和对边的比值(刚好是1/sin)
sec是斜边和邻边的比值(刚好是1/cos)
然后你看表达式的样子
- 如果是平方差,x2 是被减数,那么代表a是斜边了,用t表示x是asint
- 如果是平方差,但是x2是减数,那么代表x是斜边了,用t表示x是asect
- 如果是平方和,那么就代表这两条边是除了斜边的两条边,用t表示x是atant

最后可以画一个三角形来把t变回x
