哈夫曼树及其应用

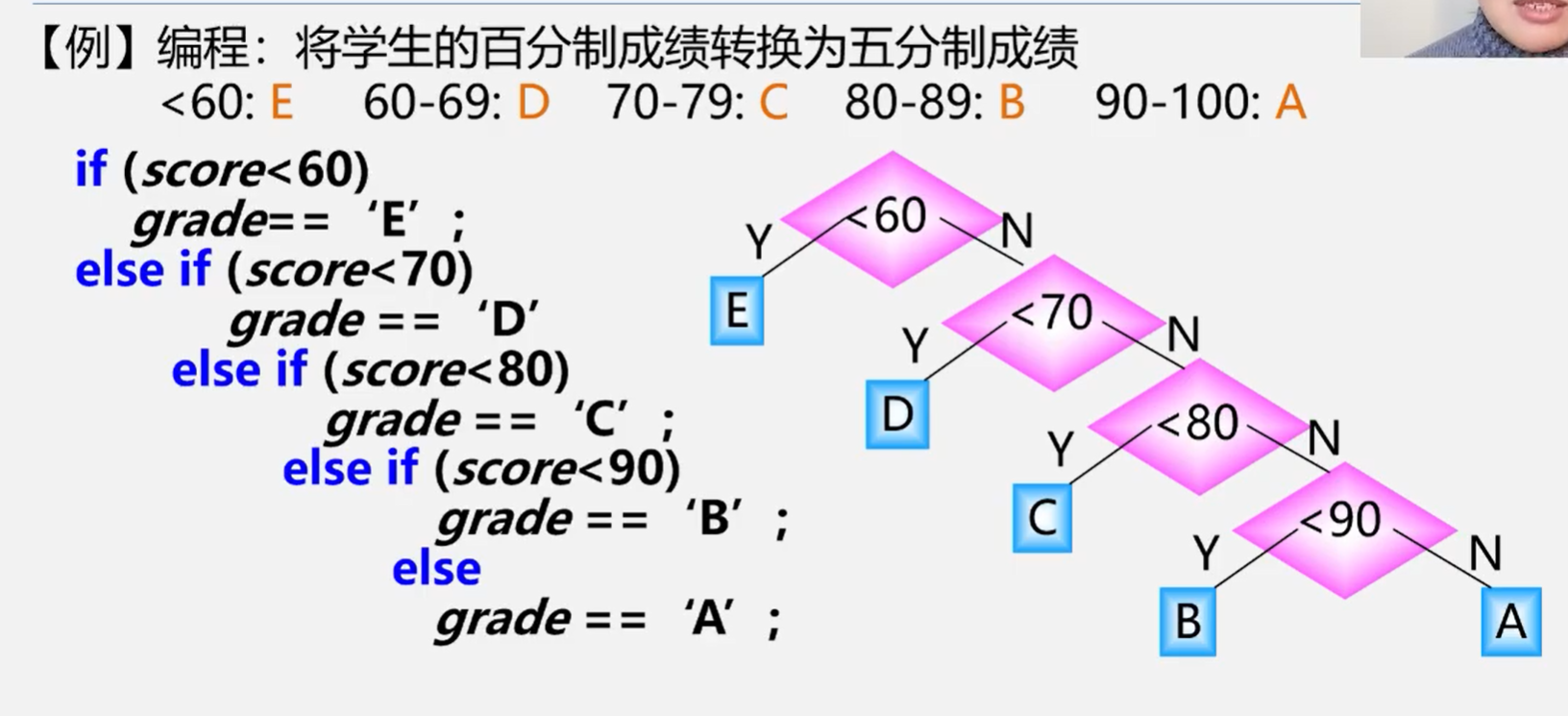
判断树:用于描述分类过程的二叉树
假设 小于60分的同学有5% 60-70 15% 70-80 40% 80-90 30% >90 10%

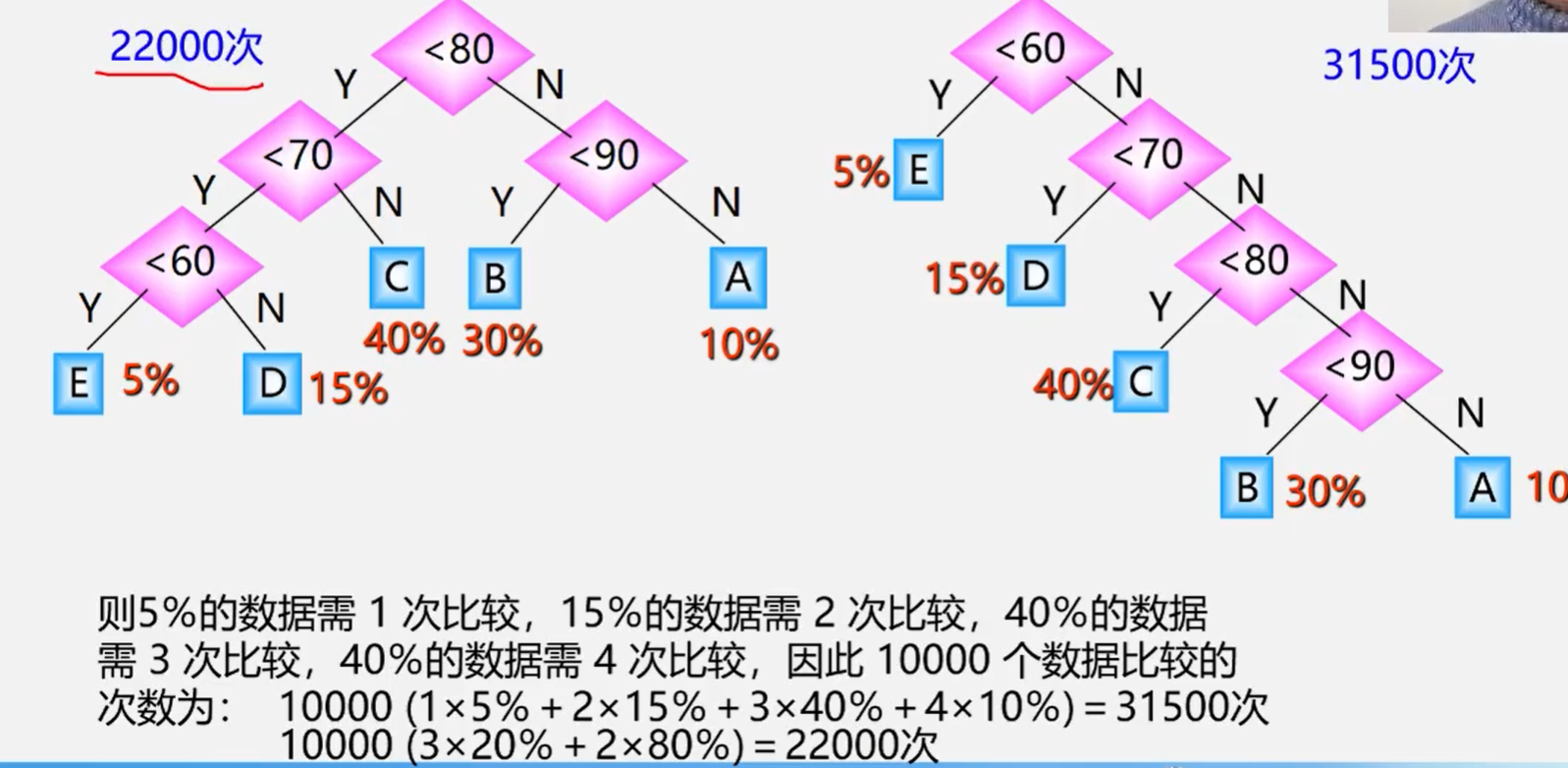
显然:两种判别树的效率是不一样的
问题:能不能找到一种效率最高的判别树呢? 这就是哈夫曼树(最优二叉树)研究的问题
哈夫曼树基本概念
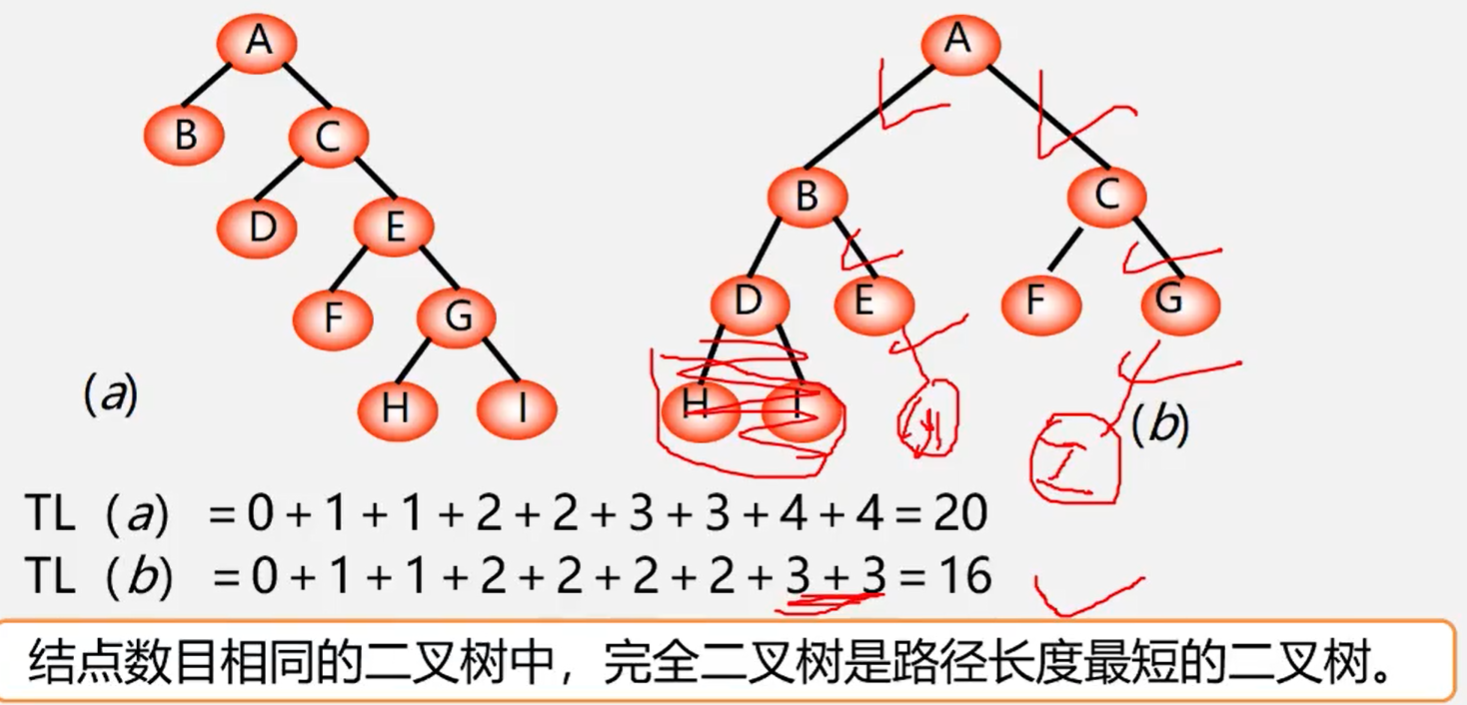
树的路径长度:
从树根到每一个节点的路径长度之和,记作TL
权
将树种结点赋给一个有着某种含义的数值,则这个数值称为该结点的权
节点的带权路径长度
从根节点到该结点之间的路径长度与该节点的权的乘积
树的带权路径长度
树种所有的叶子节点的带权路径长度之和

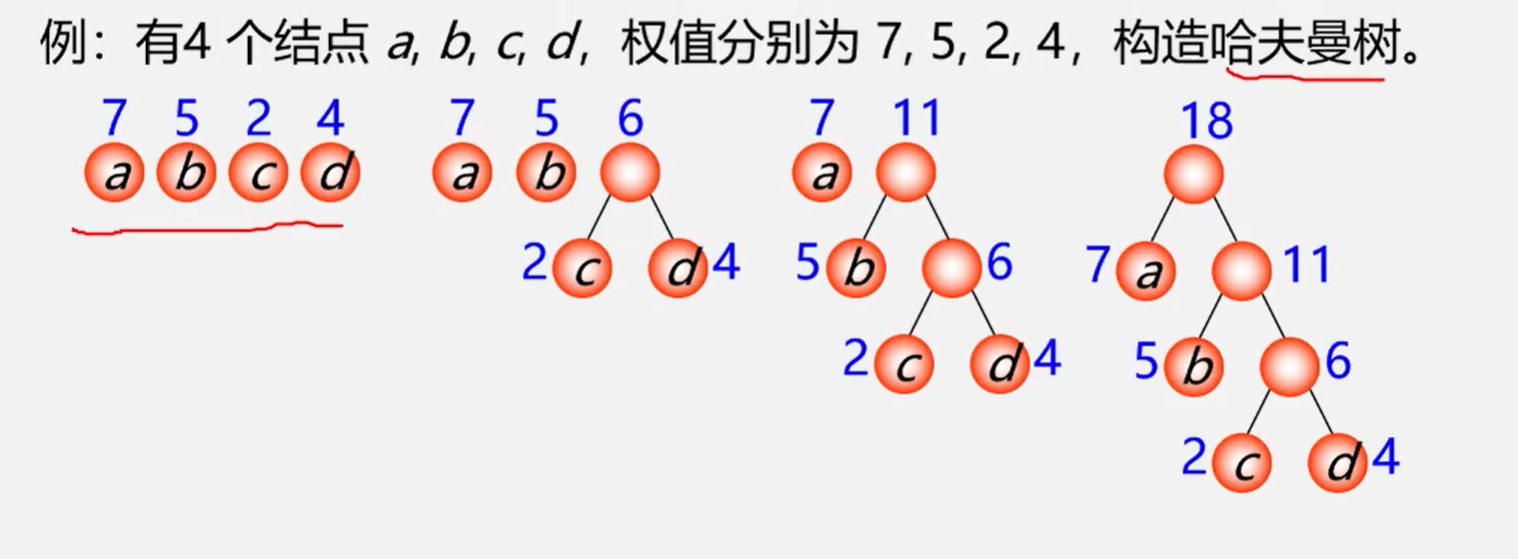
例子:有四个节点 a,b,c,d权值分别为7,5,2,4构造以此4个结点为叶子节点的二叉树
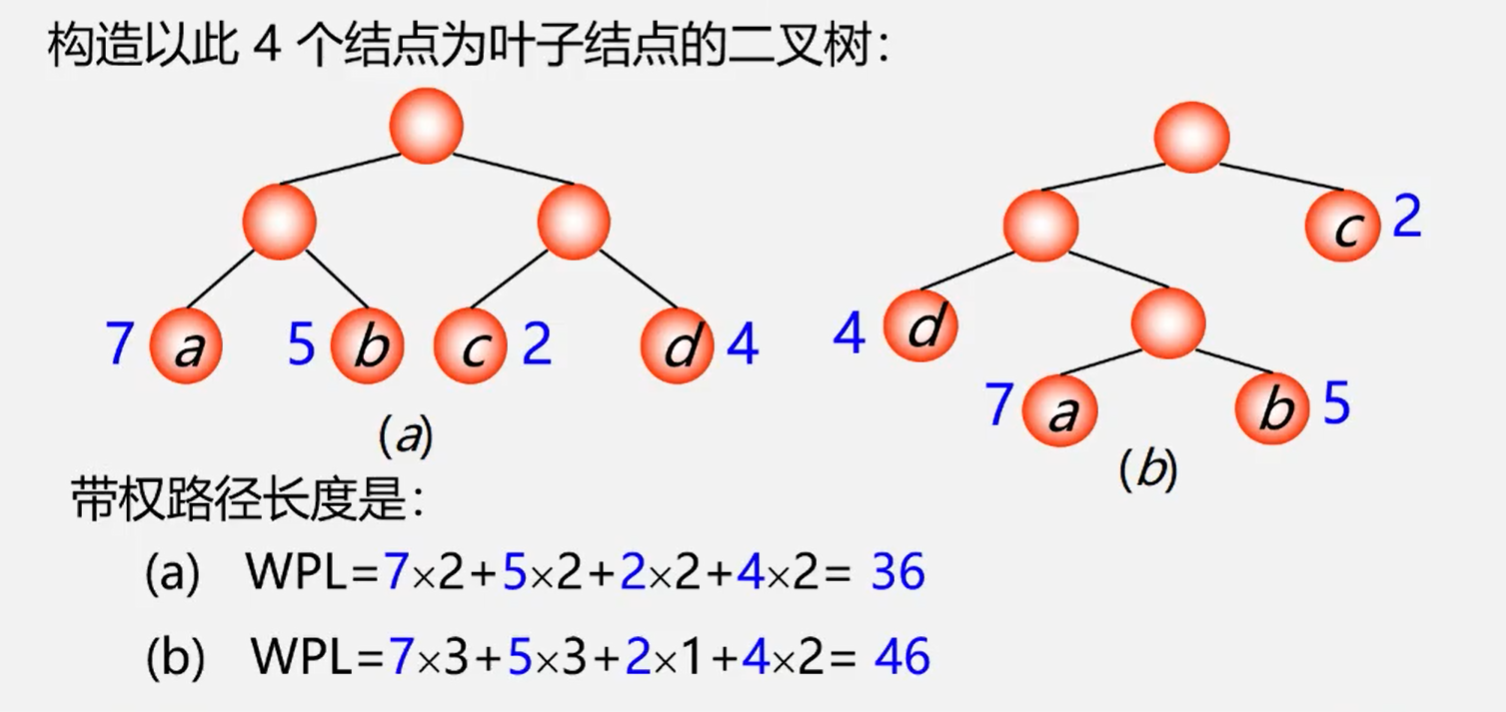
哈夫曼树:最优树 带权路径(WPL)最短的书
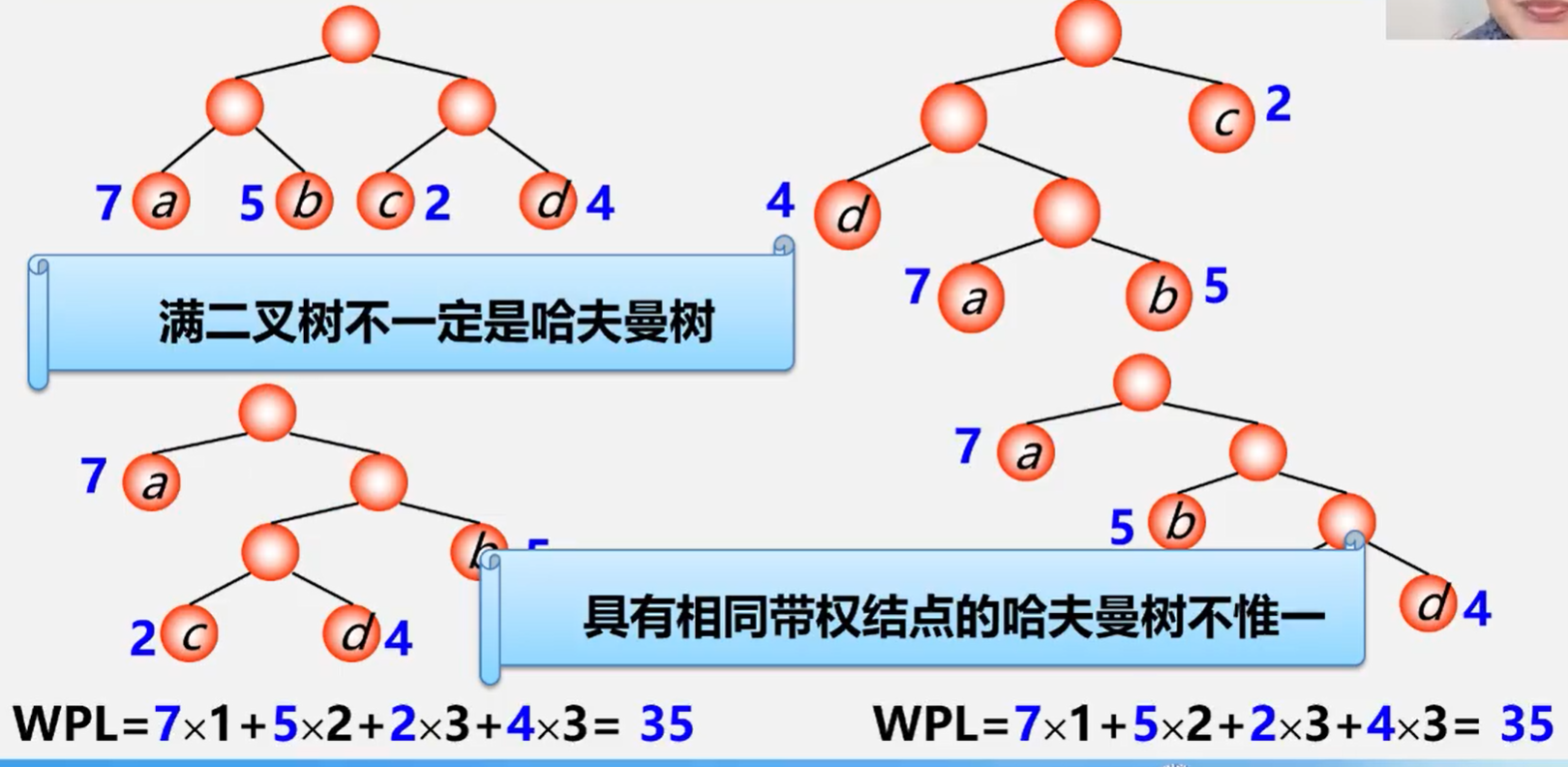
带权路径最短 是在 度相同 的树中比较而得的结果,英雌有最优二叉树、最优三叉树之称等
哈夫曼树:最优二叉树 带权路径最短(WPL)的二叉树
应为构造这种树的算法是由哈夫曼教授与1952年提出的没所以被称为哈夫曼树,相应的算法称为哈夫曼算法
哈夫曼树构造算法
哈夫曼树中权越大的叶子离根越近 贪心算法:构造哈夫曼树时首先选择权值小的叶子节点

哈夫曼算法口诀
- 构造森林全是根
- 选用两小造新树
- 删除两小添新人
- 重复2,3剩单根
总结
- 在哈夫曼算法中,初始时有n棵二叉树,要经过n-1次合并最终形成哈夫曼树
- 经过n-1次合并产生n-1个新节点,且这n-1个新节点都是具有两个孩子的分支节点
- 可见:哈夫曼树中共有 n+n-1=2n-1个结点,且其所有的分支节点的度均布唯一
哈夫曼树构造算法的实现
采用顺序存储结构------ 一维结构数组
结点类型定义
哈夫曼编码
- 在远程通讯中,要将待传字符串转换成由二进制的字符串
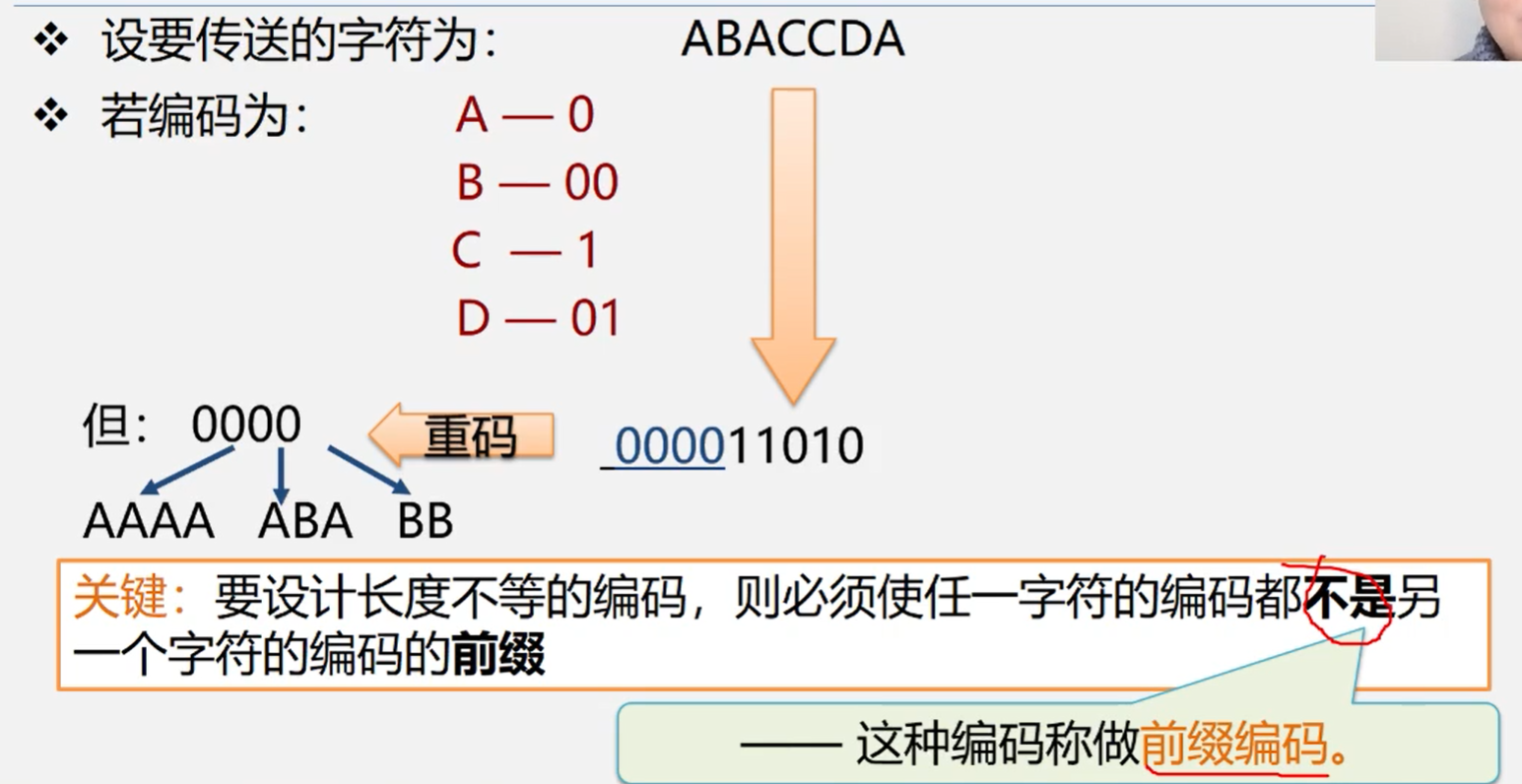
直接传输占据的内存空间太大,采用下面这种格式容易造成多义

注意:左小右大是一种习惯 不唯一
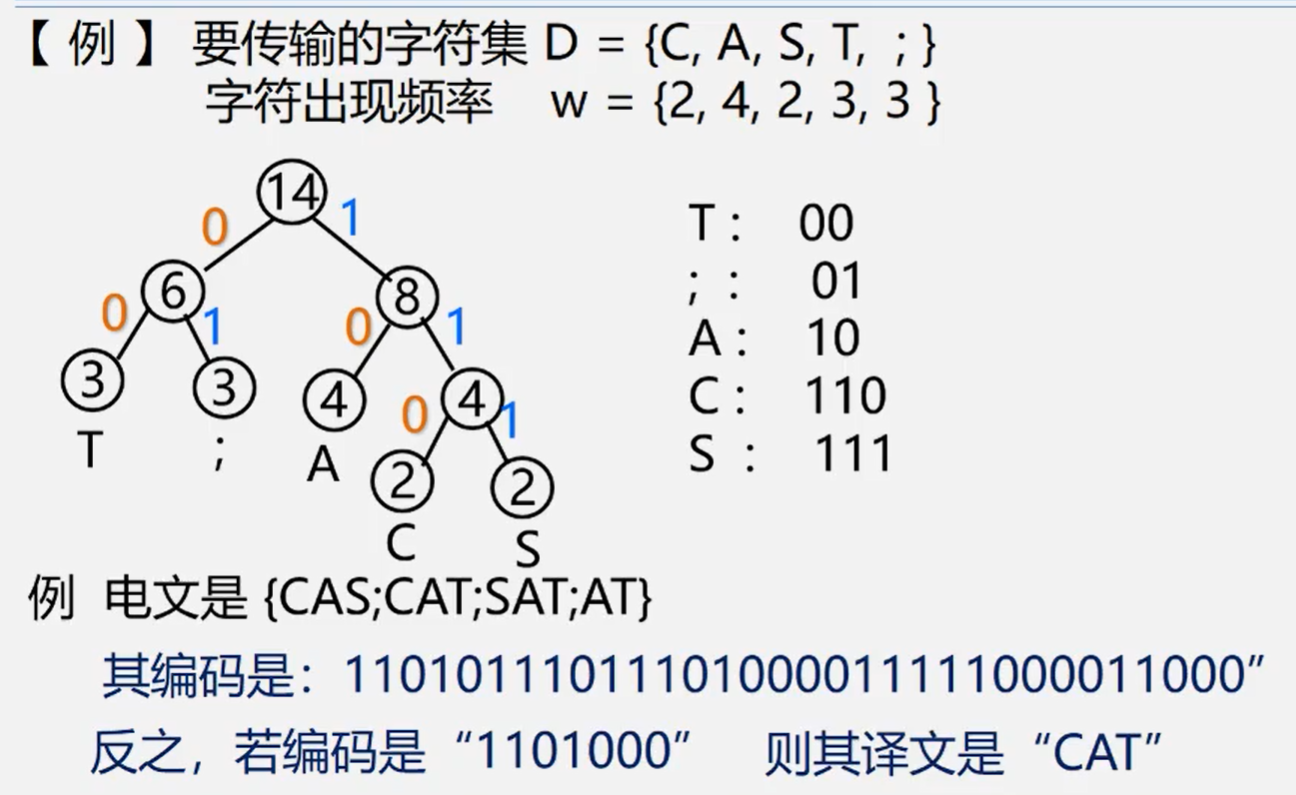
两个问题:
- 为什么哈夫曼编码能够保证是浅醉编码
- 因为 没有一片树叶是另一片树叶的祖先,所以每个叶节点的编码就不肯恶搞是其他叶结点编码的前缀
- 为什么哈夫曼树能够保证字符编码总长最短
- 因为 哈弗马上农户的带权路径长度最短,故字符编码的总长最短
哈夫曼编码是前缀码
哈夫曼编码是最有前缀码
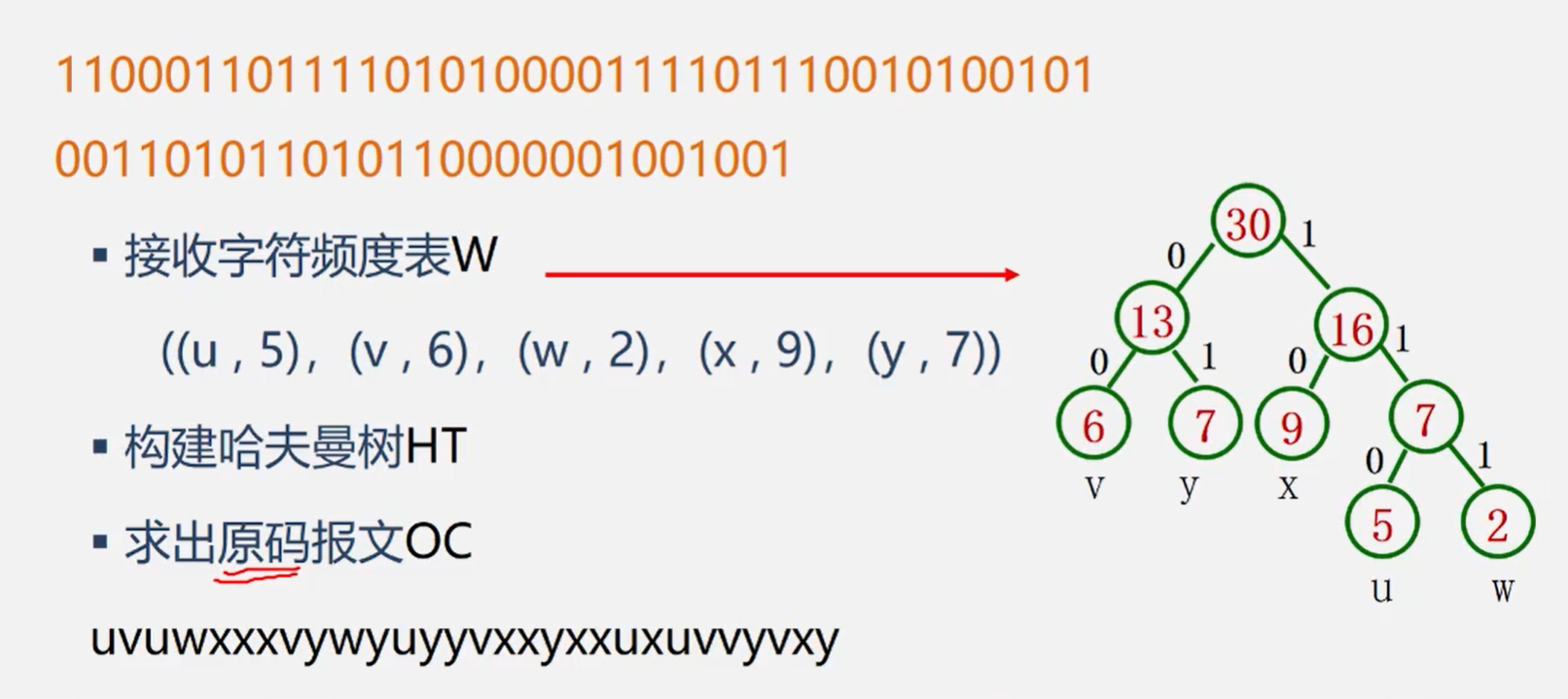
文件的编码和解码

原理是统计每个数字出现的次数,他的次数也就是他的权,根据他的权我们需要构造哈夫曼树,然后再按照左小右大构建每个单词的哈夫曼编码
编码:
- 输入各字符及其权值
- 构造哈弗马上农户–HT[I]
- 进行哈夫曼编码----HC[i]
- 差HC[I],得到各字符的哈夫曼编码
解码
- 构造哈夫曼树
- 一次读入二进制码
- 读入0,则走向左孩子;读入1,则走向该右孩子
- 一旦到达某叶子时,即可翻译出字符
- 然后再从根出发继续译码,直到结束
C[i]
4. 差HC[I],得到各字符的哈夫曼编码
解码
- 构造哈夫曼树
- 一次读入二进制码
- 读入0,则走向左孩子;读入1,则走向该右孩子
- 一旦到达某叶子时,即可翻译出字符
- 然后再从根出发继续译码,直到结束