回溯、贪心、动态规划的思路是通过大量做题培养的,不是说几天就能掌握,而且题目不会告诉你使用哪个算法。坚持做题。。。
回溯——46. 全排列(中等) 51.N皇后 (困难)
前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行。 「路径」和「选择」是每个节点的属性
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
这里稍微做了些变通,没有显式记录「选择列表」,而是通过 used 数组记录 track 中的元素,从而推导出当前的选择列表。

JS语法——复制数组
[…path]
Array.from(path)
path.slice()
46 题
记住最简单的框架
var permute = function(nums) {
let used = new Array(nums.length).fill(false)
let res = [], track = []
function backtrack(nums, track, used) {
if(track.length == nums.length) {
res.push([...track])
return
}
for(let i=0; i<nums.length; i++) {
if(used[i]) continue
track.push(nums[i])
used[i] = true
backtrack(nums, track, used)
track.pop()
used[i] = false
}
}
backtrack(nums, track, used)
return res;
};
无非是改改做选择的方式,排除不合法选择的方式而已。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
难度在于返回要求格式,文章的路径为二维数组,我使用一维代替。考验JS语法。对map方法的了解。
51题代码
var isValid = (row, col, track) => {
for(let i=0; i<row; i++) {
if(track[i]==col || Math.abs(track[i] - col) / (row - i) == 1) return false
}
return true
}
function transform(track) {
let n = track.length
let board = new Array(n).fill(0).map(() => new Array(n).fill('.'))
for(let i=0; i<n; i++) board[i][track[i]] = 'Q'
// 不会改变原始数组
return board.map((val) => val.join(""))
}
var solveNQueens = function(n) {
let res = [], track = []
function backtrack(track, row) {
// 不是n-1
if(row == n) {
res.push(transform(track))
return
}
for(let col = 0; col < n; col++) {
if(!isValid(row, col, track)) continue
track.push(col)
backtrack(track, row+1)
track.pop()
}
}
backtrack(track, 0)
return res;
};
文章总结
其实回溯算法其实就是我们常说的 DFS 算法,本质上就是一种暴力穷举算法
写 backtrack 函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。
有的时候,我们并不想得到所有合法的答案,只想要一个答案,怎么办呢?
第二个return,不在继续找「选择列表」
第三个return,「选择列表」中没有合适地进行下一步探索,告诉上一层失败

贪心——455. 分发饼干(简单)
算法小抄没有总结贪心算法,因为贪心没有套路,说白了就是常识性推导和举反例验证。
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。
之前的田忌赛马也属于贪心,870. 优势洗牌
455题代码
var findContentChildren = function(g, s) {
g.sort((a, b) => b - a) // 胃口
s.sort((a, b) => b - a) // 饼干
let res = 0, index = 0 // 饼干指针
for(let i=0; i<g.length && index<s.length; i++) {
if(g[i] <= s[index]) {
res++
index++
}
}
return res
};
376. 摆动序列 ()——贪心 或 动规


实例2整个序列的差值为(16,-12,5,3,2,-5,11,-8)
我都不知道代码随想录说的是啥。。。看leetcode别人的讲解

7.因为一段相邻的相同元素中我们最多只能选择其中的一个,所以我们可以忽略相邻的相同元素。
8.对于序列中既非「峰」也非「谷」的元素,我们称其为「过渡元素」。如序列 [1,2,3,4][1,2,3,4] 中,22 和 33 都是「过渡元素」。
贪心算法
了解概念后,好像是在找数学上的极值。然后莫名地变成了大小为3的滑动窗口。
报错案例:
[0,0]
1
报错案例:
【4,2,2,4】如果每次都更新左右差值,会忽略了2这个极小值。所以是双指针,非滑动窗口。
报错案例:
[1,1,1,2,2,2,1,1,1,3,3,3,2,2,2]
如果rightDiff非0,leftDiff 就要取反继承它,因为我是用中间的数减两边。
如果rightDiff为0,就是走向平面,leftDiff保留上一次的坡度。
最后边界情况,防止最后rightDiff一直是0,那么一直没找到极值,那么最右边也被忽略了。方法就是,看leftDiff如果有坡度,则最右边也是极值。
因为最左边肯定算一个,就看最右边。
var wiggleMaxLength = function(nums) {
if(nums.length == 1) return 1
let leftDiff = nums[1] - nums[0], rightDiff = 0, res = 0;
for(let i = 1; i<nums.length - 1; i++) {
rightDiff = nums[i] - nums[i+1]
if(leftDiff * rightDiff > 0) {
res++
}
if(rightDiff) leftDiff = -rightDiff
}
board = leftDiff ? 2 : 1
return res + board
};
动态规划算法
动规也不会呀。。。还是要了解山峰和山谷这个概念
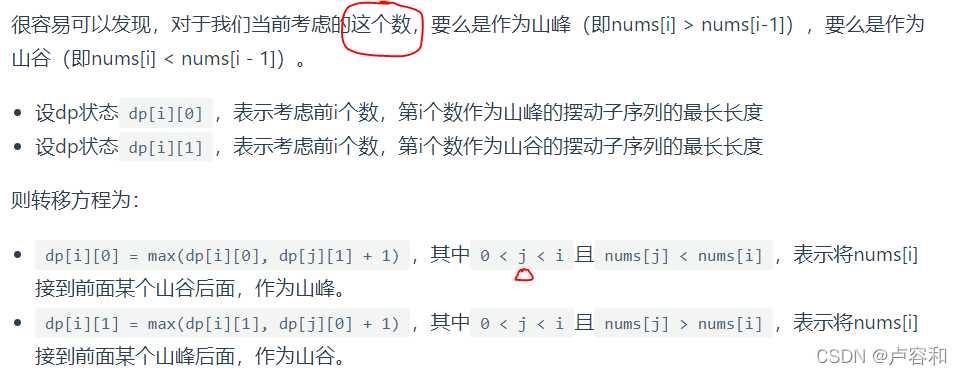
一看解释就觉得很简单,因为动态规划难在:定义数组含义和状态转移方程。
初始化:认为最左边认为是一个极值,可以是极大值也可以是极小值,最右边则不一定。
状态方程:可看到如果与前一个节点值相同,则不处理该节点
var wiggleMaxLength = function(nums) {
let n = nums.length
if(n == 1) return 1
const dp1 = new Array(n).fill(1) // 山峰
const dp2 = new Array(n).fill(1) // 山谷
for(let i=1; i<n; i++) {
for(let j=0; j<i; j++) {
if(nums[j] > nums[i]) dp2[i] = Math.max(dp2[i], dp1[j]+1)
if(nums[j] < nums[i]) dp1[i] = Math.max(dp1[i], dp2[j]+1)
}
}
return Math.max(...dp1, ...dp2)
};
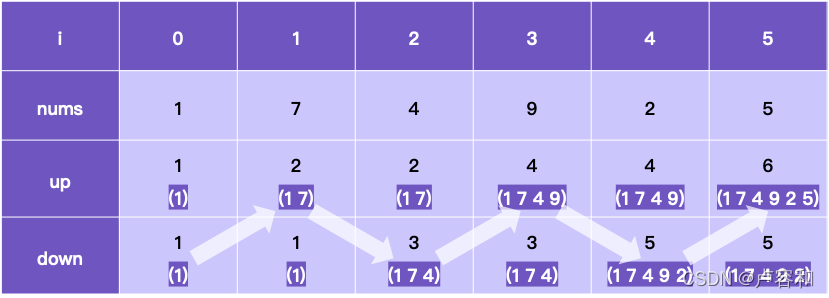
保存山峰和山谷的最大值,则dp转移方程中就没有必要j从0遍历到i-1
还是上面好理解,这个简化也是试出来的。或者说明与当前山谷最近的山峰肯定节点更多。
var wiggleMaxLength = function(nums) {
let n = nums.length
if(n == 1) return 1
let dp1 = 1 // 山峰
let dp2 = 1 // 山谷
for(let i=1; i<n; i++) {
if(nums[i-1] > nums[i]) dp2 = dp1+1
if(nums[i-1] < nums[i]) dp1 = dp2+1
}
return Math.max(dp1, dp2)
};
