[数据结构与算法][ZJOI2010] 贪吃的老鼠（二分+差分+神仙建图网络流）

problem

luogu-P2570

solution

卧槽网络流尼玛神题

首先这个最小延长时间 $T$ ，套路地考虑二分，将问题转化为判定性问题。

其次 $n,m$ 和奶酪存在时间 $[l,r]$ 的量级差很大，我们肯定会猜想一段时间内选择吃奶酪的老鼠是一样，套路地考虑离散化。

将 $n$ 个奶酪的出现、消失时间放进时间轴 $ti[]$ 中。

有序化，将时间轴割裂成若干段不相交且并集为全集的的小区间，一段时间一段时间地考虑。

像这种贪心贪不动，$dpp$ 不动的题目，我们就可以往网络流上靠了 。

其实是感觉是个网络流那它多半就是网络流。

现在就当大家已经想(猜)到这是道网络流了。

这道题问题就在于如何建立一个和原问题等价的网络流。

满足：任一时刻，一只老鼠最多吃一块奶酪，一块奶酪最多被一只老鼠吃。

因为网络流是同时多路径流，所以我们很难在网络流上面直观理解一对一。

本版块是对建图的描述。

刚开始，很容易想到。$s,t$ 源汇点，$1～n$ 的奶酪，源点 $s$ 分别与这 $n$ 块奶酪连边，容量为对应奶酪的大小 $p$。

然后后面就开始 尼玛 神起来了。

• 首先要将老鼠按吃的 速度从大到小 排序，最后面插个速度 $0$，再 差分 一下，得到新的速度序列 { v } \{v\} {v}。

  $\text{e.g.}:5429\to 95420\to 4122$。

  后面建图部分的第 $i$ 个老鼠点若未明确指出原老鼠 / 差分老鼠，则均指已经差分后的第 $i$ 个老鼠点。

差分过后，按划分的每个时间段重复以下的操作：

假设这个时间段 $j$ 的长度为 $time=ti[j+1]?ti[j]$。

• 枚举 $1～m$ 老鼠，给其一个新编号 $tot++$，与汇点连边。

  第 $i$ 个老鼠连边容量为 $v_i?i?\text{time}$。

  你肯定会疑惑这个容量太奇怪了。但先别着急。

  看图：

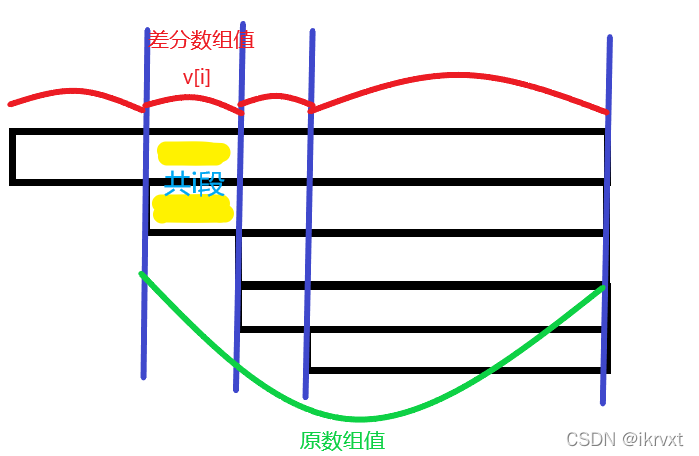
  $v_i?i:$ 差分值乘上它的差分数组内的编号。

  我们观察得到，假设差分数组为 $d$，原数组为 $o$，则有 $\sum d_i?i=\sum o_i$。

  那么乘上 $time$ 就是这个老鼠点在这个时间段能吃的奶酪限制。

  这个差分相当于将原老鼠切成了若干块，按相同块分类合并。

  这个在差分数组内的编号 $i$ 意思就是有 $i$ 只原老鼠能划分出这个 $v[i]$ 块，统称一只差分老鼠。

• 枚举 $1～n$ 奶酪，对完全在这个时间段出现的奶酪继续操作：

  与每个老鼠连边，容量 $v_i?time$。

  表示一只老鼠最多在一块奶酪上付出的努力。

  看图：

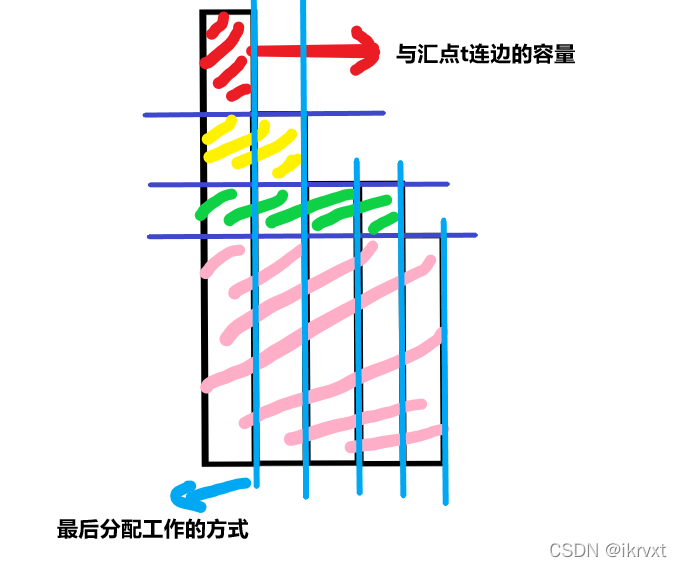
你可以将不同颜色的蓝线当作坐标轴的 $x,y$ 基准轴，然后划分出每个速度老鼠小方格，一个小方格一个小方格地分配。

从上往下从左往右第 $(x,y)$ 的方格可以理解为该时间段会有第 $y$ 只原老鼠吃掉第 $x$ 个奶酪的 $v_y?time$ 大小的部分。

每个奶酪会分配到某些行中的一个小方格，然后拼凑出来，相当于是吃掉了这个奶酪的一部分。

本板块是证明此种 奇怪神奇但是对的 网络流建图方式不会出现不合法的情况，即不存在某一时刻一只老鼠同时吃多个奶酪 / 一个奶酪同时被多只老鼠吃。

PS：本版块若未强调差分老鼠，则均指是原老鼠。

• 先证明不存在一只老鼠同时吃多个奶酪的情况。

  假设排序后第 $k$ 只老鼠在该时间段吃了 $x$ 块奶酪，第 $i$ 块奶酪吃了时间 $t_i$。

  如果 $(\sum t_i)>time$，则表示存在一只老鼠同时吃多个奶酪（不合法）。

  首先第 $k$ 个差分老鼠至少产生的流量都是 $(\sum t_i)?v_k$，而容量为 $v_k?k?time$。

  此时有两种情况：

  • 有速度更快的老鼠能够帮吃超额部分（引起老鼠必须同时吃奶酪的部分），那么就可以分担。

    就不会存在 $(\sum t_i)>time$。（也就是说看似不合法的流法可以通过调整变成合法流法）

  • 不能帮吃完所有超额部分。那么这些更快的老鼠肯定是吃过了，也就是它们在这个时间段每时每刻都在吃。

    在差分上会体现成前 $k?1$ 个差分老鼠对 $k$ 差分老鼠造成流量负担，加上原本流量，$(\sum t_i)?v_k+(k?1)?v_k?time=k?v_k?time+v_k?((\sum t_i^{\prime })?time)>k?v_k?time$，即流量大于容量，显然不可能，所以在网络流图上不可能跑成这样。（如果调整不了那么一开始就不可能跑成这种情况）

• 再证明不存在一个 $i$ 奶酪同时被多只老鼠吃的情况。

  假设有 $x$ 只老鼠吃了该奶酪，吃了时间 $t_i$。

  如果 $(\sum t_i)>tim$ 则表示存在一个奶酪同时被多只老鼠吃。

  由于排名靠前的老鼠会对排名靠后的老鼠造成影响。即吃了同一个奶酪的 排名最后面的 老鼠流量为 $(\sum t_i)?v_k>t_i?v_k$（奶酪向每个差分老鼠的连边容量）。

  也不存在跑出这种情况的可能。

在建图板块，是从差分到原来；而在证明板块，是从原来到差分。可多思考一下。

因为这个建图是差分后的建图，所以如果要输出方案（即还原每只老鼠吃的时间）很有可能遇到差分还原后某只老鼠的时间是负数。
还原方法就是第一只差分老鼠的流量 $/v$ 就是时间，然后把编号比它大的所有差分老鼠减去这个老鼠造成的流量贡献，以此类推。
网络流的流法很多种，我们只是知道最后流满没有。所以有可能某种流法看上去是不对的，但是它一定可以被调整成一种合法流法（优先满足编号小的差分老鼠）。
所以考察输出方案的话就显得不可做了。

code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 100000
#define maxm 500000
#define eps 1e-6
#define inf 1e9

int s, t, cnt, T, n, m;
int head[maxn], cur[maxn], dep[maxn];
struct edge { int to, nxt; double flow; }E[maxm];
namespace NetworkFlow {
    queue < int > q;
    void init() { s = 0, t = n * m * 2 + 1, cnt = -1, memset( head, -1, sizeof( head ) ); }
    void addedge( int u, int v, double w ) {
        E[++ cnt] = { v, head[u], w }, head[u] = cnt;
        E[++ cnt] = { u, head[v], 0 }, head[v] = cnt;
    }
    bool bfs() {
        memset( dep, 0, sizeof( dep ) );
        memcpy( cur, head, sizeof( head ) );
        dep[s] = 1; q.push( s );
        while( ! q.empty() ) {
            int u = q.front(); q.pop();
            for( int i = head[u];~ i;i = E[i].nxt ) {
                int v = E[i].to;
                if( ! dep[v] and E[i].flow > eps ) {
                    dep[v] = dep[u] + 1;
                    q.push( v );
                }
            }
        }
        return dep[t];
    }
    double dfs( int u, double cap ) {
        if( u == t or cap < eps ) return cap;
        double flow = 0;
        for( int i = cur[u];~ i;i = E[i].nxt ) {
            int v = E[i].to; cur[u] = i;
            if( dep[v] == dep[u] + 1 ) {
                double w = dfs( v, min( cap, E[i].flow ) );
                if( w < eps ) continue;
                E[i ^ 1].flow += w;
                E[i].flow -= w;
                flow += w;
                cap -= w;
                if( cap < eps ) break;
            }
        }
        return flow;
    }
    double dinic() {
        double ans = 0;
        while( bfs() ) ans += dfs( s, inf );
        return ans;
    }
}

struct node { double p, l, r; }c[maxn];
double v[maxn], ti[maxn];
double sum;
bool check( double delta ) {
    NetworkFlow :: init();
    for( int i = 1;i <= n;i ++ ) {
        NetworkFlow :: addedge( s, i, c[i].p );
        ti[i] = c[i].l, ti[i + n] = c[i].r + delta;
    }
    sort( ti + 1, ti + (n << 1 | 1) );
    int tot = n;
    for( int i = 1;i <= m;i ++ )
        for( int j = 1;j < (n << 1);j ++ ) {
            if( ti[j + 1] - ti[j] < eps ) continue;
            tot ++, NetworkFlow :: addedge( tot, t, ( ti[j + 1] - ti[j] ) * v[i] * i );
            for( int k = 1;k <= n;k ++ )
                if( c[k].l <= ti[j] and  ti[j + 1] <= delta + c[k].r )
                    NetworkFlow :: addedge( k, tot, ( ti[j + 1] - ti[j] ) * v[i] );
        }
    return sum - NetworkFlow :: dinic() < eps; 
}

signed main() { 
    scanf( "%lld", &T );
    while( T -- ) {
        scanf( "%lld %lld", &n, &m );
        for( int i = 1;i <= n;i ++ ) 
            scanf( "%lf %lf %lf", &c[i].p, &c[i].l, &c[i].r );
        sum = 0; 
        for( int i = 1;i <= n;i ++ ) 
            sum += c[i].p;
        for( int i = 1;i <= m;i ++ ) 
            scanf( "%lf", &v[i] );
        sort( v + 1, v + m + 1, []( int x, int y ) { return x > y; } ); 
        for( int i = 1;i < m;i ++ ) 
            v[i] = v[i] - v[i + 1];
        double l = 0, r = 5e7, ans;
        while( l + eps < r ) {
            double mid = ( l + r ) / 2;
            if( check( mid ) ) ans = mid, r = mid;
            else l = mid;
        }
        printf( "%.4f\n", ans );
    }
    return 0;
}