二叉查找树
问题引入?
二叉查找树:相比哈希表,二叉查找树有什么优势?
二叉查找树:一种具有特殊功能的二叉树
二叉查找树中的任意一个节点,其左子树中的每个节点的值都要小于这个节点的值,而右子树中每个节点的值都要大于这个节点的值。 基于这种特殊的结构,可以进行快速查找。
我们知道,哈希表也支持数据的快速插入、删除和查找操作,并且这三个操作的时间复杂度都为O(1)。既然有了这么高效的哈希表,那么在所有用到二叉树的场景中是不是都可以替换或使用哈希表呢?哪些场景不适合哈希表,必须要用二叉查找树来实现呢?
二叉查找树的操作
1、查找
通过节点的大小比较进行查找。
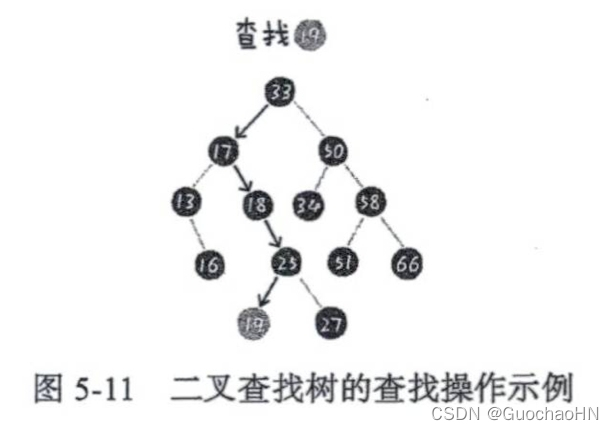
2、插入操作
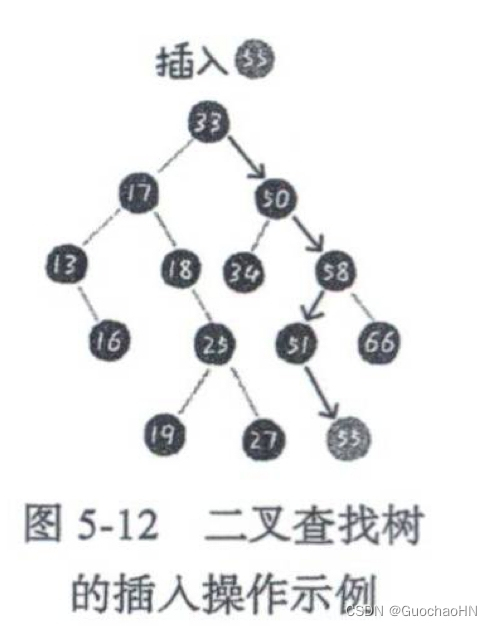
3、 删除
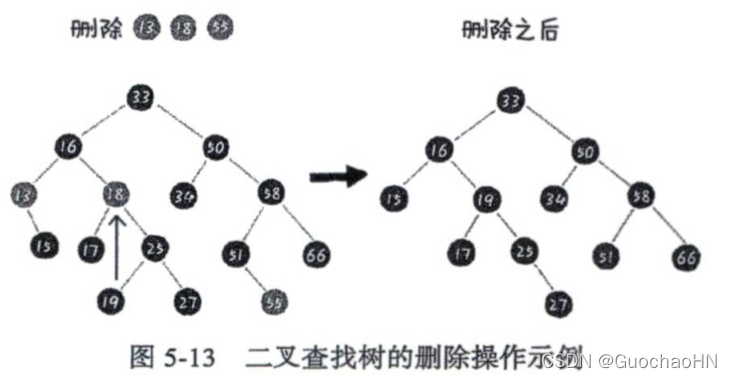
性能分析
对于同一组数据,我们可以构建各种不同的二叉查找树,如图所示,因此插入、删除和查找操作的执行效率也不同,在最糟糕情况下,根节点的左右子树极度不平衡,已经退化为了链表,因此,查找的时间复杂度就变成了O(n)。在理想情况下(二叉查找树为满二叉树),查找的时间复杂度为O(logn)。

总结
哈希表的插入、删除和查找操作的时间复杂度都是常量级的,非常高效。而二叉查找树在比较平衡的情况下各种操作才满足O(logn)。相对哈希表,二叉树好像并没有优势。
现在来回答开篇的问题:
在所有用到二叉树的场景中是不是都可以替换或使用哈希表呢?哪些场景不适合哈希表,必须要用二叉查找树来实现呢?
哈希表并不能替代二叉查找树
第一:哈希表中的数据是无序存储的,如果要输出有序数据序列,需要先进行排序,或者配合有序链表来使用。而对于二叉查找树,我们只需要进行中序遍历,就可以在O(n)的时间复杂度内,输出有序数据序列。
第二:哈希表扩容耗时很多,而且当遇到哈希冲突时,性能不稳定。而对于二叉查找树,如果用平衡二叉树就非常稳定,时间复杂度稳定在O(logn)。后文将介绍。
第三:O(logn)的算法并不一定比O(1)的算法运行速度慢。尽管哈希表上操作的时间复杂度是常量级的,但因为哈希冲突的存在,再加上哈希函数的计算耗时,哈希表并不一定就比平衡二叉树效率高。
第四:哈希表的构造比二叉查找树复杂,需要考虑的东西很多,如哈希函数的设计、冲突解决方法、扩容和缩容等。平衡二叉树只需要考虑如何维护平衡性。
平衡二叉查找树
上文讲到,二叉查找树在频繁的动态更新的过程中,可能会出现树的高度远大于logn的情况,即退化为链表,时间复杂度变为O(n)。要解决性能退化问题,就需要用到平衡二叉查找树。
平衡二叉树:二叉树中任意一个节点的左右子树的高度相差不能大于1,且满足二叉查找树的特点(其左子树中的每个节点的值都要小于这个节点的值,而右子树中每个节点的值都要大于这个节点的值)。
基于定义,我们不难理解,为什么平衡二叉查找树可以解决性能退化问题,因为整棵树尽可能的“矮胖”,而非“高瘦”,能让整棵树的高度相对来说低一些。在多次插入和删除过后,通过对树进行平衡性维护,显然也不会出现退化成链表的情况。始终保持树的高度为logn。
红黑树
平衡二叉树有很多,但一提到平衡二叉树,常常提及的就是红黑树。
红黑树是一种相对平衡的二叉查找树,不符合严格意义上平衡二叉查找树的定义。
顾名思义:有两类节点,黑色和红色。
必须满足一下四个要求:
根节点是黑色。
叶子结点是黑色,且不存储数据。
红色节点被黑色节点隔开。不能相邻。
对于每个节点,从该节点到其叶子节点的所有路径,都包含相同数目的黑色节点。
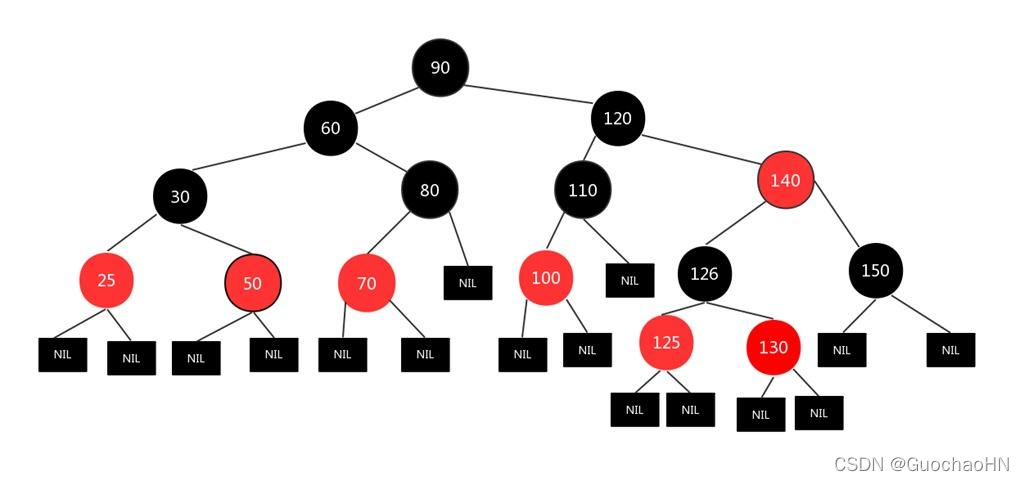
那么如何证明红黑树是近似平衡的呢?
只需证明红黑树的高度近似logn就可以了。
1、将所有的红色节点从树中去掉,并把这些没有父节点的节点悬挂在祖父节点。如下例图:二叉树变成了四叉树
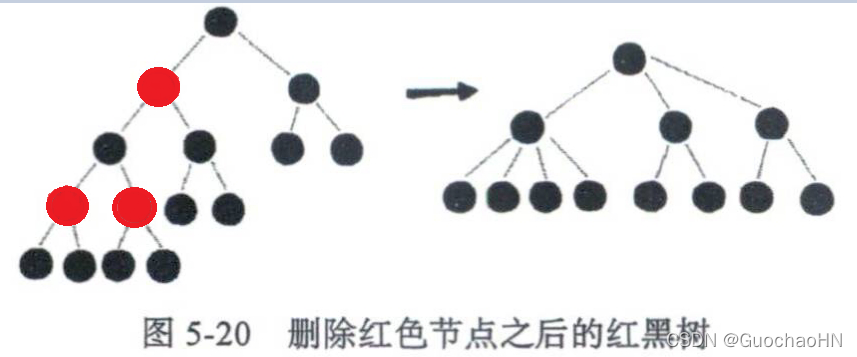
2、从只包含黑色节点的四叉树中取出某些节点,放到叶子节点的位置,四叉树就变成了完全二叉树(根据红黑树的定义:从任意节点到其叶子节点的每个路径都包含相同数目的黑色节点。)
3、因此,仅包含黑色节点的四叉树的高度比包含相同节点个数的完全二叉树的高度还要小。所以去掉红色节点的的红黑树的高度一定小于logn。
4、将红色节点加回去,因为红色节点不能上下相邻,所以在任意一条路径上,黑色节点的数量一定不必红色节点少,所以加入红色节点之后,红黑树的高度不超过2logn。即可证红黑树是近似平衡的。
为什么红黑树如此的受欢迎?
AVL树是一种高度平衡的二叉树,查找数据的效率非常的高,但是,AVL树为了维护这种高度的平衡,需要付出更多的代价。为了维护平衡性,每次插入、删除数据都要对树中节点的分步做调整,操作耗时、复杂。
红黑树只做到了近似平衡,并没有做到严格定义上的平衡,因此,维护平衡性的成本比AVL树要低。更加重要的一点,大部分编程语言提供了封装了红黑树实现的类,我们直接拿来用即可,不需要从零开始实现,大大节省了开发时间。