学不可以已--------------------------------------------------博主:mx?
基础知识:
这个部分简单介绍一下辐射度量学的基础概念,这个部分的中文翻译比较多,尽量在英文语境下理解
Radiance:
辐射率/辐亮度,指的是单位投影面积、单位立体角上的辐射亮度
Irradiance:
辐照度,指单位面积接收到的辐射通量
Radiant flux:
辐射通量,又称辐射功率,指单位时间内通过某一截面的辐射能量
Radiant Intensity:
辐射强度,表示的是在单位球面上,一个光源向每单位立体角所投送的辐射通量。
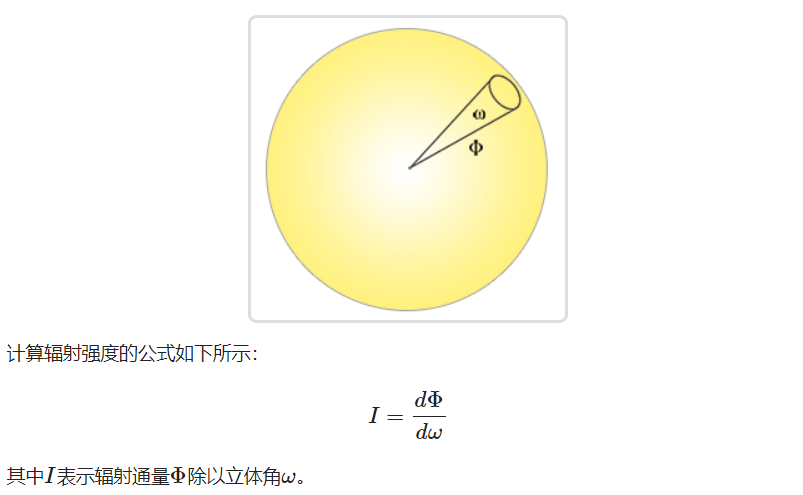
Solid Angle:
立体角,可以为我们描述投射到单位球体上的一个截面的大小或者面积。投射到这个单位球体上的截面的面积就被称为立体角
Lambertian surface:
一种理想的漫射面,它所有方向的反射能量都相等,是指在一个固定的照明分布下从所有的视场方向上观测都具有相同亮度的表面,朗伯表面不吸收任何入射光.
Lambertian reflectance:
也叫理想散射或朗伯散射,不管照明分布如何,朗伯表面在所有的表面方向上接收并发散所有的入射照明,结果是每一个方向上都能看到相同数量的能量。
渲染方程:
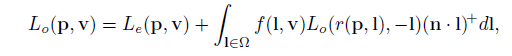
我们先来看右半部分的渲染方程
反射方程:
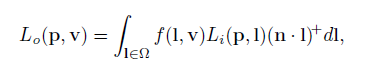
其中L0(p,v)表示的是从物体表面位置p输出的Radiance,v为视角方向,Ω为p点法线所在的半球,l是光线方向,n是p点法线,f(l,v)为BRDF,Li(p,l)表示的是从光线方向输入到p点的Radiance,n·l就是法线和光线方向的点乘,并且如果是复数会规范到0
其中的Li(p,l)可以替换成
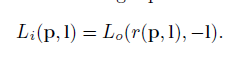
对于这个替换的公式我觉得可以先看这个示意图
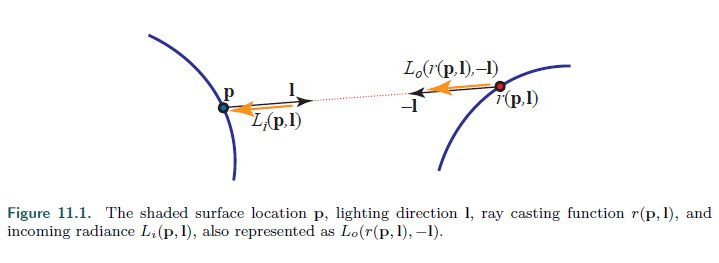
这个表示的是从光线方向l输入到表面点p的Radiance其实也是等于其他点(这个点就从点p和原本的光线方向l发出去击打到的其他表面点)发出的,r(p,l)就是ray castiing function(路径追踪方程),用来求出从点p和原本的光线方向l发出去击打到的其他表面点。并且易知这个方程可以是个无穷递归方程
自发光(Emitted)方程:
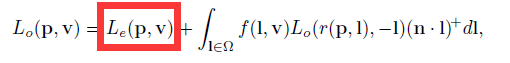
表示的是从物体表面p点从视角方向v发射出去的Radiance
照明问题建模:
在实时渲染中,我们通常为了优化性能,会只在局部空间中进行计算光线的弹射。(像透明、反射、阴影这些一般依然使用全局光照算法,因为他们需要的信息不仅仅是被照亮的物体)。
Heckbert创建了一种用来模拟路径光照的方案。
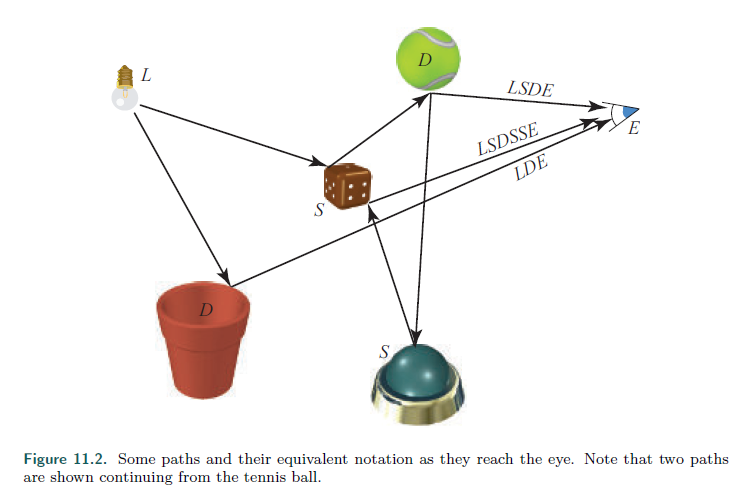
在这种方案中,光线为L,眼睛为E,漫反射为D,高光反射为S,还有一个相关的其他符号表格
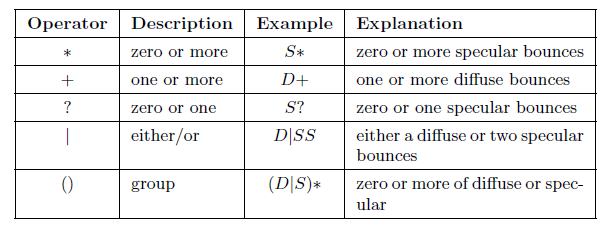
渲染方程本身可以简化为L(D|S)?E
--------------------------------------------------博主:mx?
全局照明研究的重点是计算沿这些路径的光传输的方法。当将其应用于实时渲染时,我们常常愿意牺牲一些质量或正确性来进行有效的评估。最常见的两种策略是简化和预计算。例如,我们可以假设在到达眼睛之前所有的反射光线都是漫反射的,这种简化在某些环境中很有效。我们还可以预计算一些关于对象间效果的离线信息,例如生成纹理,记录表面上的光照水平,然后实时执行依赖于这些存储值的基本计算。
通用全局光照:
这里主要介绍两种方案来实现渲染方程,一种是finite element methods(有限元法),一种是蒙特卡洛积分。在Radiosity(辐射着色)着色中我们通常使用第一种方法,而在光线追踪中通常采用蒙特卡洛积分。
Radiosity(辐射着色):
Radiosity主要是用来模拟漫反射表面之间的反射光,他的名字来源于他算法计算出来的量。
基本思想:
基本思想是在稳定状态下,每个表面都可以被看作是一个光源,并且基本的辐射着色算法做了一个假设:所有的间接光照都来源于漫反射表面。这个假设不适用于光滑的表面,比如抛光的大理石或者镜子,但是对建筑来说一般适用。这个方法的符号表示就是LD*E 。
并且Radiosity假设表面是由一定数量的小块组成,对于每个小块会单独计算,然后再取平均(为了精度需要划分的小块足够小,数量足够多)
再看公式:
我们从渲染方程出发,每个小块的Radiosity可以从以下方程中推出
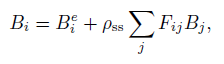
Bi就算每个小块求出来的结果,

是辐射出射度(自己发出来的,或者说这个小块原本就有的),Pss是次表面散射率[有多少能量被吸收,多少被散射出去],Fij表示的是 i 这个小块和 j 这个小块之间的形状因数。
形状因数:
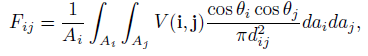
其中Ai表示的是 i 小块的区域,V(i,j)是i点和j点的可视度方程(有遮挡就是0,没有遮挡就是1),θ就是两个点相对于法线的角度,dij表示的是 i j 两点的距离
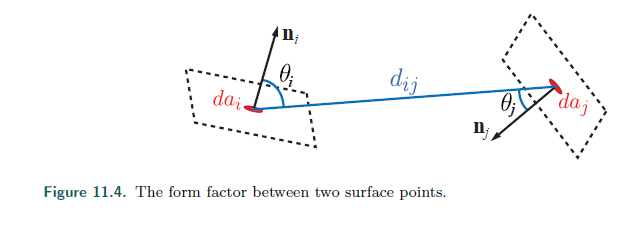
形状因数是一个纯几何项,表示的是i小块能够漫反射到j小块上的比例,两个小块之间的面积,角度,距离,以及他们之间任何表面都会影响他们的形状因子。
在Radiosity算法中准确的算出两个小块之间的形状因数很重要,但是由于小块数量的增加,会带来较高的计算复杂度,我们常常使用预计算形状因数的方法来减少复杂度
光线追踪:
基本思想:
光线追踪使用光线来确定不同场景元素之间的光传输。在最基本的形式中,光线从相机通过pixel网格发射到场景中。对于每条射线,找到最近的物体。然后,通过向每一盏灯发射一束光线,并找出两者之间是否有物体,来检查交点是否处于阴影中。不透明的物体挡住光线,透明的物体使光线减弱。其他射线可以从交点产生。如果一个表面是光滑的,一条射线就会在反射方向上产生。这条光线会拾取第一个相交物体的颜色,然后测试其交点的阴影。
蒙特卡洛积分与路径追踪:
蒙特卡洛方法是一类通过随机采样来求解问题的算法的统称,要求解的问题是某随机事件的概率或某随机变量的期望。通过随机抽样的方法,以随机事件出现的频率估计其概率,并将其作为问题的解。
在用来计算函数积分的时候,一般定义如下图:

(更加详细的证明这个公式的正确性的文章:蒙特卡洛积分 - 知乎)
蒙特卡洛积分有什么用呢,因为光线追踪的方程是递归的。这个就意味着对于每一条射线,我们都需要在不同的位置,再次求积分。并且直接通过解析式求定积分是十分困难的。这个时候我们就能够使用定积分来近似求解这个积分。采样点越多,精度越高。这就意味着只要有足够的时间我们就能够以更高的精度来计算这个积分。当我们发射射线时,我们对渲染方程的被积函数进行点采样。即使在交点处还有另一个积分要求值,我们不需要它的最终值,我们可以只对它再次点采样。当光线穿过场景时,就会形成一条路径。沿着每条路径传输的光提供了被积函数的一个计算。这个过程称为路径跟踪
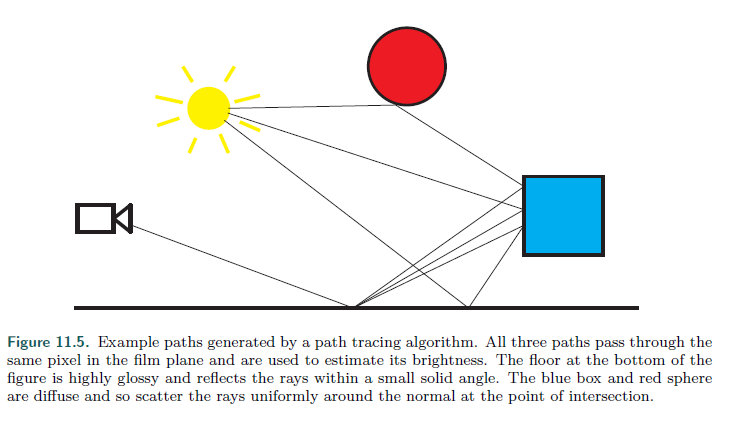
如果路径数过少就很容易出现噪声,并且我们一般采用重要性采样的方式来进行路径追踪,这个方法的思想就算我们通常生成更多能够射向光源的路径。
环境光遮蔽:
AO理论(Ambient Occlusion Theory):
环境光遮挡的理论可以从反射率方程推出来,我们首先可以关注Lambertian表面。这些表面的出射辐射度Lo与表面辐照度e成正比。辐照度是入射辐射度的余弦加权积分。一般来说,他取决于表面位置p和表面法线n,并且我们假设入射光对于任意入射方向l是恒定的Li( l )=LA,那么我们计算辐照度的公式为
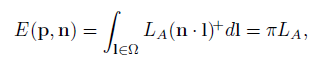
这个公式也是渲染方程中的积分的部分,只是没了BRDF。
因为现在还没有考虑任何遮挡,当我们考虑上遮挡公式就变成了
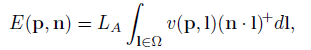
v(p,l)就是可见性方程,如果光线从p点的l方向被遮挡就是0,没有被遮挡就是1
现在这个方程有点像环境光遮蔽的方程了,能见度函数的归一化、余弦加权积分称为环境光遮蔽,其中LA=1/ㄇ
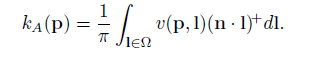
他的数学意义很简单,就是在半球上可见度百分比。将环境光遮蔽带入到辐照度的方程中就可以得到

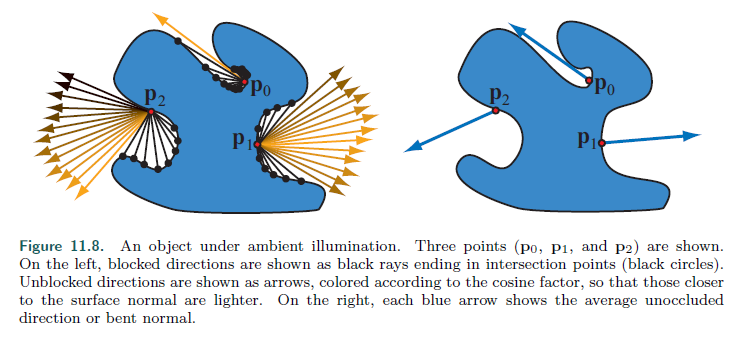
(上图,左边演示了环境光遮蔽,右边表示的是环境法线)
除了计算出环境光遮蔽系数KA,Landis还算出来了一个环境法线:
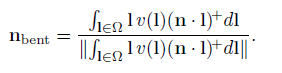
这个法线在计算着色的过程中比使用原本的几何法线会更加准确,因为考虑了环境的因素
可见性和遮蔽(Visibility and Obscurance):
对于计算机环境遮挡因子KA的可见性函数v(l)需要仔细定义。假如在物体表面直接投射无限远的射线,在封闭空间的物体达到的效果并不好,因为所有来自表面的光线都必然会被遮挡。
于是Zhukov等人引入了遮挡度的思想,将可见性函数v(l)替换为距离映射函数p(l),对环境光遮蔽计算进行了改进:
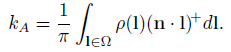
v(l)只有01两种指,而p(l)是一个连续的基于距离的函数,当相交距离为0时p(l)为0,当相交距离大于指定距离dmax或者根本没有相交的时候,p(l)为1。
唯一不太好的就是dmax需要手动指定,但是这个缺陷是可以接受的。
相互反射的计算(Accounting for Interreflections):
尽管环境光遮蔽产生的结果在视觉上令人信服,但它们比全局照明模拟产生的结果要暗。环境遮挡和全全局照明之间的区别的一个重要来源是相互反射。这种差异可以通过增加kA值来解决。使用模糊距离映射函数而不是可见性函数也可以缓解这个问题,因为对于阻塞的方向,模糊函数的值通常大于零。
但是我们还是想要模拟相互反射的计算结果。Stewart 和 Langer提出了一种快速的近似计算来模拟相互反射:
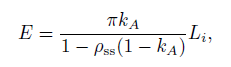
其中Pss是次表面散射率,并且我们使用了一个新的等式来改变KA项:
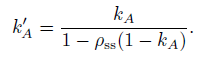
这个变换将使环境光遮蔽因子变亮,使其在视觉上更接近于一个完整的全局照明解决方案的结果,包括相互反射。这种效应高度依赖于pss的值。
--------------------------------------------------博主:mx?
预计算环境光遮蔽:
预计算任何与光照相关的信息的过程,包括环境遮挡,通常被称为烘烤。蒙特卡罗方法是预计算环境遮挡的最常用方法。投射光线并检查与场景的交点,并用数值方法计算KA。例如,我们随机选择N个方向,均匀分布在整个半球的N个方向上,沿着这些方向追踪射线。根据交集的结果,我们评估可见度函数v。然后可以计算出环境遮挡为
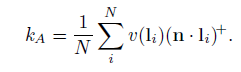
环境光遮蔽预计算可以在CPU或者GPU上执行,CPU常见的就是Embree方案,GPU常见的就是OptiX方案。
遮挡数据对于物体上的每个点都是唯一的。它们通常存储在纹理、体积或网格顶点中。不同的存储方法的特点和问题是相似的,无论存储的信号类型。同样的方法也可以用于存储环境遮挡、定向遮挡或预先计算的光照。这些数据有存储在cube map中的也可以存储在三维网格或者将计算的值存储在顶点中,然后通过插值来取值。
动态计算环境光遮蔽:
对于静态场景我们可以采用预计算出KA和环境法线nbent,然而对于动态物体和场景一般实时计算会取得更好的结果。
这个计算可以在模型空间,也可以在屏幕空间。离线计算环境光遮蔽的时候通常需要向场景投射大量的射线,并检查交点。实时的计算中一般没法这么多。
基于SDF的计算方法也能够得到不错的结果,Evans在一个体积纹理中为一个场景创建和存储了一个SDF。为了估计物体上某个位置的遮挡,他使用了一种启发式方法,将一些点的采样值结合起来,这些点沿着法线逐渐远离表面。
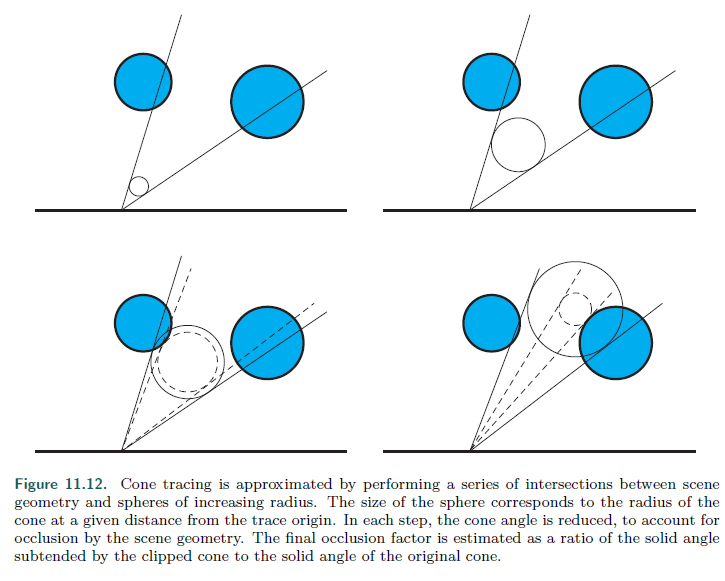
我们通过这张图来详细理解一下这种SDF的方法,球体的大小对应于从轨迹原点到给定距离的圆锥体的半径。在每一步中,考虑场景几何的遮挡,锥角减少。最终的遮挡因子估计为被裁剪锥所对的实心角与原始锥的实心角的比值。
而实时的游戏中一般是使用基于屏幕空间的环境光遮蔽。
SSAO:
基本流程:
最简单的基础形式是使用球形分布的采样点,在目标像素周围,视图空间内,在一定半径内的球行内部进行 N 几个采样点的采样,然后将采样点映射到屏幕空间,和 depth-buffer 中的深度进行比较,记深度测试通过(高于片段深度值样本)的点个数为 M,得到KA为
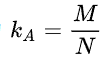
再考虑余弦权重(n·l),并且一般采样核心是一个半球体,因为使用球体的话,物体自己内部也会被采样到,会导致即使是平平的墙面也会灰蒙蒙的。
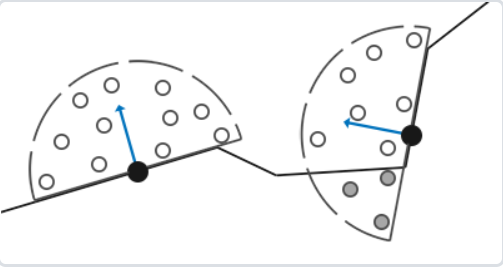
对于每一个片段,我们将需要这些数据:
- 逐片段位置向量
- 逐片段的法线向量
- 逐片段的反射颜色
- 采样核心
- 用来旋转采样核心的随机旋转矢量
由于SSAO是一种屏幕空间技巧,我们对铺屏2D四边形上每一个片段计算这一效果;也就是说我们没有场景中几何体的信息。我们能做的只是渲染几何体数据到屏幕空间纹理中,我们之后再会将此数据发送到SSAO着色器中,之后我们就能访问到这些几何体数据了。这和延迟渲染很相似。这也就是说SSAO和延迟渲染能完美地兼容,因为我们已经存位置和法线向量到G缓冲中了。
重建世界坐标:
如果我们只知道深度,怎么重建世界坐标呢,这个可以从当前的uv坐标反推出NDC坐标
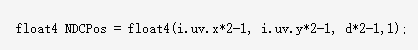
然后乘以View-Projection的逆矩阵,将NDC坐标转换到世界坐标系下,最终除以worldPos.w,就能得到准确的世界坐标。
这个的数学证明:从NDC(归一化的设备坐标)坐标转换到世界坐标的数学原理 - 爱码网
法向半球:
我们再来讲一下怎么使得采样的是一个半球:我们在切线空间中以-1.0到1.0为范围变换x和y方向,并以0.0和1.0为范围变换样本的z方向(如果以-1.0到1.0为范围,取样核心就变成球型了)。由于采样核心将会沿着表面法线对齐,所得的样本矢量将会在半球里。
切线空间:
那怎么转换到法线空间呢,这个很简单,和view矩阵一样,只需要知道在顶点处的Right,Up,Direction三个方向组合就能够得到变换的矩阵,因为原本的点已经和需要的原点一致就不需要平移过去了,Right,Up,Direction实际对应就是T(切线) B(副切线) N(法线)三个向量。
但是我们一般只知道点对应的法线。那怎么求法线副法线呢?我们首先知道一个特性就是法线贴图的切线和副切线和纹理坐标的两个方向是对齐的。看下面这个图:
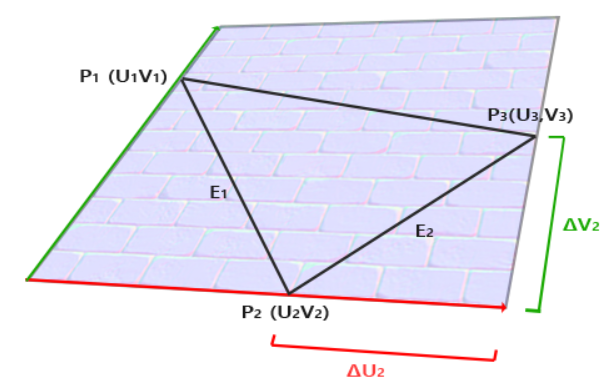
注意上图中边E2与纹理坐标的差ΔU2、ΔV2构成一个三角形。ΔU2与切线向量T方向相同,而ΔV2与副切线向量B方向相同。这也就是说,所以我们可以将三角形的边E1与E2写成切线向量T和副切线向量B的线性组合:
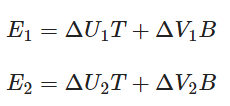
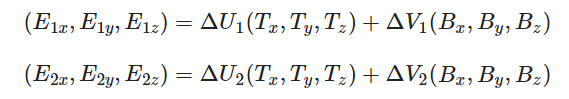
写成矩阵的乘法:
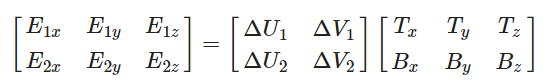
两边都乘以ΔUΔV的逆矩阵等于
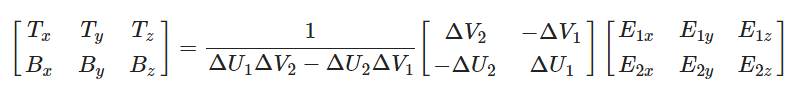
(逆矩阵求法大致是把它变化为1除以矩阵的行列式,再乘以它的伴随矩阵)
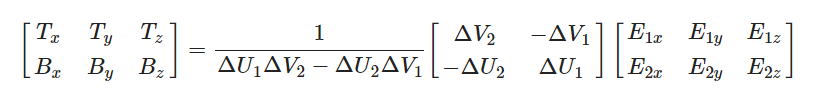
有了最后这个等式,我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量T和副切线B。
AO的渲染:
--------------------------------------------------博主:mx?
我们再来看反射方程
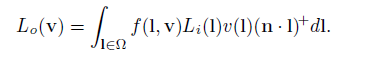
如果我们处理的是一个漫反射表面,那么其中的f(l,v)可以用Lambertian BRDF进行替换,就可以得到:
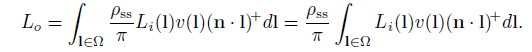
我们再对上面的式子进行替换:
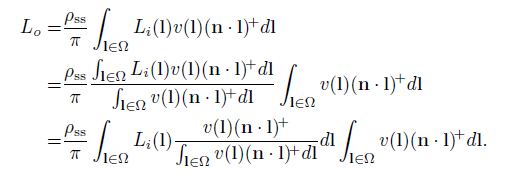
我们用如下这两个式子对上面这个式子进行替换
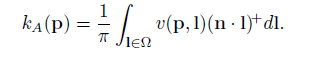
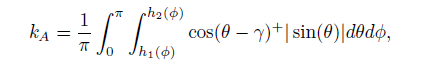
得到
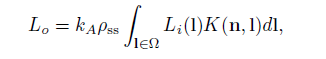
我们来看一下这个新的式子,这个新的式子对入射的辐射度应用了一个滤波核。滤波核K在空间和方向上都有复杂的变化,但它有两个重要的性质。首先,由于点积,它最多覆盖点p法线周围的半球。第二,由于分母中有标准化因子,它在半球上的积分等于1。为了进行着色,我们需要计算入射辐射度Li和滤波函数K的乘积的积分。我们对其简化一下,只使用余弦的滤波核H:
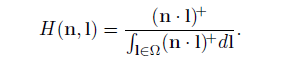
当没有任何东西阻挡入射光的时候,这种近似是正确的。这个时候公式变成了:
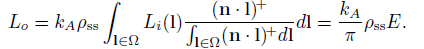
这意味着,在最简单的形式下,环境遮挡的阴影可以通过计算辐照度并乘以环境遮挡值来完成。
到现在为止,我们假设我们是在给朗伯曲面着色。当处理一个更复杂的非常数BRDF时,这个函数不能从积分中提取出来。对于高光材料,K不仅取决于可见性和法线,还取决于观察方向。对于环境地图的着色,Pharr提出了一种替代方法,使用GPU的纹理过滤硬件来动态执行过滤。滤波核K的形状是动态确定的。它的中心是弯曲法线的方向,它的大小取决于kA的值。这与公式中的原始滤波核更精确匹配。
定向遮蔽:
DO(Directional Occlusion)的理解:
我们先来理解一下DO大概是个什么意思和作用:
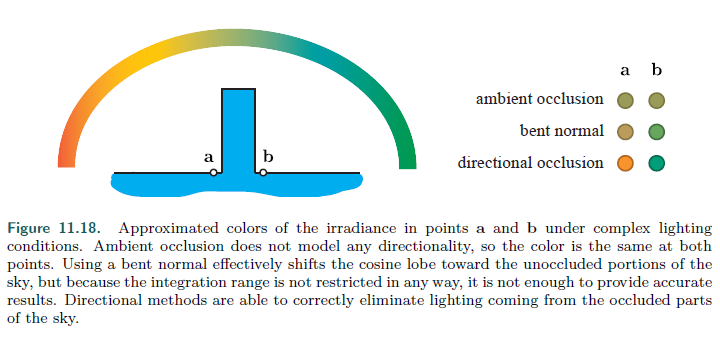
我们来看上面这张图,虽然环境光遮蔽提高了图形的视觉质量,但是这个模型并没有对方向光进行建模,也就说只使用AO的话即便环境光遮蔽会使得a点和b点变暗,但是他们仍然会被天空中的红色和绿色照亮,虽然使用环境法线可以缓解这种情况,但是并不完美。DO就是用于为大面积灯光或环境照明提供遮挡,他只需要编码光源的单个位置或者方向的可见性,在这种情况下,生成的阴影是柔和的。
预计算DO:
Max提出了一种在高度表面描述自遮挡的概念叫做视野采样( horizon mapping )。对于表面的每个点,视野的高度角是由一些方位角方向确定的,例如,8个方向:北、东北、东、东南、等等。
另一种方式是ambient aperture lighting,这个技术的存储需求比 horizon mapping 但当未包含的方向集不像椭圆或圆时,可能会导致不正确的阴影。
还有很多遮挡技术的变种。像Wang等人使用spherical signed distance function (SSDF)来表示可见度,它编码表示到球体上被遮挡区域边界的符号距离。就像环境遮挡一样,方向可见性信息可以存储在纹理、网格顶点或立方体中。
动态计算DO:
许多用于产生环境遮挡的方法也可以用来产生方向可见性信息:Ren等人的球谐函数和Sloan等人的屏幕空间变体以球面调和矢量的形式产生可见性。
或者是圆锥体追踪的方式,每个轨迹提供一个遮挡值,如果如果需要在特定方向上的可见性,我们可以追踪较少的圆锥体。
Iwanicki也使用圆锥体追踪,但他将其限制在一个方向上。结果被用来生成由近似于一组球体的动态角色投射到静态几何上的柔和阴影,类似于Ren等人[和Sloan等人。在这个解决方案中,静态几何图形的照明使用AHD编码存储。环境和方向组件的可见性可以独立处理。对环境部分的遮挡进行了解析计算。跟踪单个圆锥并与球体相交,计算方向分量的衰减因子。
许多屏幕空间方法也可以扩展以提供定向遮挡信息。Klehm等人使用z-buffer数据来计算屏幕空间弯曲锥,实际上是圆形孔径,很像Oat和Sander离线预计算的那些锥。当对一个像素的邻域进行采样时,它们将未包含的方向相加。得到的矢量的长度可以用来估计视锥的顶角,其方向定义了视锥的轴。Jimenez等人基于水平角估计锥轴方向,并从环境遮挡因子推导出角度。
DO的渲染:
我们再来考虑反射方程,这个版本中入射的辐射度被分成了远处的光Li和可见性v:
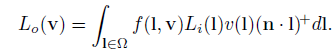
当我们在考虑一个准确的光线的时候,公式变成了这样:
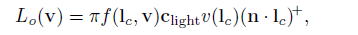
其中Clight是白Lambertian表面对着光反射的辐射度,lc是入射光的方向,我们可以将上面的方程解释为计算材料对无遮挡光的响应,并将结果乘以可见性函数的值。如果光的方向落在horizon以下(使用horizon mapping时),可见度锥外(使用环境孔径照明时),或在SSDF的负区域,能见度函数等于零。
我们可以对区域灯进行类似的推理。除了在光的立体角内它等于光源发出来的辐射度,其他地方Li处处等于零。我们称它为Li,并假设它在光的立体角上是恒定的。我们可以将整个球面的积分Ω替换为光的立体角的积分Ωl:
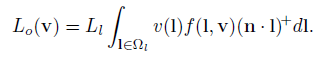
我们假设是在Lambertian表面,BRDF是恒定的,式子可以变化为:
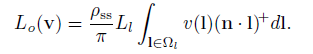
为了确定遮挡光线,我们需要计算可见度函数乘以余弦项在光线对着的立体角上的积分。为了确定遮挡光线,我们需要计算可见度函数乘以余弦项在光线对着的立体角上的积分。假设余弦项的值在整个积分域中是恒定的。如果光的面积很小,这个近似是相当精确的。为了简单起见,我们可以使用沿区域光中心方向计算的余弦值。这样我们就得到了可见光项对光的立体角的积分。我们选择如何继续,再次,取决于我们的能见度表示和区域光类型的选择。如果我们用球形光和视锥表示,那么积分的值就是视锥和光对着的视锥相交的立体角。可以用解析的方法来计算,如Oat和Sander所示。虽然精确的公式很复杂,但它们提供了一个在实践中行之有效的近似。如果可见性用球面谐波编码,积分也可以解析计算。对于环境照明,由于光照来自四面八方,不能限制其集成范围。我们需要找到一种方法来计算公式的完整积分。让我们先考虑Lambertian BRDF:
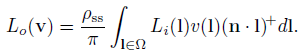
我们再变化一下:
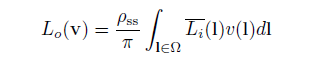
或者:

其中:
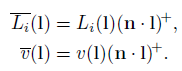
我们先用Li或者vi乘以cos。这样做使得被积函数只成为两个函数的乘积。虽然这看起来像是一个数学技巧,但它极大地简化了计算。如果用标准正交基(如球面谐波)表示因子,则二重积积分可以简单地计算出来。它是它们的系数向量的点积。我们仍然需要计算Li(l)或v(l)但因为它们包含了余弦,这比完全一般的情况更简单。如果我们用球谐函数,余弦投影到带谐函数(ZH),这是球谐函数的子集,每个波段只有一个系数是非零的。这个投影的系数有简单的解析公式。一个SH和一个ZH的乘积比一个SH和另一个SH的乘积计算效率高得多。
在运行时计算产品的计算成本很高。Iwanicki和Sloan描述了如何降低这种成本。在这种情况下,可以在较低粒度的顶点上计算产品。结果与余弦项卷积,投影到一个更简单的表示(AHD),然后插值和重构与逐像素法线。这种方法允许他们在要求60 FPS的游戏中使用这种方法。
Klehm等人提出了一种用环境地图表示的照明和用圆锥编码的能见度的解决方案。他们用不同大小的核来过滤环境地图,这些核代表了不同圆锥开口的可见性和照明的整体产品。它们在纹理的mip级别中存储增加锥角的结果。这是可能的,因为大锥角的预过滤结果在球体上变化平稳,不需要以高角度分辨率存储。在预滤波过程中,他们假设可见锥的方向与法线对齐,这是一种近似,但在实践中给出了可信的结果。
如果我们处理的是高光的brdf和环境照明,情况就更加复杂了。我们不能再从积分下提取BRDF,因为它不是常数。为了解决这个问题,Green等人建议用一组球形高斯函数来逼近BRDF本身。这些是径向对称函数,可以用三个参数来表示:方向(或均值)d,标准差p和振幅w。近似的BRDF被定义为球面高斯函数的和:
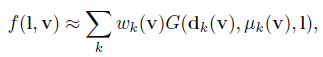
其中G(d, p, 1)为第k个叶值中的wk,沿d方向,具有锐度μ。对于各向同性BRDF,叶的形状只取决于法线方向和视点方向之间的夹角。近似值可以存储在一维查找表中并进行插值。根据这个近似,我们可以将等式写成:
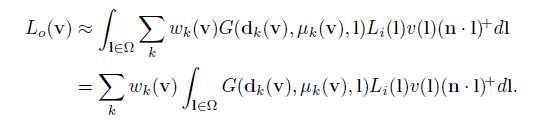
Green等人还假设可见函数在每个球面高斯函数的整个支持下都是恒定的,这使得他们可以将其从积分下拉出来。他们评估了叶中心方向上的能见度函数:
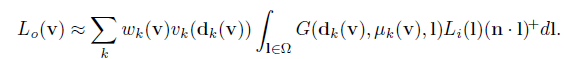
剩下的积分表示入射光与一个给定方向和给定标准差的球形高斯光卷积。这种卷积的结果可以预先计算并存储在环境映射中,较大的μ的卷积存储在较低的mip级别中。可见性用更低的球形谐波进行编码,但也可以使用任何其他表示,因为它只是点求值。
对于某些应用来说,从预过滤的环境地图中获取多个样本的方法可能过于昂贵。纹理采样通常已经成为渲染过程中的瓶颈。Jimenez等人和El Garawany提出了更简单的近似。为了计算遮挡因子,它们用一个锥代表整个BRDF叶,忽略了其对视角的依赖,只考虑材料粗糙度等参数。他们把可见度近似为一个锥,然后计算可见度和BRDF锥相交的立体角,就像环境孔径照明一样。用标量结果对光照进行衰减。尽管这是一个重要的简化,结果是可信的。
--------------------------------------------------博主:mx?
学习资料:
核心:《Real-Time Rendering》 Chapter 11 Global Illumination
2.【《Real-Time Rendering 3rd》 提炼总结】(八) 第九章 · 全局光照:光线追踪、路径追踪与GI技术进化编年史 - 知乎
4.从NDC(归一化的设备坐标)坐标转换到世界坐标的数学原理 - 爱码网
--------------------------------------------------博主:mx?