一、问题描述
??对于笛卡尔空间的参数化路径(如贝塞尔曲线、B样条曲线等)的速度规划问题,由于通常给定的是线速度 v v v、线加速度 a a a等,因此,若对参数化路径标量 s ∈ [ s m i n , s m a x ] s\in[s_{min},s_{max}] s∈[smin?,smax?]做速度规划,则首先必须将线速度、线加速度分别转化为参数化路径标量的速度、加速度。
二、简单推导
??设三维空间任一参数化路径为:
p
(
s
)
=
[
x
(
s
)
,
?
y
(
s
)
,
?
z
(
s
)
]
T
,
s
∈
[
s
m
i
n
,
s
m
a
x
]
(1)
p(s)=[x(s), \ y(s), \ z(s)]^T, s\in[s_{min},s_{max}]\tag{1}
p(s)=[x(s),?y(s),?z(s)]T,s∈[smin?,smax?](1)
??式(1)对时间
t
t
t求导得到分速度:
{
d
x
d
t
=
d
x
d
s
d
s
d
t
=
d
x
d
s
s
˙
d
y
d
t
=
d
y
d
s
s
˙
d
z
d
t
=
d
z
d
s
s
˙
(2)
\begin{cases} \frac{dx}{dt}= \frac{dx}{ds} \frac{ds}{dt}= \frac{dx}{ds}\dot{s}\\ \frac{dy}{dt}=\frac{dy}{ds}\dot{s} \\ \frac{dz}{dt}=\frac{dz}{ds}\dot{s} \\ \tag 2 \end{cases}
??????dtdx?=dsdx?dtds?=dsdx?s˙dtdy?=dsdy?s˙dtdz?=dsdz?s˙?(2)
??线速度:
v
=
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
+
(
d
z
d
t
)
2
=
s
˙
(
d
x
d
s
)
2
+
(
d
y
d
s
)
2
+
(
d
z
d
s
)
2
(3)
v=\sqrt{(\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 + (\frac{dz}{dt})^2 }=\dot{s}\sqrt{(\frac{dx}{ds})^2 +(\frac{dy}{ds})^2 + (\frac{dz}{ds})^2 }\tag{3}
v=(dtdx?)2+(dtdy?)2+(dtdz?)2?=s˙(dsdx?)2+(dsdy?)2+(dsdz?)2?(3)
??参数化路径标量的速度:
s
˙
=
v
∣
∣
N
∣
∣
(4)
\dot{s}=\frac{v}{||N||}\tag{4}
s˙=∣∣N∣∣v?(4)
??其中,
N
=
[
d
x
d
s
?
,
d
y
d
s
?
,
d
z
d
s
]
T
N=[\frac{dx}{ds}\ ,\frac{dy}{ds}\ ,\frac{dz}{ds}]^T
N=[dsdx??,dsdy??,dsdz?]T。
??式(3)对时间求一阶导数,得到:
a
=
s
¨
(
d
x
d
s
)
2
+
(
d
y
d
s
)
2
+
(
d
z
d
s
)
2
+
s
˙
2
d
x
d
s
d
2
x
d
s
2
s
˙
+
2
d
y
d
s
d
2
y
d
s
2
s
˙
+
2
d
z
d
s
d
2
z
d
s
2
s
˙
2
(
d
x
d
s
)
2
+
(
d
y
d
s
)
2
+
(
d
z
d
s
)
2
=
s
¨
?
∣
∣
N
∣
∣
+
(
s
˙
)
2
N
?
M
∣
∣
N
∣
∣
(5)
a=\ddot{s}\sqrt{(\frac{dx}{ds})^2 +(\frac{dy}{ds})^2 + (\frac{dz}{ds})^2 } + \dot{s}\frac{2\frac{dx}{ds}\frac{d^2x}{ds^2} \dot{s} + 2\frac{dy}{ds}\frac{d^2y}{ds^2} \dot{s} + 2\frac{dz}{ds}\frac{d^2z}{ds^2} \dot{s}}{2\sqrt{(\frac{dx}{ds})^2 +(\frac{dy}{ds})^2 + (\frac{dz}{ds})^2 }} \\ =\ddot{s} \ ||N|| + (\dot{s})^2\frac{N\cdot M }{||N||} \tag{5}
a=s¨(dsdx?)2+(dsdy?)2+(dsdz?)2?+s˙2(dsdx?)2+(dsdy?)2+(dsdz?)2?2dsdx?ds2d2x?s˙+2dsdy?ds2d2y?s˙+2dsdz?ds2d2z?s˙?=s¨?∣∣N∣∣+(s˙)2∣∣N∣∣N?M?(5)
??其中,
M
=
[
d
2
x
d
s
2
?
,
d
2
y
d
s
2
?
,
d
2
z
d
s
2
]
T
M=[\frac{d^2x}{ds^2}\ ,\frac{d^2y}{ds^2}\ ,\frac{d^2z}{ds^2}]^T
M=[ds2d2x??,ds2d2y??,ds2d2z?]T。
??参数化路径标量的加速度:
s
¨
=
a
?
(
s
˙
)
2
N
?
M
∣
∣
N
∣
∣
∣
∣
N
∣
∣
(6)
\ddot{s}=\frac{a-(\dot{s})^2\frac{N\cdot M }{||N||}}{||N||}\tag{6}
s¨=∣∣N∣∣a?(s˙)2∣∣N∣∣N?M??(6)
三、matlab代码
clc
clear
close all
T = 2;
n = 100;
t = linspace(0, T, n)';
s = 3 * (t / T).^2 - 2 * (t / T).^3; %归一化三次多项式
ds = (6 * (t / T) - 6 * (t / T).^2) / T;
dds = (6 - 12 * (t / T)) / T^2;
P0 = [0, 0, 0];
P1 = [10, 20, 10];
P2 = [20, 10, 50];
P3 = [40, 30, 0];
p = zeros(n, 3);
dp = zeros(n, 3);
ddp = zeros(n, 3);
for i = 1 : n
p(i, :) = (3*P1 - P0 - 3*P2 + P3)*s(i)^3 + (3*P0 - 6*P1 + 3*P2)*s(i)^2 + (3*P1 - 3*P0)*s(i) + P0; %三次贝塞尔曲线
dp(i, :) = 3 * (3*P1 - P0 - 3*P2 + P3)*s(i)^2 + 2*(3*P0 - 6*P1 + 3*P2)*s(i) + (3*P1 - 3*P0);
ddp(i, :) = 6 * (3*P1 - P0 - 3*P2 + P3)*s(i) + 2*(3*P0 - 6*P1 + 3*P2);
end
dx_s = dp(:, 1);
dy_s = dp(:, 2);
dz_s = dp(:, 3);
ddx_s = ddp(:, 1);
ddy_s = ddp(:, 2);
ddz_s = ddp(:, 3);
dx_t = dx_s .* ds;
dy_t = dy_s .* ds;
dz_t = dz_s .* ds;
ddx_t = ddx_s .* ds.^2 + dx_s .* dds;
ddy_t = ddy_s .* ds.^2 + dy_s .* dds;
ddz_t = ddz_s .* ds.^2 + dz_s .* dds;
v = sqrt(dx_t.^2 + dy_t.^2 + dz_t.^2);
a = zeros(n, 1);
for i = 1 : n
a(i) = dot([ddx_t(i), ddy_t(i), ddz_t(i)], [dx_s(i), dy_s(i), dz_s(i)]) / sqrt(dx_s(i)^2 + dy_s(i)^2 + dz_s(i)^2); %加速度往切矢量方向投影,得到切向加速度
end
ds2 = v ./ sqrt(dx_s.^2 + dy_s.^2 + dz_s.^2);
dds2 = zeros(n, 1);
for i = 1 : n
N = [dx_s(i), dy_s(i), dz_s(i)];
M = [ddx_s(i), ddy_s(i), ddz_s(i)];
dds2(i) = (a(i) - ds2(i)^2 * dot(N, M) / norm(N, 2)) / norm(N, 2);
end
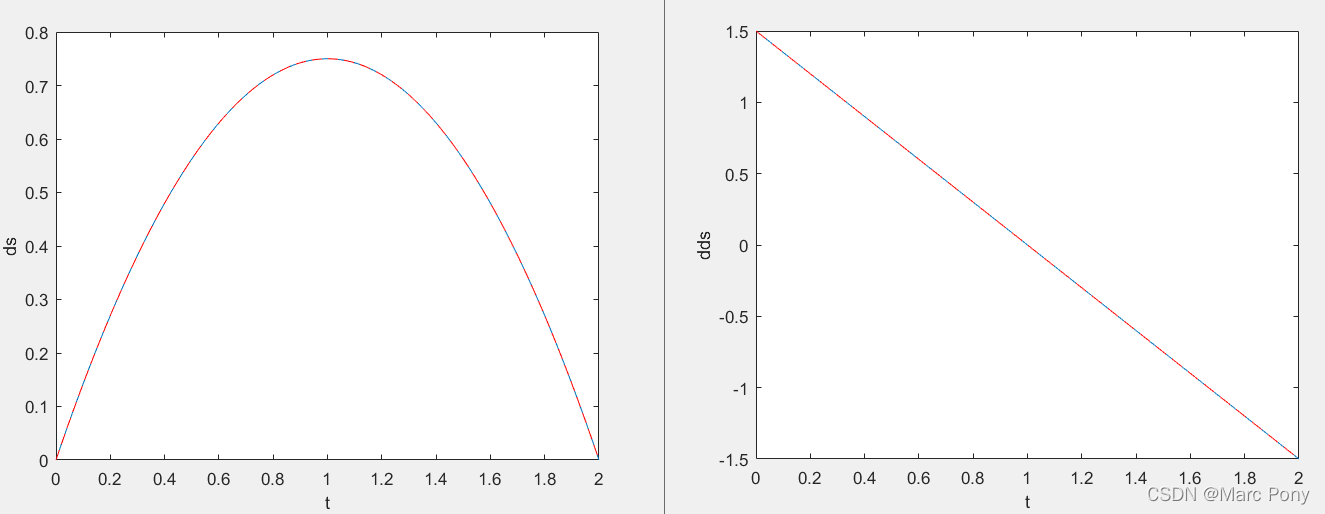
figure
plot(t, ds)
hold on
plot(t, ds2, '--r')
xlabel('t')
ylabel('ds')
figure
plot(t, dds)
hold on
plot(t, dds2, '--r')
xlabel('t')
ylabel('dds')