题目描述
Life is a game.
The world can be regarded as an undirected connected graph of nnn cities and mmm undirected roads between the cities. Now you, the life game player, are going to play the life game on the world graph.
Initially, you are at the x-th city and of k social ability points. You can earn social ability points by living and working. Specifically, you can earn ai? social ability points by living and working in the i-th city. But in this problem, you cannot earn social ability points duplicatedly in one city, so you want to travel the world and earn more social ability points. However, the roads are not easy. Specifically, there is an ability threshold wi? for the i-th road, you should be of at least wi? social ability points to go through the road. Moreover, Your social ability point will not decrease when passing roads but just need to be at least wi? if you want to go through the i-th road.
So as you can see, the life game is just living, working and traveling repeatedly. There are q game saves. For each game save, the initial city and social ability point is given and the player has not lived or worked in any city. Now you, the real life game player, need to determine the maximum possible number of social ability points you can have in the end of the game and output it for each given game save.
输入描述:
The first line contains three integers n,m,q(1≤n,m,q≤10^5), denoting the number of cities, roads and game saves respectively. The second line contains n integers a1?,a2?,?,an?(1≤ai?≤10^4), denoting the bonus social ability points for the cities. Following m lines each contains three integers u,v,w(1≤u<v≤n,1≤w≤10^9), denoting that cities u,v are undirectedly connected by a road of ability threshold w. Following q lines each contains two integers x,k(1≤x≤n,1≤k≤10^9), denoting the game saves.
输出描述:
For each game save, output one line containing one integer, denoting the maximum possible number of social ability points you can have.
输入
8 10 2 3 1 4 1 5 9 2 6 1 2 7 1 3 11 2 3 13 3 4 1 3 6 31415926 4 5 27182818 5 6 1 5 7 23333 5 8 55555 7 8 37 1 7 8 30
输出
16 36
说明
Following is a illustration of the given graph.
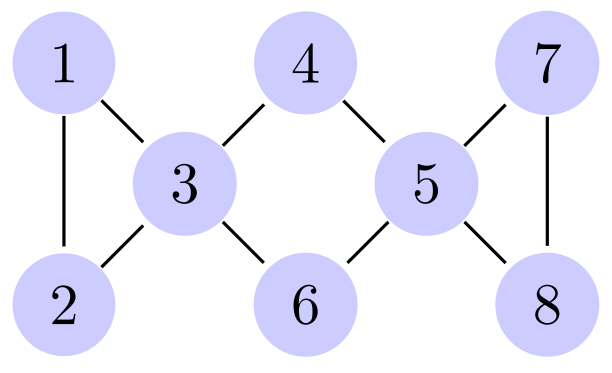
· For the first game save, you can reach 4 cities {1,2,3,4} and have 7+3+1+4+1=16 social ability points in the end
· For the second game save, you can only reach the initial city {8} and have 30+6=36 social ability points in the end
题意:?给出一棵具有n个点的树,在每个结点处都可以获得a[i]个硬币,同时每条边具有限制w[i],必须拥有不少于w[i]个硬币才可以通过这条边,共有q组询问,每次询问给出起点s和初始硬币数t,求最终能获得多少硬币。
分析:?这是一道kruskal重构树的题目,如果之前不了解这个算法可以根本无法入手。所以先简单介绍一下kruskal重构树算法,这个算法十分简单,其实就是在最小生成树的基础上增加了n-1个点,每条边对应一个点,在用kruskal构造最小生成树枚举边时,若该边可以加入最小生成树那就新增一个点,点权为边权,从该点到两集合代表元素连边,并使该点作为两集合代表元素,直至新增n-1个点。
kruskal重构树还有一些性质,比如:
1. 重构树是一个大根堆 or 小根堆
2. 原图结点都是重构树中的叶子节点
3. 原生成树两点之间的树链最大值 or?最小值是重构树上两点lca的权值
接下来考虑这道题目,先建出kruskal重构树,如下图:

编号1~8是原图结点,编号9~15是新增结点,红色数字代表新增点的点权,黄色数字代表该点能获得的硬币数。对于某个起点其实就是不断向上遍历其父节点,如果当前硬币数不小于其父节点点权,那么就可以向父节点走,同时获得父节点子树中所有的硬币,直到走到不能走的位置停下,手中的硬币数就是最终能获得的最多的硬币。
为什么是这样做呢?根据kruskal的过程,当枚举到一条可以把两连通块连接起来的边时,这条边就是能联通两区域最小的边。于是在跑kruskal时,当两连通块其中一个只有一点且为起点时,这条边就是起点到达另一个连通块的最小边,也是kruskal重构树中起点的父节点,若此时硬币数不小于该边权,那么就可以从起点走到另一个连通块,否则就会一直困在起点,当走到另一个连通块时由重构树的第一条性质可以直接获得新连通块内部所有的硬币。同样,再次遍历到一条连接包含起点的连通块的边时又得到一条最小边,也就是起点所在连通块的父节点,如果此时硬币数不少于该边权那就可以在新连通块内随意移动。转换到重构树上其实就是不断找父节点的过程。
不过由于存在极端数据,比如原图是一条边权递增的长链,此时每次询问复杂度就成了O(n)了,总的复杂度变成了O(n^2),于是要考虑优化。利用树上倍增来优化是比较好想到的,只不过具体实现时由于不同的点其限制和子树中全部硬币数都是在变化的,很难倍增到一个固定的分界点,这里很巧妙的操作就是将限制值和子树中硬币数作差,这样处理完后就一个差值在不断变化了,可以通过维护区间max值来倍增到一个分界点,在该点之上的点其差值大于初始硬币数,因此没法再往上走,优化过后的单次询问复杂度就变为了O(logn),总的复杂度为O(nlogn),轻松跑完所有数据。
具体代码如下:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <string>
#include <vector>
#define int long long
#define ll long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int n, m, fa[200005], q, cnt, num[200005], f[200005][20], _max[200005][20];
ll c[200005];
struct edge
{
int u, v, w;
}e[200005];
vector<int> to[200005];
bool cmp(edge a, edge b)
{
return a.w < b.w;
}
void dfs(int now, int fa)
{
f[now][0] = fa;
if(now != cnt)
_max[now][0] = num[fa]-c[now];
else
_max[now][0] = inf;
for(int i = 1; i < 20; i++)
{
f[now][i] = f[f[now][i-1]][i-1];
_max[now][i] = max(_max[now][i-1], _max[f[now][i-1]][i-1]);
}
for(int i = 0; i < to[now].size(); i++)
dfs(to[now][i], now);
}
int find(int x)
{
if(x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
signed main()
{
cin >> n >> m >> q;
cnt = n;
for(int i = 1; i <= n; i++)
scanf("%lld", &c[i]);
for(int i = 1; i <= 2*n-1; i++)
fa[i] = i;
for(int i = 1; i <= m; i++)
{
int u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
e[i].u = u, e[i].v = v, e[i].w = w;
}
sort(e+1, e+m+1, cmp);
int temp = 0;
for(int i = 1; i <= m; i++)
{
int u = e[i].u, v = e[i].v, w = e[i].w;
if(find(u) != find(v))
{
int U = find(u), V = find(v);
++cnt;
to[cnt].push_back(U);
to[cnt].push_back(V);
c[cnt] = c[U]+c[V];
fa[U] = cnt;
fa[V] = cnt;
num[cnt] = w;
temp++;
}
if(temp == n-1)
break;
}
dfs(cnt, 0);
for(int i = 1; i <= q; i++)
{
int now, t;
scanf("%lld%lld", &now, &t);
for(int i = 19; i >= 0; i--)
if(_max[now][i] <= t)
now = f[now][i];
printf("%lld\n", c[now]+t);
}
return 0;
}