[数据结构与算法]【ACwing】三、 动态规划：背包问题—— 3. 完全背包问题

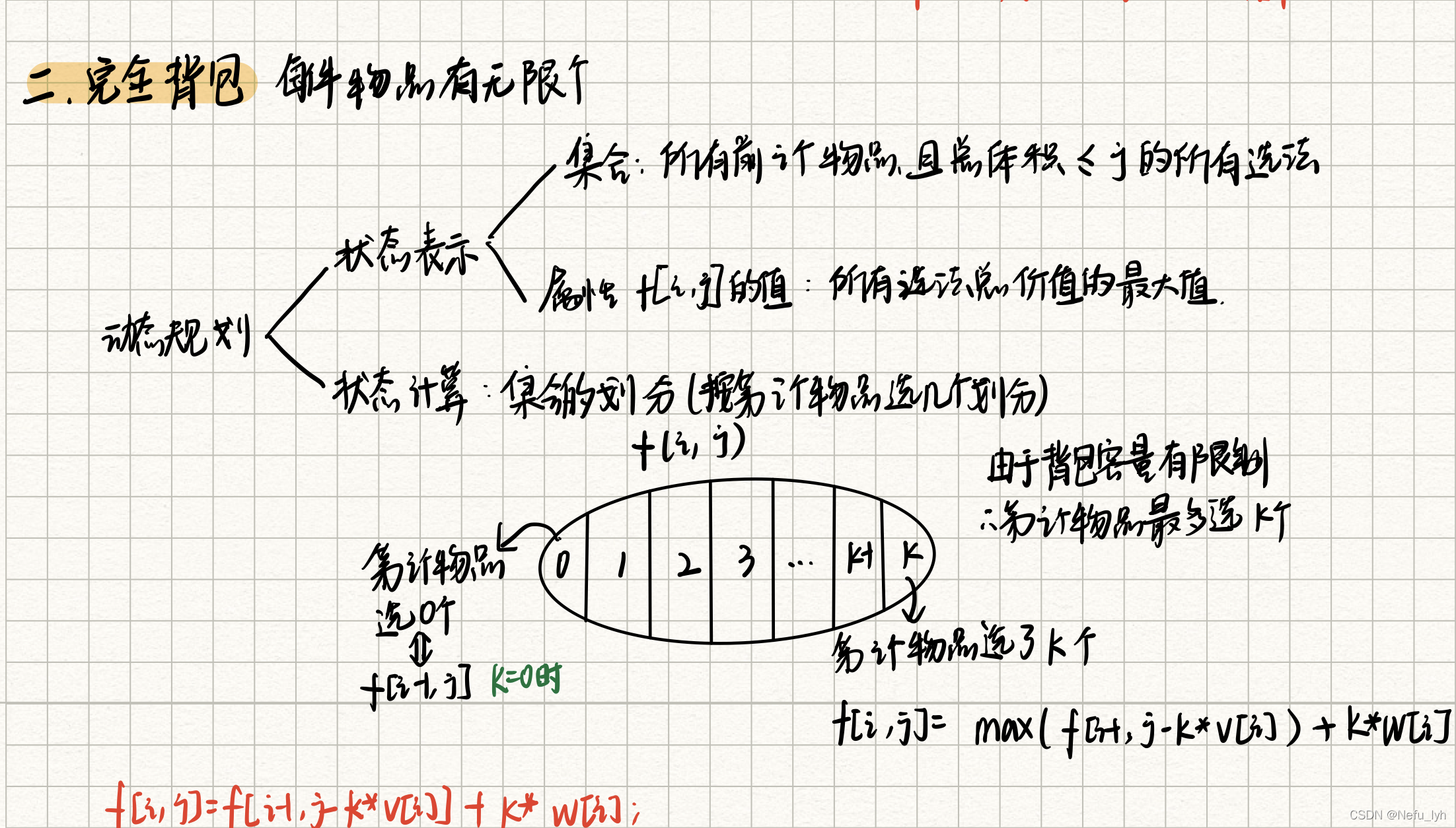
（1）知识点+模板

（2）题目

原题链接：https://www.acwing.com/problem/content/3/

（3）初级代码思路：

按照物品 i 选择几个来对集合进行划分，先循环遍历物品，再循环遍历背包数量，再遍历物品的个数（控制体积和<=容积m），那么最大价值的更新策略 = 刨去当前选择的 k 个物品 i 的最大价值 + k个物品i的价值 = f[i][j] = max(f[i][j], f[i][j - k *v[i] ] + k * w[i]);

（4）初级代码

# include <iostream>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1; i <= n; i++) cin>>v[i]>>w[i];
    for(int i = 1; i <= n; i++)//遍历所有的物品
        for(int j = 0; j <= m; j++)//每个物品在不同背包容量下
            for(int k=0; k*v[i] <= m; k++)//所选取的物品i的数量
                f[i][j] = max(f[i][j], f[i][j - k *v[i] ] + k * w[i]);
    cout<<f[n][m]<<endl;
    return 0;
}

（5）化简式子优化代码

# include <iostream>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1; i <= n; i++) cin>>v[i]>>w[i];
    for(int i = 1; i <= n; i++)//遍历所有的物品
        for(int j = 0; j <= m; j++)//每个物品在不同背包容量下
        {
            f[i][j] = f[i-1][j];//不取物品i时
            if(j>=v[i])
                 f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    cout<<f[n][m]<<endl;
    return 0;
}

（6）滚动数组优化代码

# include <iostream>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1; i <= n; i++) cin>>v[i]>>w[i];
    for(int i = 1; i <= n; i++)//遍历所有的物品
        for(int j = v[i]; j <= m; j++)//每个物品在不同背包容量下
        {
             f[j] = max(f[j],f[j-v[i]]+w[i]);
        }
    cout<<f[m]<<endl;
    return 0;
}

复盘易出错的位置

滚动数组优化后由于更新方程中需要的是 f[ i ][ j-v[i] ]，所以使用的是本层的 f[ j ]，循环正着写才对

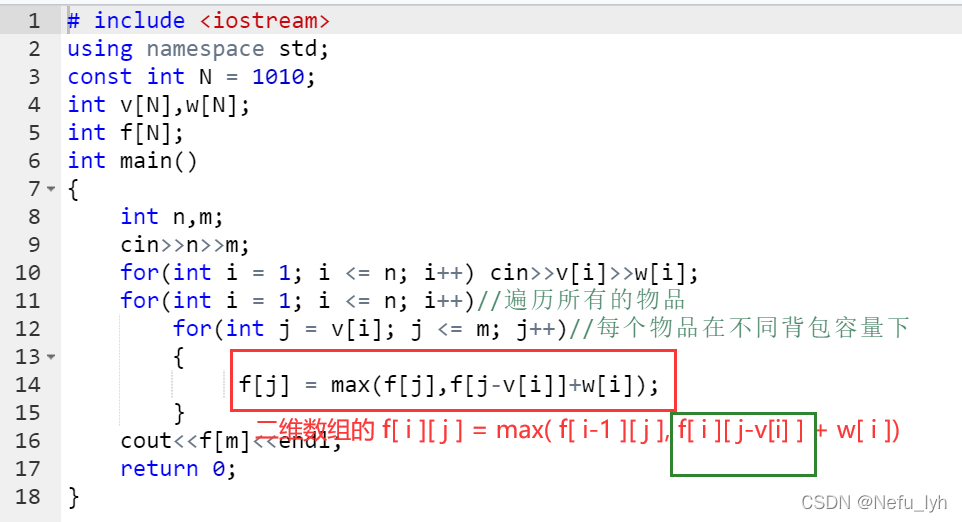
化简式子优化VS滚动数组优化的时间比较