[数据结构与算法]排序经典算法手撕代码

尊敬的读者您好：笔者很高兴自己的文章能被阅读，但原创与编辑均不易，所以转载请必须注明本文出处并附上本文地址超链接以及博主博客地址：https://blog.csdn.net/vensmallzeng。若觉得本文对您有益处还请帮忙点个赞鼓励一下，笔者在此感谢每一位读者，如需联系笔者，请记下邮箱：zengzenghe@gmail.com，谢谢合作！

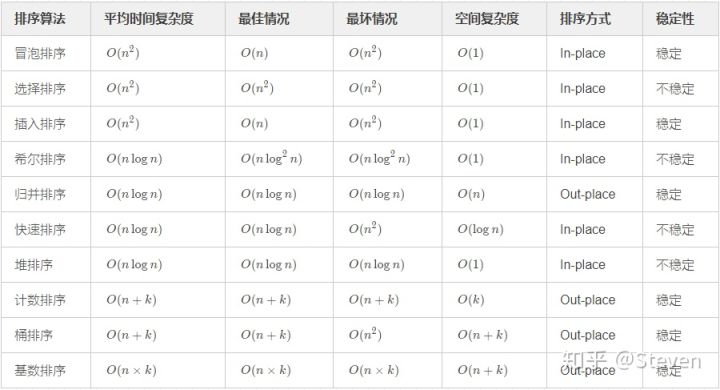
常用算法的时间复杂度比较如下：

冒泡排序(从小到大排序、稳定)?

void bubble_sort(T arr[], int n){
    //两两比较，将最大的冒泡后置
    //n个数只需要n-1趟即可排好序（最后两个元素只比较一次）
	for(int i = 0; i < n-1; i++){
	  //每一趟，最后面要保留排好序的数且j+1不能越界，所以限制j<n-i-1
	  for(int j = 0; j < n-1-i; j++){
	     if(arr[j] > arr[j+1]){
	     	swap(arr[j], arr[j+1]);
	     }
	  }
	}	
}

选择排序(从小到大排序、不稳定)

void select_sort(T arr[], int n){
    //从剩余序列中找出最小值下标，并交换至前面
    //剩余数值中只有两个元素时，只需要比较一次，所以i < n-1
	for(int i = 0; i < n-1; i++){
	    //min用于记录最小值索引，首先是剩余序列第一个值做最小参考
		int min = i;
		//通过比较找出剩余序列中的最小值索引
		for(int j = i+1; j < n; j++){
			if(arr[j]<arr[min])
				min = j;
		}
		//将最小值前置
		swap(arr[i], arr[min]);
	}
}

插入排序(从小到大排序，稳定，插入排序的一种改进版本希尔排序不稳定)

void insert_sort(T arr[], int n){
	//遍历需要向前插入的元素
	for(int i = 1; i < n; i++){
	    //保存当前待插入的元素，以免覆盖后无法使用
	    int val = arr[i];
	    //先定义j，以免内层循环break掉后，j因释放掉而无法使用
	    int j;
	    //将待当前待插入元素与前面有序序列进行比较
		for(j = i - 1; j >= 0; j--){
		    //如果比待插入元素大则将元素进行向后赋值移动(赋值覆盖)，否则val值应该插入j+1的位置
		 	if(val<arr[j]){
		 		arr[j+1]=arr[j];
		 	}
		 	else
		 	break;
		}
		将val值应该插入j+1的位置
		arr[j+1] = val;
	}
}

归并排序(从小到大排序 稳定)

void(T arr[], int l, int mid int r){
	//先建立辅助空间保存需要合并的数值
	T aux[r-l+1];
	for(int i=l; i<=r; i++){
       //aux从0开始，arr从开始
	   aux[i-l] = arr[i];
	}
    //基于aux辅助数据进行比较合并，同时赋值给arr
    int i = l;
    int j = mid+1;
	for(int k=l; k<=r; k++){
	    //左侧没数可比，用右侧数据直接填补
		if(i > mid){
			arr[k] = aux[j-l];
			j++;
		}
		//右侧没数可比，用左侧数据直接填补
		else if(j < r){
			arr[k] = aux[i-l];
			i++;
		}
		//当右侧小，则将右侧赋值arr
		else if (aux[i-l]>aux[j-l]){
		    arr[k] = aux[j-l];	
		    j++;
		//当左侧小，则将左侧赋值arr
		else {
			arr[k] = aux[i-l];
			i++;
		}
	  }
	}
}


void merge_sort_recursive( T arr[], int l, int r){
    int mid = l+(r-l)/2;
    //对左边继续分
	merge_sort_recursive(arr, l, mid);
	//对右边继续分
	merge_sort_recursive(arr, mid+1, r);
	//如果左边的末尾值小于等于右边的首值，则无需合并
	if(arr[mid] > arr[mid+1])
	   merge(arr, l, mid, r);

}


void merge_sort(T arr[], int n){
	merge_sort_recursive(arr, 0, n-1)
}

快速排序(从小到大排序、不稳定)

int partition(int arr[], int l ,int r){
	int p_value = arr[l];
	int i = l+1;
	int j = r;
	while(true){
		while(i<=r && arr[i] < p) i++;
		while(j>=l+1 && arr[i] > p) j--;
		if(i>j) break;
		//等于p的情况 也可以交换
		swap(arr[i],arr[j]);
		i++;
		j--;
	}
	swap(arr[j], arr[l]);
    return j;
}


void quick_sort_recursive(int arr[], int l, int r){
    //获取标定点
	int p = partition(arr, l, r);
	//p已经找到了合适的位置，故无需参与后续排序
	//对左侧进行快排
	quick_sort_recursive(arr, l, p-1);
	//对右侧进行快排
	quick_sort_recursive(arr, p+1, r);
}

void quick_sort(T arr[], int n){
	quick_sort_recursive(arr, 0, n-1);
}

堆排序(从小到大排序、不稳定)

#无处安放的e
woid shut_down_1(int arr[]; int n; int k){
    //保存待执行shutdown非叶子节点的值
    int e = arr[k];
    while(2*k+1 < n){
    	int j = 2*k+1;
    	//如果左值小于右值，则将最大索引记为右侧值，否则默认将最大索引记为左侧值
    	if(j+1<n && arr[j]<arr[j+1]){
    		j=j+1;
    	}
    	//如果保存值大于左右值，则非叶子节点找到了合适的位置，否则需要继续寻找
    	if(e >= arr[j]) break;
    	//直接用子节点值赋值叶子节点，会使得arr[k]与arr[j]的值是一样的，所以最终还需更新arr[k]的值
    	arr[k] = arr[j];
    	//改变k值，此时arr[k]不是用于执行shutdown非叶子节点的值，所以比较时还是用的e 
    	k = j;
    }
    //比较时用的e, 最终还需赋值给arr[k], 以实现放置合适的位置
    arr[k] = e;
}

#有处安放的e
woid shut_down_2(int arr[]; int n; int k){
    while(2*k+1 < n){
    	int j = 2*k+1;
    	//如果左值小于右值，则将最大索引记为右侧值，否则默认将最大索引记为左侧值
    	if(j+1<n && arr[j]<arr[j+1]){
    		j=j+1;
    	}
    	//如果保存值大于左右值，则非叶子节点找到了合适的位置，否则需要继续寻找
    	if(arr[k] >= arr[j]) break;
    	//直接交换子节点值与叶子节点值，会使得arr[k]与arr[j]的值是不一样的，所以最终无需更新arr[k]的值
    	swap(arr[k], arr[j]);
    	//改变k值，此时arr[k]仍是用于执行shutdown非叶子节点的值
    	k = j;
    }
}


void heap_sort(T arr[], int n){
    //从最后一个非叶子节点(n-1)/2开始建立最大堆, 直到所有非叶子节点均已shutdown
	for(int i=(n-1)/2; i>=0; i--)}{
    	shut_down(arr, n, i);
	}
	//最后一个元素无需交换，所以i>0
	for(int i=n-1; i>0; i--){
	   //将最大堆的第一个数与最后一个数交换位置
	   swap(arr[0],arr[i]);
	   //去掉最后一个元素，再次建立最大堆
	   shut_down(arr, i, 0);
	}
}

日积月累，与君共进，增增小结，未完待续。