题目链接
题意:
首先给你三个数n,m,q,表示的是图上有n个节点, m条边,q个询问,每个点都有权重,每条边都有一个边权,这个边权表示要想从这条边上的一个点走到另一个点手中的权值必须比这条边的权重,每经过一个点都会获得这个点的权重,每次询问给你两个数x,y,让你求从x点出发,初始权值是y,最多能获得多少权重。
分析:
这个题考的是kruskal重构树,什么是kruskal重构树呢,下面有张图片
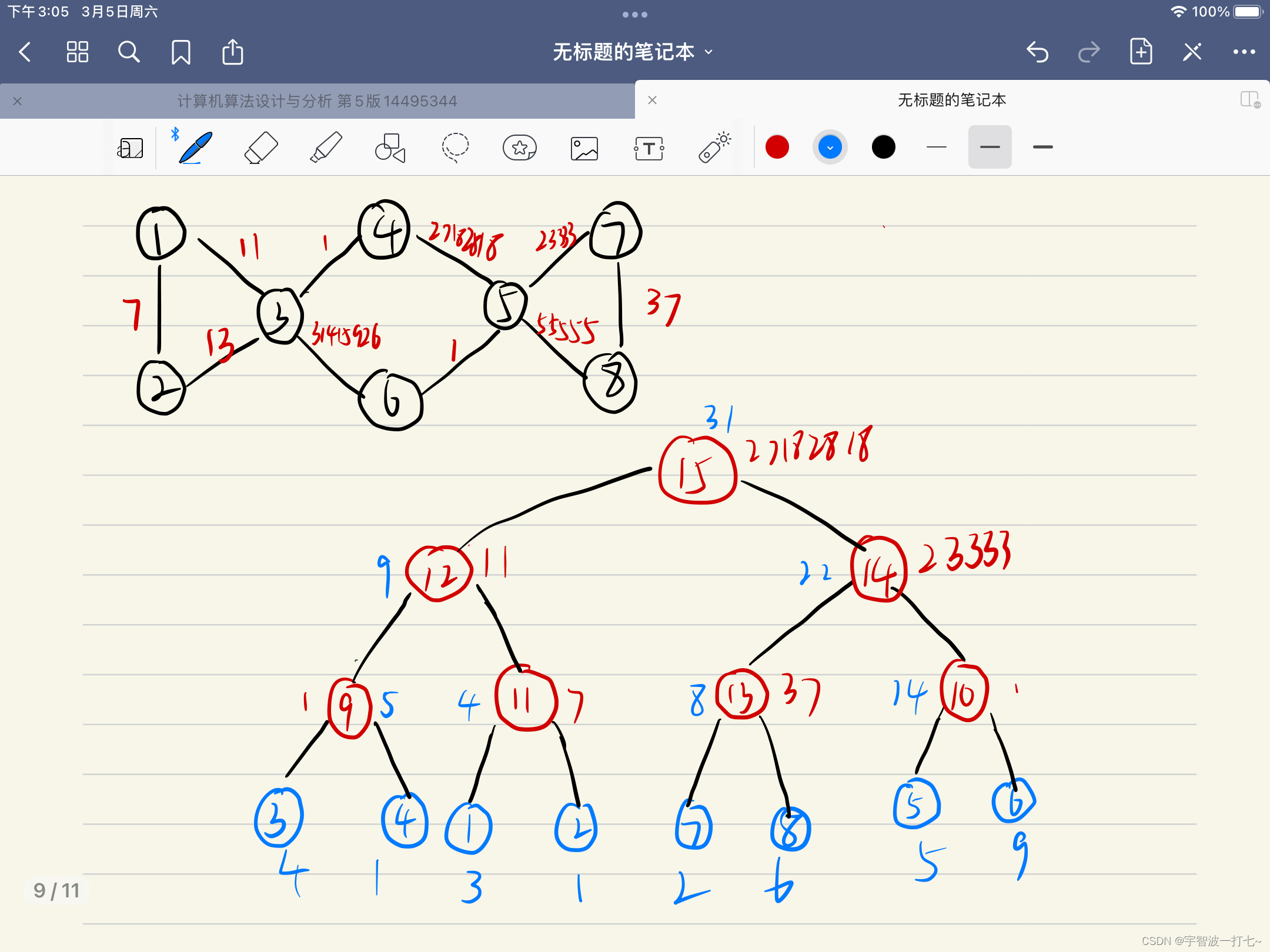
上面那张图是题目中建立的图,那么下面那个树就是kruskal重构树啦,那么是怎么重构的呢?那么我来解释一下,因名而义,kruskal重构树是在用kruskal算法建立最小生成树的过程中来建立起来的,它的所有叶子节点都是原图中的节点,它的所有非叶子节点全都是后来加上的节点,加节点的规则就是当并查集的集合合并的时候加一个点作为两个集合根节点的父节点,这个新加的点的权值就是两集合之间的边的边权,那么这么做以后会形成一棵树,而且是大根堆!!!!就叫他kruskal重构树,那么这棵树的性质就是很符合当前的题目了,当现在拥有的权重比这个节点的权重大的话,这个人就能访问这个以这个节点为根节点的子树中的所有叶节点,所以说现在咱们能想到的方法就是记录一个节点的父节点,相当于没有路径压缩的并查集,那么只要是当前的权重比它的父亲节点的权值大,那么就能走上去,如此循环往复则能得到答案,但是有一种情况是不能忽视的,就是一条长链,那么一定会超时,所以说这个写法也T在了第50%的样例上,下面请看朴素版的kruskal重构树写法吧
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>
#include<cstdlib>
#include<climits>
#include<unordered_map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
typedef unsigned long long ull;
const int mod = 1e9+7;
const int N = 200010,M = N*2;
int n,m,T,idx,h[N],e[M],ne[M],w[M],a[N],pa[N],t,cnt[N],v[N];
struct node{
int x,y,w;
bool operator<(const node&t)const{
return w < t.w;
}
}ed[N];
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int find(int x){
if(x != pa[x]) pa[x] = find(pa[x]);
return pa[x];
}
int main(){
scanf("%d%d%d",&n,&m,&T);
t = n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]),w[i] = a[i];
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
ed[i].x = a,ed[i].y = b,ed[i].w = c;
}
sort(ed+1,ed+1+m);
for(int i=1;i<=2*n;i++) pa[i] = i;
for(int i=1;i<=m;i++){
int px = find(ed[i].x),py = find(ed[i].y);
if(px != py){
v[++t] = ed[i].w;
pa[px] = t;
pa[py] = t;
w[t] = w[px] + w[py];
add(px,t);add(py,t);
}
}
while(T--){
int st,tt;
scanf("%d%d",&st,&tt);
LL ans = 0,t = tt;
while(h[st] != -1 && v[st] <= tt){
ans = w[st] + t;
tt = w[st] + t;
st = e[h[st]];
}
if(v[st] <= tt) ans = w[st] + t;
printf("%lld\n",ans);
}
return 0;
}
那么现在咱们应该想一下怎么优化了,优化的话首先想一下哪一些地方是可有可无的,当最后的答案是最上面的节点,那么咱们从最下面一直走上去是不是有点慢,咱们是不是一下子直接跳上去比较好,那么我牛逼的队友就提出来了树上倍增,树上倍增具体是个什么东西呢,也可以说成是二进制优化吧,我们用fa[u][i]表示u节点上面第2^i层父节点是谁,首先要明白具体含义,其次就是求这个数组了,其实也挺好理解的,采用的是递推的思想,就是 i = i/2 + i/2,fa[u][i] = fa[ fa[u][i-1] ][i-1],就是能从u的第2^(i-1)层父节点再加上2的(i-1)次方推过来,那么咱们这样最多只需要跳logn次就能找到最终的答案了,不过还得进行一下预处理就是处理一下第i层节点的权值与以i-1层节点为根节点的子树中的总权重的差值,咱们现在只需要判断输入的初始值与这个差值之间的关系就行了,下面具体请看代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>
#include<cstdlib>
#include<climits>
#include<unordered_map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
typedef unsigned long long ull;
const int mod = 1e9+7;
const int N = 200010,M = N*2;
int n,m,T,idx,h[N],e[M],ne[M],sum[M],a[N],pa[N],t,cnt[N],v[N],fa[N][20],mi[N][20];
struct node{
int x,y,w;
bool operator<(const node&t)const{
return w < t.w;
}
}ed[N];
int find(int x){
if(x != pa[x]) pa[x] = find(pa[x]);
return pa[x];
}
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs1(int u,int f){
sum[u] = a[u];fa[u][0] = f;
for(int i=1;i<=18;i++) fa[u][i] = fa[fa[u][i-1]][i-1];
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
if(j == f) continue;
dfs1(j,u);
sum[u] += sum[j];
}
}
void dfs2(int u,int f){
mi[u][0] = v[f] - sum[u];
for(int i=1;i<=18;i++) mi[u][i] = max(mi[u][i-1],mi[fa[u][i-1]][i-1]);
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
if(j == f) continue;
dfs2(j,u);
}
}
int main(){
scanf("%d%d%d",&n,&m,&T);
t = n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
ed[i].x = a,ed[i].y = b,ed[i].w = c;
}
sort(ed+1,ed+1+m);
for(int i=1;i<=2*n;i++) pa[i] = i;
for(int i=1;i<=m;i++){
int px = find(ed[i].x),py = find(ed[i].y);
if(px != py){
v[++t] = ed[i].w;
pa[px] = t;
pa[py] = t;
add(t,px);add(t,py);
}
}
dfs1(n*2-1,0);
dfs2(n*2-1,0);
while(T--){
int st,tt;
scanf("%d%d",&st,&tt);
for(int i=18;i>=0;i--) if(tt>=mi[st][i]&&fa[st][i]) st = fa[st][i];
printf("%lld\n",sum[st]+tt);
}
return 0;
}
/*
8 10 2
3 1 4 1 5 9 2 6
1 2 7
1 3 11
2 3 13
3 4 1
3 6 31415926
4 5 27182818
5 6 1
5 7 23333
5 8 55555
7 8 37
1 7
8 30
*/