开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 数据库规范化理论大题考点 -> 正文阅读

[数据结构与算法]数据库规范化理论大题考点

数据库规范化理论大题考点

文章目录

数据库规范化理论大题考点

1.Closure of Attributes 属性集的闭包相关题型

1.1 属性集闭包的算法

result:= α;
	repeat
		for each 函数依赖β→r in F do
			begin
				if β 蕴涵于 result then result := result ∪ r;
			end
       	until (result 不变)

对函数依赖集F下的每一个函数依赖，如果依赖的左边 $\beta$ 在结果属性集中，那么依赖的右边 $\gamma$ 加入到结果集中。重复直至result不变

例1：计算属性闭包

$Example :Given\ R<U,F>, R = {A,B,C,D},F={B\rightarrow CD,AD\rightarrow E,B\rightarrow A}\$

$BC)^+?$

解：
$1.Result = \{BC\}\\ 2.Result = \{ABCD\}\\ 3.Result = \{ABCDE\}$

例2：判断函数依赖是否成立

定理： $X\rightarrow Y\Leftrightarrow Y\subseteq (X_F)^+$

$AB)_F^+ = \{A,B,C,D,E\}$ ， $AB\rightarrow E$ 成立

1.2 最小依赖的计算

算法：

函数依赖的右部分解成单属性的函数依赖
去掉函数依赖的左部的冗余属性
去掉冗余的函数依赖

例子

例1
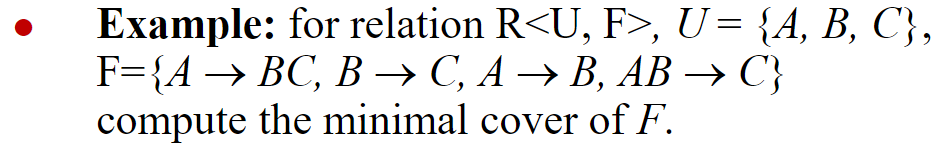
- 分解
$\{A\rightarrow B,A\rightarrow C,B\rightarrow C,AB\rightarrow C\}$
- 去掉左部冗余属性
  
  考察 $AB\rightarrow C$ 中B是否冗余。即考虑函数依赖集F是否逻辑蕴含函数依赖集 $F_1 = \{A\rightarrow B,A\rightarrow C,B\rightarrow C,A\rightarrow C\}$
  
  计算 $A_F^+ = \{BC\}\supe {C}$ ，所以B冗余，去除
  
  得到 $F_1 = \{A\rightarrow B,A\rightarrow C,B\rightarrow C\}$
- 去除冗余的函数依赖
  
  计算属性闭包 $A^+_{F_1-(A\rightarrow C)} = {ABC}\supe {C}$ ，所以函数依赖 $A\rightarrow C$ 多余，得到 $F_2 = \{A\rightarrow B,B\rightarrow C\}$

1.3 正则覆盖的计算

正则覆盖可以由最小覆盖合并得到。

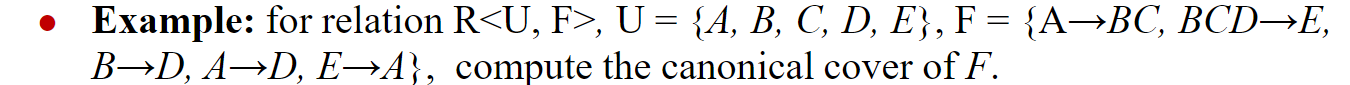
step1：分解右部
$\{A\rightarrow B,A\rightarrow C,BCD\rightarrow E,B\rightarrow D,A\rightarrow D,E\rightarrow A\}$
step2：去除左部的冗余属性

考察 $BCD\rightarrow E$ 中B是否冗余，即考察函数依赖集F是否逻辑蕴含函数依赖集 $F_1 = \{A\rightarrow B,A\rightarrow C,CD\rightarrow E,B\rightarrow D,A\rightarrow D,E\rightarrow A\}$ ，计算 ${ } (CD)_F^+ = \{\}$ ，所以B不冗余。
考察 $BCD\rightarrow E$ 中C是否冗余，即考察函数依赖集F是否逻辑蕴含函数依赖集 $F_2 = \{A\rightarrow B,A\rightarrow C,BD\rightarrow E,B\rightarrow D,A\rightarrow D,E\rightarrow A\}$ ，计算 ${ } (BD)_F^+ = \{\}$ ，所以C不冗余。
考察 $BCD\rightarrow E$ 中D是否冗余，即考察函数依赖集F是否逻辑蕴含函数依赖集 $F_3 = \{A\rightarrow B,A\rightarrow C,BC\rightarrow E,B\rightarrow D,A\rightarrow D,E\rightarrow A\}$ ，计算 $(BC)_F^+ = \{ABCDE\}\supe {E}$ ，所以D冗余。

去除冗余属性得 $F_3 = \{A\rightarrow B,A\rightarrow C,BC\rightarrow E,B\rightarrow D,A\rightarrow D,E\rightarrow A\}$

step3：去除多余的函数依赖

对于函数依赖 $A\rightarrow D$ ，计算 $(A)^+_{F_3-(A\rightarrow D)} = \{ABCDE\}\supe {D}$ ，所以函数依赖多余，去除得 $F_4 = \{A\rightarrow B,A\rightarrow C,BC\rightarrow E,B\rightarrow D,E\rightarrow A\}$

step4：合并

$F_{canoncal} = \{A\rightarrow BC,BC\rightarrow E,B\rightarrow D,E\rightarrow A\}$

2. 候选码的计算

算法：

例题

例1：

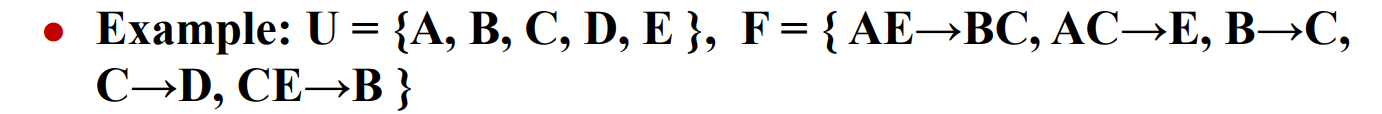
step1：X = {A}

step2： $A_F^+ = A$ ，所以单独的A不是候选码

step3： $AB)_F^+ = U$ ，所以AB是候选码

? $AC)_F^+ = U$ ，所以AC是候选码

? $AE)_F^+=U$ ，所以AE是候选码

? Y为空集

结束，所有的候选码为AB,AC,AE

2.1 候选码计算的应用

2.1.1 2NF的判断

2NF要求不存在非主属性对码的部分依赖，所以需要找出所有的候选码，确认非主属性，和是否有其对码的部分依赖的情况。

Example：R(A, B,C,D), F = {AB → C, AC → BD}

step1：求出所有的候选码

候选码集合为{AB, AC}

step2：非主属性，得到非主属性为D

step3：构造完整依赖： $AB\rightarrow D$ 和 $AC\rightarrow D$ ，判断这两个函数依赖中有无冗余属性。若无则不存在部分依赖，否则存在。

计算 $A)_F^+ = ?$ ， $B)_F^+ = ?$ ， $C)_F^+ = ?$ ，即无冗余属性，所以不存在部分依赖，满足2NF

2.1.2 3NF的判断

3NF的计算也是需要计算出所有的候选码的。进而判断 $\beta-\alpha$ 的属性是不是在候选码中。

Example：R(A, B, C, D), F = {AB → C, C → D}，判断是否属于第三范式。

step1：候选码计算

$AB)_F^+ = U$ ，所以AB即是候选码。

step2：对于函数依赖 $C\rightarrow D$ ，对应 $C：\alpha，D：\beta$ ，那么 $\beta-\alpha = D$ 不属于候选码

所以该范式非第三范式

3.Decomposition

3.1 无损分解和依赖保持的判定

Examples: R = ( A, B, C ) F = { A → B, B → C }

Decomposition1: R1 = (A, B), R2 = (B, C)

? IS Lossless-join ?
$R_1\cap R_2 = B\\ B\rightarrow R_2成立，所以该分解为Lossless-Join\ Decomposition$
? IS Dependency preserving?
$F_1 = \{A\rightarrow B\}\\ F_2 = \{B\rightarrow C\}\\ (F_1\cup F_2)^+=F^+,所以该分解是依赖保持的$

Decomposition2: R1 = (A, B), R2 = (A, C)

? IS Lossless-join ?
$R_1\cap R_2 = A\\ A\rightarrow R_1成立，所以该分解为Lossless-Join\ Decomposition$
? IS Dependency preserving?
$F_1 = \{A\rightarrow B\}\\ F_2 = \{A\rightarrow C\}\\ (F_1\cup F_2)^+≠F^+,所以该分解不是依赖保持的$

3.2 BCNF的无损分解

Examples:

emp_info ( emp_id, emp_name, epm_phone, dept_name, dept_phone, dept_mgrname, skill_id, skill_name, skill_date, skill_lvl )

Fc = { emp_id → (emp_name, epm_phone, dept_name ), dept_name → ( dept_phone, dept_mgrname) , skill_id → skill_name, (emp_id, skill_id , skill_date )→ skill_lvl }

CK: (emp_id, skill_id , skill_date )

要求：Decomposition to BCNF

step1：emp_id不是码，将emp_id决定的最大的关系模式取出，得到：

R1 = {emp_id, emp_name, epm_phone, dept_name, dept_phone, dept_mgrname}

有函数依赖：

F1 : {emp_id → emp_name, epm_phone, dept_name; dept_name → dept_phone, dept_mgrname}，

在原关系模式中去除右半部分，得到：

R2 = {emp_id, skill_id, skill_name, skill_date, skill_lvl}

有函数依赖：

F2 = {skill_id → skill_name, (emp_id, skill_id , skill_date)→ skill_lvl}

step 2 ：在R1中仍有dept_name不是超码，继续分解R1

R11 = {dept_name, dept_phone, dept_mgrname}