前言

保持二叉搜索树对展开的敏感性，对前缀和后缀(或前驱后继)的敏感性，对dummy的敏感性。
保持敏感性才能达到问题直接转化和问题的传递性转化。
如:
-> 二叉搜索树与其展开形式相关
-> 展开形式和链表相关
-> 链表又和dummy相关(统一操作除了dummy，回溯时叶子节点的特殊合并也可以统一操作)
-> 有序的链表又和双指针相关，如果转化成有序的数组又和二分相关
-> 从而关联起了二叉搜索树和双指针。

一、案例

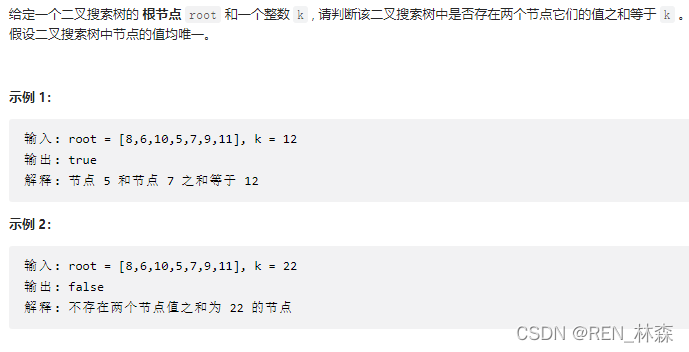
在这里插入图片描述

二、题解

1、Set的应用

1）Set的应用，记录 K - root.val 是否存在，来快速解题。

public boolean findTarget(TreeNode root, int k) {
        //set快速解题
        Set<Integer> cache = new HashSet<>();
        order(root, k, cache);
        return res;
    }

    boolean flag = false;//用于剪枝
    boolean res = false;

    private void order(TreeNode root, int k, Set<Integer> cache) {
        if (flag || root == null) return;

        int m = k - root.val;
        if (cache.contains(m) && !flag) {
            flag = true;
            res = true;
        }
        cache.add(root.val);
        order(root.left, k, cache);
        order(root.right, k, cache);
    }

2、S-O(h)优化

1）展开二叉搜索树 + dummy统一操作 + 双指针寻找和为K。

//空间O(h)，将二叉搜索树展开成双向链表。 + dummy节点来统一空树操作。+双指针寻找是否有和为k的两个值。
    TreeNode dummyHead = new TreeNode(-1), dummyTail = new TreeNode(-1);

    public boolean findTarget2(TreeNode root, int k) {
        dummyHead.right = dummyTail;
        dummyTail.left = dummyHead;

        inOrder(root);
        dummyHead = dummyHead.right;
        dummyTail = dummyTail.left;
        while (dummyHead != dummyTail) {
            int gap = k - dummyHead.val - dummyTail.val;

            if (gap == 0) return true;

            if (gap > 0) {
                dummyHead = dummyHead.right;
                continue;
            }
            dummyTail = dummyTail.left;
        }
        return false;
    }

    private void inOrder(TreeNode root) {
        if (root == null) return;

        inOrder(root.left);
        TreeNode right = root.right;

        dummyTail.left.right = root;
        root.left = dummyTail.left;
        root.right = dummyTail;
        dummyTail.left = root;

        inOrder(right);
    }

    // Definition for a binary tree node.
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }