[数据结构与算法]CodeForces - 1646E Power Board （思维，数学）

题目链接：点击这里

题目大意：
给定一个 $n\times m$ 的矩阵，其中 $a[i][j]=i^j$ ，求这个 $n\times m$ 的矩阵有多少个不同的元素
一个 $3\times 3$ 的矩阵如下图所示：

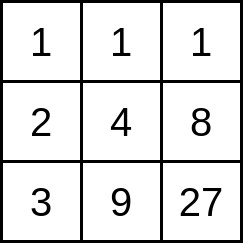
题目分析：
不难想到，如果两行有相同的元素，那么两行的形式必然是 $a^b$ 和 $a^c$
例如第 $2,4,8$ 行其元素分别为：
$2^1,2^2,...,2^m$
$2^2,2^4,...,2^{2?m}$
$2^3,2^6,...,2^{3?m}$
我们如何求这三行的不同元素个数呢
我们发现，如果两个数相同，那么指数必然相同，所以我们可以把指数用一个矩阵表达出来：
$1,2,...,m$
$2,4,...,2?m$
$3,6,...,3?m$
问题就转化成了求这个矩阵中有多少个不同元素，由于是指数，所以该矩阵最大行号也就是 $\log n$ ，我们可以用暴力直接算出前 $i$ 行有多少个不同元素，然后存在一个数组 $cnt[i]$ 里
对于答案，我们直接对这 $n$ 行进行一个遍历，如果当前数没被标记，就把当前数的倍数全部标记，同时记录最大指数 $a$ 是多少，然后把答案加 $cnt[a]$ 即可

具体细节见代码：

// Problem: E. Power Board
// Contest: Codeforces - Codeforces Round #774 (Div. 2)
// URL: https://codeforces.com/contest/1646/problem/E
// Memory Limit: 256 MB
// Time Limit: 1500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

//#pragma GCC optimize(2)
//#pragma GCC optimize("Ofast","inline","-ffast-math")
//#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<queue>
#include<unordered_map>
#define ll long long
#define inf 0x3f3f3f3f
#define Inf 0x3f3f3f3f3f3f3f3f
//#define int  ll
#define endl '\n'
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
using namespace std;
int read()
{
	int res = 0,flag = 1;
	char ch = getchar();
	while(ch<'0' || ch>'9')
	{
		if(ch == '-') flag = -1;
		ch = getchar();
	}
	while(ch>='0' && ch<='9')
	{
		res = (res<<3)+(res<<1)+(ch^48);//res*10+ch-'0';
		ch = getchar();
	}
	return res*flag;
}
const int maxn = 1e6+5;
const int mod = 1e9+7;
const double pi = acos(-1);
const double eps = 1e-8;
int n,m,cnt[25];
bool vis[maxn],vis2[maxn*20];
void init(int m)
{
	int sum = 0;
	for(int i = 1;i <= 20;i++)
		for(int j = 1;j <= m;j++)
		{
			if(!vis2[i*j])
			{
				vis2[i*j] = true;
				sum++;
			}
			cnt[i] = sum;
		}
}
int main()
{
	n = read(),m = read();
	init(m);
	ll res = 1;
	for(int i = 2;i <= n;i++)
	{
		if(!vis[i])
		{
			ll cur = i,a = 1;
			while(cur <= n)
			{
				vis[cur] = true;
				cur *= i;
				a++;
			}
			a--;
			res += cnt[a];
		}
	}
	cout<<res<<endl;
	return 0;
}