[数据结构与算法]团队程序设计天梯赛-3.3排位赛总结

7-1 心理阴影面积 (5 分)

题目

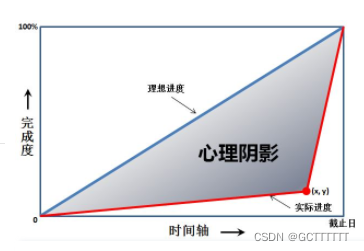
这是一幅心理阴影面积图。我们都以为自己可以匀速前进（图中蓝色直线），而拖延症晚期的我们往往执行的是最后时刻的疯狂赶工（图中的红色折线）。由红、蓝线围出的面积，就是我们在做作业时的心理阴影面积。

现给出红色拐点的坐标 (x,y)，要求你算出这个心理阴影面积。

输入格式：
输入在一行中给出 2 个不超过 100 的正整数 x 和 y，并且保证有 x>y。这里假设横、纵坐标的最大值（即截止日和最终完成度）都是 100。

输出格式：
在一行中输出心理阴影面积。

友情提醒：三角形的面积 = 底边长 x 高 / 2；矩形面积 = 底边长 x 高。嫑想得太复杂，这是一道 5 分考减法的题……

输入样例：

90 10

输出样例：

4000

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
	
	int x, y;
	cin >> x >> y;
	cout << 5000 - 50 * y - (100 - x) * 50;
	return 0;
}

7-2 世÷我＝佬 (5 分)

题目

本题目要求读入2个正整数A和B，然后输出A是否可以整除B。

输入格式:
两个正整数A和B（保证在整形范围内）。

输出格式:
A可以整除B则输出YES，否则输出NO。

输入样例1:

5 5

输出样例1:

YES

输入样例2:

2 3

输出样例2:

NO

注意点

原理很简单，就取模0，然后判断一下分母为0的情况，但因为x和y的顺序，我本来写的是x%y0但差一个点（A可以整除B不是x%y吗？？？？），但反过来写y%x就满分 过了…

代码

#include <bits/stdc++.h>
using namespace std;
int main(){
	long long x,y;
	cin>>x>>y;
	if(x==0) cout<<"NO";
	else if(y%x==0) cout<<"YES";
	else cout<<"NO";
//	if(x%y==0) cout<<"YES";
	else if(y==0) cout<<"NO";
//	else cout<<"NO";
}

7-3 求集合数据的均方差 (10 分)

题目

设计函数求 N 个给定整数的均方差。若将 N 个数 A[ ] 的平均值记为 Avg，则均方差计算公式为：

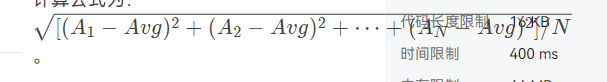
输入格式：
输入首先在第一行给出一个正整数 N（≤10
4
），随后一行给出 N 个正整数。所有数字都不超过 1000，同行数字以空格分隔。

输出格式：
输出这N个数的均方差，要求固定精度输出小数点后5位。

输入样例 1：

10
6 3 7 1 4 8 2 9 11 5

输出样例 1：

3.03974

输入样例 2：

1
2

输出样例 2：

0.00000

知识点

pow(x,y):求x的y次方
sqrt（a）：求a的开方

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	int n;
	cin >> n;
	int a[10000];
	int sum = 0;
	for(int i=0; i<n; i++) {
		cin >> a[i];
		sum += a[i];
	}
	double avg = 1.0*sum/n;
	double res;
	for(int i=0; i<n; i++) res += pow(a[i]-avg, 2);
	printf("%.5f", sqrt(res/n));
	return 0;
}

7-4 程序运行时间 (10 分)

题目

题目来自PAT (Basic Level) Practice： 要获得一个 C 语言程序的运行时间，常用的方法是调用头文件 time.h，其中提供了 clock() 函数，可以捕捉从程序开始运行到 clock() 被调用时所耗费的时间。这个时间单位是 clock tick，即“时钟打点”。同时还有一个常数 CLK_TCK，给出了机器时钟每秒所走的时钟打点数。于是为了获得一个函数 f 的运行时间，我们只要在调用 f 之前先调用 clock()，获得一个时钟打点数 C1；在 f 执行完成后再调用 clock()，获得另一个时钟打点数 C2；两次获得的时钟打点数之差 (C2-C1) 就是 f 运行所消耗的时钟打点数，再除以常数 CLK_TCK，就得到了以秒为单位的运行时间。

这里不妨简单假设常数 CLK_TCK 为 100。现给定被测函数前后两次获得的时钟打点数，请你给出被测函数运行的时间。

输入格式:
输入在一行中顺序给出 2 个整数 C1 和 C2。注意两次获得的时钟打点数肯定不相同，即 C1 < C2，并且取值在 [0,10
7
]。

输出格式:
在一行中输出被测函数运行的时间。运行时间必须按照 hh:mm:ss（即2位的 时:分:秒）格式输出；不足 1 秒的时间四舍五入到秒。

输入样例:

123 4577973

输出样例:

12:42:59

知识点

四舍五入函数：round（）
格式化输出

代码

#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
int main() {
	int x, y;
	cin >> x >> y;
	int z = round((y-x)/100.0);
	int h = z/3600;
	int m = z%3600/60;
	int s = z%3600%60;
	printf("%02d:%02d:%02d", h, m, s);
}

7-5 判断题 (15 分)

题目

判断题的评判很简单，本题就要求你写个简单的程序帮助老师判题并统计学生们判断题的得分。

输入格式：
输入在第一行给出两个不超过 100 的正整数 N 和 M，分别是学生人数和判断题数量。第二行给出 M 个不超过 5 的正整数，是每道题的满分值。第三行给出每道题对应的正确答案，0 代表“非”，1 代表“是”。随后 N 行，每行给出一个学生的解答。数字间均以空格分隔。

输出格式：
按照输入的顺序输出每个学生的得分，每个分数占一行。

输入样例：

3 6
2 1 3 3 4 5
0 0 1 0 1 1
0 1 1 0 0 1
1 0 1 0 1 0
1 1 0 0 1 1

输出样例：

13
11
12

思路

设置学生答案、正确答案、分数数组对应进行 记录就可

代码

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main() {
	int n, m;
	cin >> n >> m;
	int s[100];
	int ans[100];
	int x;
	for(int i=0; i<m; i++) cin >> s[i];
	for(int i=0; i<m; i++) cin >> ans[i];
	for(int i=0; i<n; i++) {
		int sum = 0;
		for(int j=0; j<m; j++) {
			cin >> x;
			if(x==ans[j]) sum += s[j];
		}
		cout << sum << endl;
	}
	return 0;
}

7-6 黑洞数 (15 分)

题目

黑洞数也称为陷阱数，又称“Kaprekar问题”，是一类具有奇特转换特性的数。

任何一个各位数字不全相同的三位数，经有限次“重排求差”操作，总会得到495。最后所得的495即为三位黑洞数。所谓“重排求差”操作即组成该数的数字重排后的最大数减去重排后的最小数。（6174为四位黑洞数。）

例如，对三位数207：

第1次重排求差得：720 - 27 ＝ 693；
第2次重排求差得：963 - 369 ＝ 594；
第3次重排求差得：954 - 459 ＝ 495；
以后会停留在495这一黑洞数。如果三位数的3个数字全相同，一次转换后即为0。

任意输入一个三位数，编程给出重排求差的过程。

输入格式：
输入在一行中给出一个三位数。

输出格式：
按照以下格式输出重排求差的过程：

序号: 数字重排后的最大数 - 重排后的最小数 = 差值
序号从1开始，直到495出现在等号右边为止。

输入样例：

123

输出样例：

1: 321 - 123 = 198
2: 981 - 189 = 792
3: 972 - 279 = 693
4: 963 - 369 = 594
5: 954 - 459 = 495

思路

求每个数重排后的最大最小值：排序后按从小到大的数字排得到的就是最小值，按从大到小的顺序排就是最大值，我当时用的是3位数的数组（每个数字一位），然后排序，用a[0]*100+a[1]*10+a[2]来算出每次的数，参考代码中是将每个数转换为字符串后进行排序，然后再转回int来进行运算

知识点

• to_string():将数字转为对应的字符串型
• stoi():将字符串转为int整型
• 字符串与数值的相互转换
  关于字符串与数值间的转换：C++11的字符串与数值间的类型转换：to_string() stoi stol stoul stoll stof stod stold

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	string a, b;
	cin >> a;
	b = a;
	int i = 0;
	while(++i) {
		sort(a.begin(), a.end());
		sort(b.begin(), b.end(), greater<char>());
		int res = stoi(b)-stoi(a);
		printf("%d: %d - %d = %d\n", i, stoi(b), stoi(a), res);
		if(res==495) break;
		a = b = to_string(res);
	}
}

7-7 说反话-加强版 (20 分)

题目

给定一句英语，要求你编写程序，将句中所有单词的顺序颠倒输出。

输入格式：
测试输入包含一个测试用例，在一行内给出总长度不超过500 000的字符串。字符串由若干单词和若干空格组成，其中单词是由英文字母（大小写有区分）组成的字符串，单词之间用若干个空格分开。

输出格式：
每个测试用例的输出占一行，输出倒序后的句子，并且保证单词间只有1个空格。

输入样例：

Hello World   Here I Come

输出样例：

Come I Here World Hello

思路

利用cin对空格的处理特点来分隔单词
运用栈进行倒序输出
注意：在windows控制台运行，回车后按[CTRL]+[Z]结束输入

代码

#include<iostream>
#include<stack>
#include<string>
using namespace std;
int main() {
	stack<string> s;
	string str;
	
	while(cin>>str)//如果在windows控制台运行，回车后按[CTRL]+[Z]结束输入
		s.push(str);
	int flag = 0;
	while(!s.empty()) {
		if(flag) cout << " ";
		cout << s.top();
		s.pop();
		flag = 1;
	}
	return 0;
}

7-8 刮刮彩票 (20 分)

题目

“刮刮彩票”是一款网络游戏里面的一个小游戏。如图所示：
每次游戏玩家会拿到一张彩票，上面会有 9 个数字，分别为数字 1 到数字 9，数字各不重复，并以 3×3 的“九宫格”形式排布在彩票上。

在游戏开始时能看见一个位置上的数字，其他位置上的数字均不可见。你可以选择三个位置的数字刮开，这样玩家就能看见四个位置上的数字了。最后玩家再从 3 横、3 竖、2 斜共 8 个方向中挑选一个方向，方向上三个数字的和可根据下列表格进行兑奖，获得对应数额的金币。

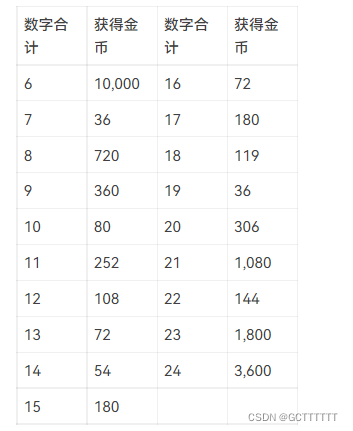
现在请你写出一个模拟程序，模拟玩家的游戏过程。

输入格式:
输入第一部分给出一张合法的彩票，即用 3 行 3 列给出 0 至 9 的数字。0 表示的是这个位置上的数字初始时就能看见了，而不是彩票上的数字为 0。

第二部给出玩家刮开的三个位置，分为三行，每行按格式 x y 给出玩家刮开的位置的行号和列号（题目中定义左上角的位置为第 1 行、第 1 列。）。数据保证玩家不会重复刮开已刮开的数字。

最后一部分给出玩家选择的方向，即一个整数： 1 至 3 表示选择横向的第一行、第二行、第三行，4 至 6 表示纵向的第一列、第二列、第三列，7、8分别表示左上到右下的主对角线和右上到左下的副对角线。

输出格式:
对于每一个刮开的操作，在一行中输出玩家能看到的数字。最后对于选择的方向，在一行中输出玩家获得的金币数量。

输入样例:

1 2 3
4 5 6
7 8 0
1 1
2 2
2 3
7

输出样例:

1
5
6
180

思路

• 使用数组存放对应点数的奖金
• 模拟输入点数（这里要注意题目说的是1-9中的数字，顺序可以打乱，我原本以为都是1-9顺序的，看了图才反应过来，注意要看清楚题意）
• 补全那个原本就知道的数字（我当时是用一个1-9的数组，输入过就设为true，剩下那个false的就是那个数，参考代码用的是求和sum最后用45-sum得到那个数）
• 然后选择开奖的方向（注意不用判断该方向上是否都看得到，而是此方向上的所有都要刮开并计算）

代码

#include<iostream>
using namespace std;
int main() {
	int score[] = {
		0,0,0,0,0,0,10000,36,720,360,80,252,108,72,54,180,72,180,119,36,306,1080,144,18
		00,3600
	};
	int a[4][4];
	int i, j, x, y;
	int vx, vy;
	int sum = 0;
	for(i=1; i<=3; i++)
		for(j=1; j<=3; j++) {
			cin >> x;
			sum += x;
			if(x==0) vx = i, vy = j;
			else a[i][j] = x;
		}
	a[vx][vy] = 45 - sum;
	for(i=0; i<3; i++) {
		cin >> x >> y;
		cout << a[x][y] << endl;
	}
	cin >> x;
	if(x<=3)//行
		sum = a[x][1] + a[x][2] + a[x][3];
	else if(x<=6)//列
		sum = a[1][x-3] + a[2][x-3] + a[3][x-3];
	else if(x==7)//左斜线
		sum = a[1][1] + a[2][2] + a[3][3];
	else //右斜线
		sum = a[1][3] + a[2][2] + a[3][1];
	cout << score[sum];
}

7-11 是否完全二叉搜索树 (25 分)

题目

将一系列给定数字顺序插入一个初始为空的二叉搜索树（定义为左子树键值大，右子树键值小），你需要判断最后的树是否一棵完全二叉树，并且给出其层序遍历的结果。

输入格式：
输入第一行给出一个不超过20的正整数N；第二行给出N个互不相同的正整数，其间以空格分隔。

输出格式：
将输入的N个正整数顺序插入一个初始为空的二叉搜索树。在第一行中输出结果树的层序遍历结果，数字间以1个空格分隔，行的首尾不得有多余空格。第二行输出YES，如果该树是完全二叉树；否则输出NO。

输入样例1：

9
38 45 42 24 58 30 67 12 51

输出样例1：

38 45 24 58 42 30 12 67 51
YES

输入样例2：

8
38 24 12 45 58 67 42 51

输出样例2：

38 45 24 58 42 12 67 51
NO

思路

• 利用二叉树结点编号的特点，使用int数组即可。
• 要判断是否完全，看最大编号是否为n就行
• 注意是比根节点大的放左边，比根节点小的放右边

知识点

用int数组存二叉树结点编号！！！
最大编号为n证明前面全部满了，即为完全二叉树

关键点

插入的函数：（模拟输入每个数时插入二叉树的情况并用int数组存起来）

void insert(int x) {
	int id = 1;
	while(a[id]!=0) { //找插入位置
		if(x>a[id]) id = id*2;//左孩子下标
		else id = id*2+1;//右孩子下标
	}
	a[id] = x;
	mmax = max(id, mmax);
}

看看每一步数组的情况：
用例1：

9
38 45 42 24 58 30 67 12 51

最后1~n都是有数字的，证明是完全的二叉树
用例2：

8
38 24 12 45 58 67 42 51

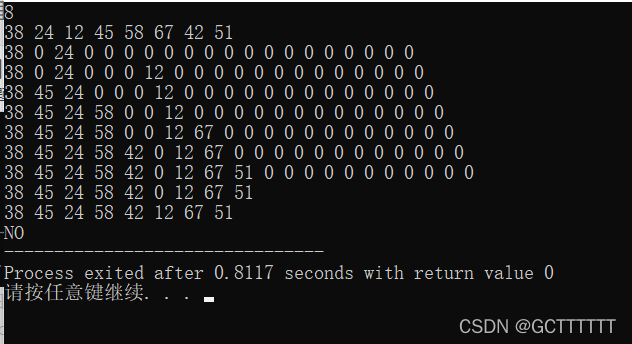
可以看到数组中有0，即该地方没有插入数字，最后的mmax>n，证明不是完全的二叉树

技巧

这有个技巧可以搞分，就是使用随机数！！如果只会输出层次的二叉树而不会判断yes还是no可以用随机数碰碰运气
注意想要随机数真正随机要加个随机数种子（用当前时间来作为种子）
代码：

srand(time(0));
if(rand()/(double)RAND_MAX>0.5) cout<<"\nYES";
else cout<<"\nNO"; 

其中rand()/(double)RAND_MAX的作用是将随机数范围限制在0-1之间
更详细的rand解说参考：C++产生随机数

代码

#include<bits/stdc++.h>
using namespace std;
int a[100];
int mmax = 1;
int root;
void insert(int x) {
	int id = 1;
	while(a[id]!=0) { //找插入位置
		if(x>a[id]) id = id*2;//左孩子下标
		else id = id*2+1;
	}
	a[id] = x;
	mmax = max(id, mmax);
}
int main() {
	int n;
	cin >> n;
	cin >> root;
	a[1] = root;
	for(int i=1; i<n; i++) {
		int x;
		cin >> x;
		insert(x);
//		for(int i=1;i<=20;i++){
//		cout<<a[i]<<" ";
//	}
//	cout<<'\n';
	}
//	for(int i=1;i<=mmax;i++){
//		cout<<a[i]<<" ";
//	}
//	cout<<'\n';
	cout << root;
	for(int i=2; i<=mmax; i++)
		if(a[i]) cout << " " << a[i];
	if(mmax==n) cout << "\nYES";
	else cout << "\nNO";
}

7-12 三足鼎立 (25 分)

题目

当三个国家中的任何两国实力之和都大于第三国的时候，这三个国家互相结盟就呈“三足鼎立”之势，这种状态是最稳定的。

现已知本国的实力值，又给出 n 个其他国家的实力值。我们需要从这 n 个国家中找 2 个结盟，以成三足鼎立。有多少种选择呢？

输入格式：
输入首先在第一行给出 2 个正整数 n（2≤n≤10
5
）和 P（≤10
9
），分别为其他国家的个数、以及本国的实力值。随后一行给出 n 个正整数，表示n 个其他国家的实力值。每个数值不超过 10
9
，数字间以空格分隔。

输出格式：
在一行中输出本国结盟选择的个数。

输入样例：

7 30
42 16 2 51 92 27 35

输出样例：

9

样例解释：
能联合的另外 2 个国家的 9 种选择分别为：

{16, 27}, {16, 35}, {16, 42}, {27, 35}, {27, 42}, {27, 51}, {35, 42}, {35, 51}, {42, 51}。

思路

• 先排序，再比较。如果使用顺序查找会超时
• 使用基于二分查找的upper_bound和lower_bound

知识点

• lower_bound(a+i+1, a+n, mmax);//返回指向第一个大于等于mmax的指针：C++ lower_bound()函数用法详解
• upper_bound(a+i+1, a+n, mmin);//返回指向第一个大于mmin的指针：C++ upper_bound()函数（精讲版）
  找到个好东西：c语言中文网的stl教程（很详细）
• 用自己的值加上当前遍历到的城市的值得到mmax，自己的值减去当前遍历到的城市的值的绝对值得到mmin，则满足条件形成三足鼎立的城市应该处于(mmin,mmax)的范围内，因此找出第一个大于等于mmax的指针l，和第一个大于mmin的指针，则l-r即为遍历到此城市时总共满足条件的城市个数（注意要先对数组进行排序才能这样做），使用cnt不断加上每次的城市数即可得到答案

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	int n, a[100000];
	int me;
	cin >> n >> me;
	for(int i=0; i<n; i++) cin >> a[i];
	sort(a, a+n);
	long long cnt = 0;
	for(int i=0; i<n; i++) {
		long long mmax = me+a[i], mmin = abs(me-a[i]);
		auto l = lower_bound(a+i+1, a+n, mmax);//返回指向第一个大于等于mmax的指针
		auto r = upper_bound(a+i+1, a+n, mmin);//返回指向第一个大于mmin的指针
		cnt += l-r;
	}
	cout << cnt;
	return 0;
}

7-10 畅通工程之最低成本建设问题 (25 分)

题目

某地区经过对城镇交通状况的调查，得到现有城镇间快速道路的统计数据，并提出“畅通工程”的目标：使整个地区任何两个城镇间都可以实现快速交通（但不一定有直接的快速道路相连，只要互相间接通过快速路可达即可）。现得到城镇道路统计表，表中列出了有可能建设成快速路的若干条道路的成本，求畅通工程需要的最低成本。

输入格式:
输入的第一行给出城镇数目N (1<N≤1000)和候选道路数目M≤3N；随后的M行，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号（从1编号到N）以及该道路改建的预算成本。

输出格式:
输出畅通工程需要的最低成本。如果输入数据不足以保证畅通，则输出“Impossible”。

输入样例1:

6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3

输出样例1:

12

输入样例2:

5 4
1 2 1
2 3 2
3 1 3
4 5 4

输出样例2:

Impossible

思路

• 本质是求最小生成树。
• 代码一中使用并查集实现prim算法
• 代码二中使用并查集实现Kruskal算法

知识点

• 求最小生成树：详解：最小生成树
• prim算法求最小生成树原理：详解：prim算法（普里姆算法）详解
• Kruskal算法求最小生成树原理：详解：kruskal算法（克鲁斯卡尔算法）详解
• 并查集实现prim算法
• 并查集实现Kruskal算法
• 两种方法求并查集集合根节点
  1、

int find(int x) {
	while(x!=root[x]) x = root[x];
	return x;
}

2、

int find(int x) {
//while(x!=fa[x]) x = fa[x];
//return x;
	return x==fa[x]? x:fa[x]=find(fa[x]);
}

代码一

#include<bits/stdc++.h>
using namespace std;
int n, m;
int root[1001];
multimap<int, pair<int, int>> mp;//允许有相同键值，仍然按键值排序
//并查集 
int find(int x) {//求根节点 
	while(x!=root[x]) x = root[x];
	return x;
}
void un(int x, int y) {
	int px = find(x);
	int py = find(y);
	root[px] = py;
}
//并查集实现prim算法求最小生成树 
int prim() {
	int cnt = n;
	int sum = 0;
	while(!mp.empty() && cnt>1) {
		auto tmp = mp.begin()->second;//获得剩下权值最小的那条边的两个顶点
		int x = find(tmp.first);//求两个顶点的集合的根
		int y = find(tmp.second);
		int len = mp.begin()->first;//这条边的长度
		mp.erase(mp.begin());
		if(x==y) continue;//在同一个连通分量
		//根节点相同则说明两点已经在一个连通的边集合中，因此跳过不用加入sum 
		un(x, y);//x与y之间有通路，因此合并 
		sum += len;
		cnt--;
	}
	if(cnt>1) return -1;//cnt>1证明通路数（mp中保存的)用完了但仍有 点未连接，即无法构成通路 
	else return sum;
}
int main() {
	cin >> n >> m;
	while(m--) {
		int a, b, c;
		cin >> a >> b >> c;
		mp.insert({c, {a, b}});//注意<int,pair<int,int>>和pair<int,int>如何新建表示 
	}
	for(int i=1; i<=n; i++) root[i] = i;
	int res = prim();
	if(res==-1) cout << "Impossible";
	else cout << res;
	return 0;
}

代码二：

#include<bits/stdc++.h>
using namespace std;
int n, m;
int fa[1001];
struct node {
	int x, y, w;
} a[3001];
bool cmp(node a, node b) {
	return a.w < b.w;
}
int find(int x) {
//while(x!=fa[x]) x = fa[x];
//return x;
	return x==fa[x]? x:fa[x]=find(fa[x]);//另一种方法求根节点！！！ 
}
int kru() {
	int cnt = n;
	int sum = 0;
	for(int i=0; i<m && cnt>1; i++) {
		int x = find(a[i].x);//求两个顶点的集合的根
		int y = find(a[i].y);
		if(x!=y) {
			fa[x] = y;
			sum += a[i].w;
			cnt--;
		}
	}
	if(cnt>1) return -1;
	else return sum;
}
int main() {
	cin >> n >> m;
	for(int i=0; i<m; i++) cin >> a[i].x >> a[i].y >> a[i].w;
	sort(a, a+m, cmp);//根据每条通路长度从小到大排 
	for(int i=1; i<=n; i++) fa[i] = i;
	int res = kru();
	if(res==-1) cout << "Impossible";
	else cout << res;
	return 0;
}

• 7-9 直捣黄龙 (25 分)
• 7-13 目录树 (30 分)