[数据结构与算法]AcWing 1118. 分成互质组

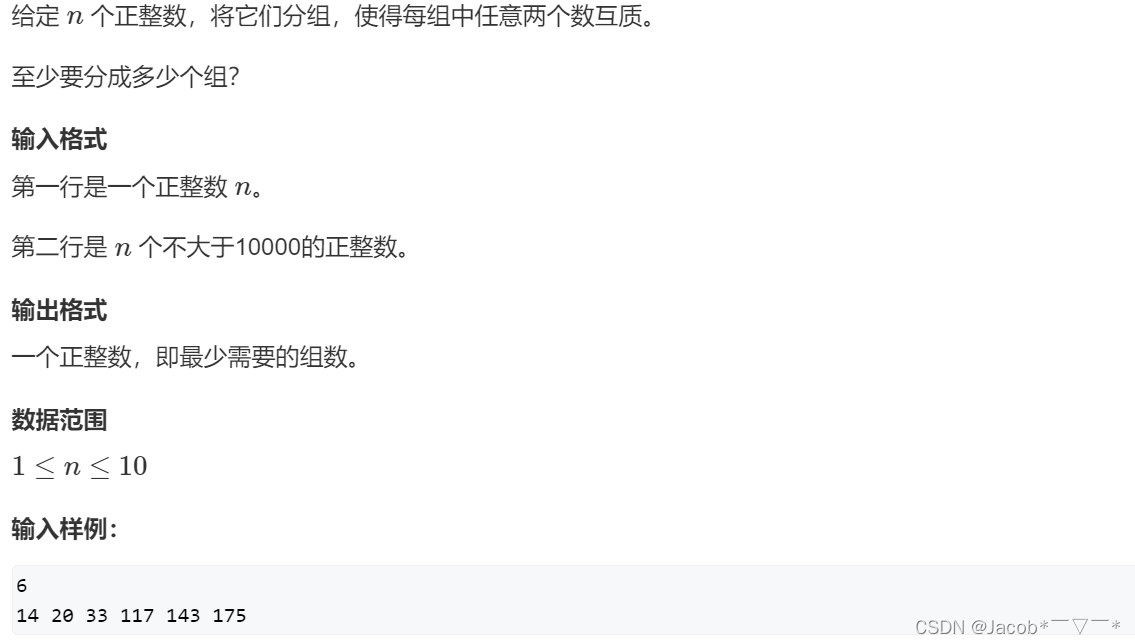
题意：

给定 n 个正整数，将它们分组，使得每组中任意两个数互质。

问：至少要分成多少个组？

思路：

dfs，对每一个元素，我们有两种操作：

• ①：放到现有组中的最后一组中（依次枚举最后一组的所有元素，判断新加的元素是否与它们全部互质，如果是的则加入）
• ②：新开一个组并放入

用p[N]存放n个元素
二维数组group[N][N]存放每个组

我们从第一个组 g=1，组内没有数 gc=0，当前用掉了 cnt=0 个元素，当前组还未开始遍历数 start=0 的初始状态开始搜索。

每次搜索的时候判断是否可以将元素放到现有组中的最后一组（用标记变量ok），如果不行再新开一组。

空白代码：

#include<bits/stdc++.h>

using namespace std;
const int N = 15;
int group[N][N], p[N];
bool st[N];
int n;
int ans;

int gcd(int a, int b)
{
    return b ? gcd(b, a%b) : a;
}

bool check(int g[], int gc, int a){
    for(int i=0;i<gc;++i)
    {
        if(gcd(g[i], a)!=1) return false;
    }
    return true;
}

void dfs(int g, int gc, int cnt, int start)
{
    if(g>=ans) return ;
    if(cnt==n) {ans = g; return ;}
    
    bool ok = false;
    for(int i=start; i<n; ++i)
    {
        if(!st[i]&&check(group[g], gc, p[i]))
        {
            st[i] = true;
            group[g][gc] = p[i];
            dfs(g, gc+1, cnt+1, i+1);
            st[i] = false;
            ok = true;
        }
    }
    if(!ok) dfs(g+1, 0, cnt, 0);
}

int main()
{
    cin>>n;
    for(int i=0;i<n;++i) cin>>p[i];
    ans = n;
    dfs(1, 0, 0, 0);
    cout<<ans<<endl;
    
    return 0;
}

代码 + 注释：

#include<bits/stdc++.h>
using namespace std;

const int N = 15;

int n;
int p[N];//存放n个元素
int group[N][N];//存放每个组
bool st[N];
int ans;

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

bool check(int g[], int gc, int a){//判断当前组中的数是否和该数都互质(即该数能否放进该组)
    for(int i=0;i<gc;++i)//枚举此组组内每个数
    {
        if(gcd(g[i], a)!=1) return false;//只要组内有数和该数不互质了就return false
    }
    return true;//否则return true
}

void dfs(int g, int gc, int cnt, int start)
{
    //g为当前的最后一组的组的序号,gc为当前组内 搜索到的 数的序号
    //cnt为当前 搜索过的 元素数量,start为当前组 开始搜索的 数(p数组中的元素)的序号

    if (g >= ans) return;//如果有比当前最优解所需的组数更多的解法说明此解不为最优解-->直接return即可
    if (cnt == n) {ans = g; return ;}//如果搜完了所有点了,说明此解为当前的最优解,更新最优解
    
    bool ok = false;//flag标记是否能新开一组
    for (int i = start; i < n; ++i)//枚举每个数
        if (!st[i] && check(group[g], gc, p[i]))//如果当前数还未被放进组里 且 与当前的组中的数都互质
        {
            st[i] = true;
            group[g][gc] = p[i];
            //分支一：继续搜索该组,组内数的数量gc + 1,总的数的数量cnt + 1,搜索的数的序号i + 1（组合型枚举，人为规定一个递增的顺序）
            dfs(g, gc + 1, cnt + 1, i + 1);
            st[i] = false;
            ok = true;//如果能放进当前最后一组,则不用新开一组,ok标记为true
        }
        
    //分支二 经过for的枚举后发现无法放进最后一组,ok没有发生什么变化,还是false,则新开一组来搜索
    if (!ok) dfs(g + 1, 0, cnt, 0);
    //当前最后一组的组的序号g + 1, 组内搜索的数的序号gc为0
    //搜索到的数cnt未变, 当前组内开始搜索的数的序号start为0(仍重新从0开始搜,放不放入新开的组内就看是否满足条件了)
}

int main()
{
    cin >> n;
    ans = n;//还未搜索时,假定最优解为最坏的情况每个数都分一组
    for (int i = 0; i < n; ++i) cin >> p[i];
    dfs(1, 0, 0, 0);
    //从第一个组 g=1, 组内没有数 gc=0
    //当前用掉了 cnt=0 个元素, 当前组还未开始遍历数 start=0 的初始状态开始搜索
    
    cout << ans << endl;
    return 0;
}