定积分的概念与基本性质
定积分的定义

这三个符号分别的意思分别是
所有区间里最宽的那个区间,第i个小区间上的任意点,第i个小区间的长度

几个注解,注意一下,第四个,那个地方是负号是因为你看函数表达式啊,+和-1

第六点是之前提到过的定积分的定义

两个小例题,巩固一下你对于定积分定义的理解
定积分的基本性质

定积分的几个基本性质,着重注意一下5和7,重点
给出积分中值定理的证明;

积分中值定理的证明

注意一下,积分中值定理是可能取到端点值的
定积分基本性质的推广

积分中值定理的推广

这个是很重要很关键的地方,和你之前一个地方连起来了,就是如果你需要用罗尔的话,那么必须保证那两个函数值相等的点的x不相等。
然后如果你用的是积分中值定理的话,那么就不能保证这一点了,但是如果你用推广的积分中值定理的话就可以了。
基本理论
下面是预备知识



两个注解
积分基本定理
定理1 引理

定理内容及其证明

几个注解


- 如果只看不定积分式子,x是常数,t才是变量
- 然后这个x你不能把它放在式子里面,由于它是常数,你可以直接给它拆分
- 洛必达,注意定积分求导之后的样子
- 你做不出来了,你需要凑出导数的样子,然后利用一下题目给出的条件你就能做出来了。
定理2 牛顿莱布尼茨公式
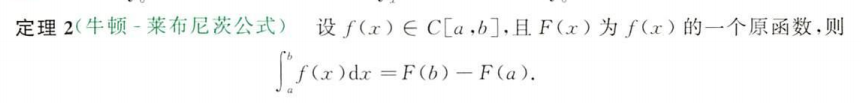

牛顿莱布尼茨的证明,利用到了定理1,引理
定积分的特殊性质
1.对称区间上函数的定积分性质
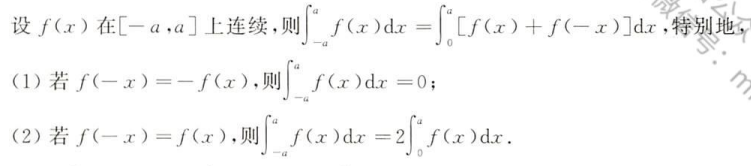

证明部分

这个对称公式确实挺有用的
2.三角函数定积分的性质
性质一
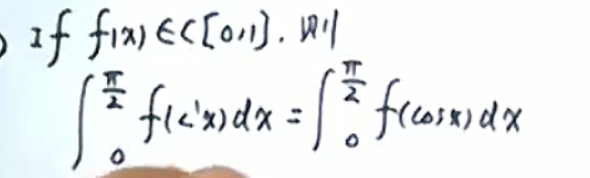

意思就是这个意思,就是x+t等于a+b(左边的)就可以了
比如下面这个例子说a+t等于-a,然后左边的下线是-a,于是右边的下限就是0了
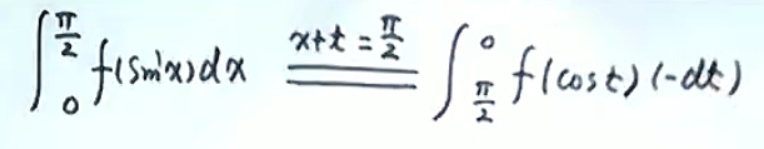

对于那个微分的变换的方式,就是两边求微分

证出来了

- 不定积分的公式你在定积分里面照样用,就是你需要注意一下积分限也需要变换
- 变换是这样变换的,相加是这样相加的,说实话,很妙
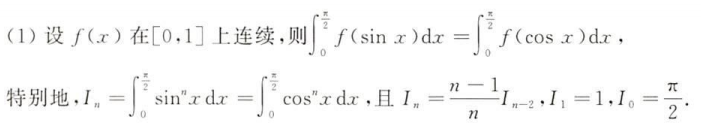
特别的性质,说实话,看了例子之后会发现很好用

看了之后发现这个很好用

要不直接一整题挖空?
(挖空位置随点)
- 看到可以变成平方和去变
- 尽量全部都变成一个形态的
- 积分的话,你里面的东西无所谓,直接替换,就是你的积分限需要变一下
- 考虑把平方和乘出来
- 发现对称区间,找机会利用以下奇函数和偶函数的规则
插播一下奇函数和偶函数的加减乘除规则
乘除就是把奇函数当作负数,偶函数当作正数,规则一样
加减:
两个奇函数或者偶函数相加减还是奇函数偶函数
一个基函数和偶函数相加减是非奇非偶函数

最后那个是I4

这种第二问你必须得找机会用到第一问的结论
在这里插入图片描述
做题就是找指引,无指引,不做题,你也做不了题,从题目给你的信息中找到蛛丝马迹,看他想要你怎么走

小积累
性质二


cos用这个公式的条件
一步一步全部都是知识点



这里最后一步的两倍是因为不是0到Π/2而是0到Π


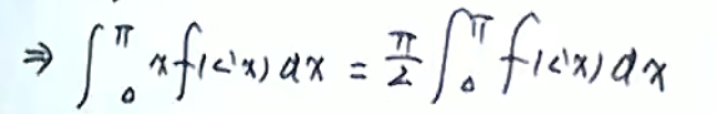
性质三
