题236.pat甲级练习-1072 Gas Station (30 分)

一、题目

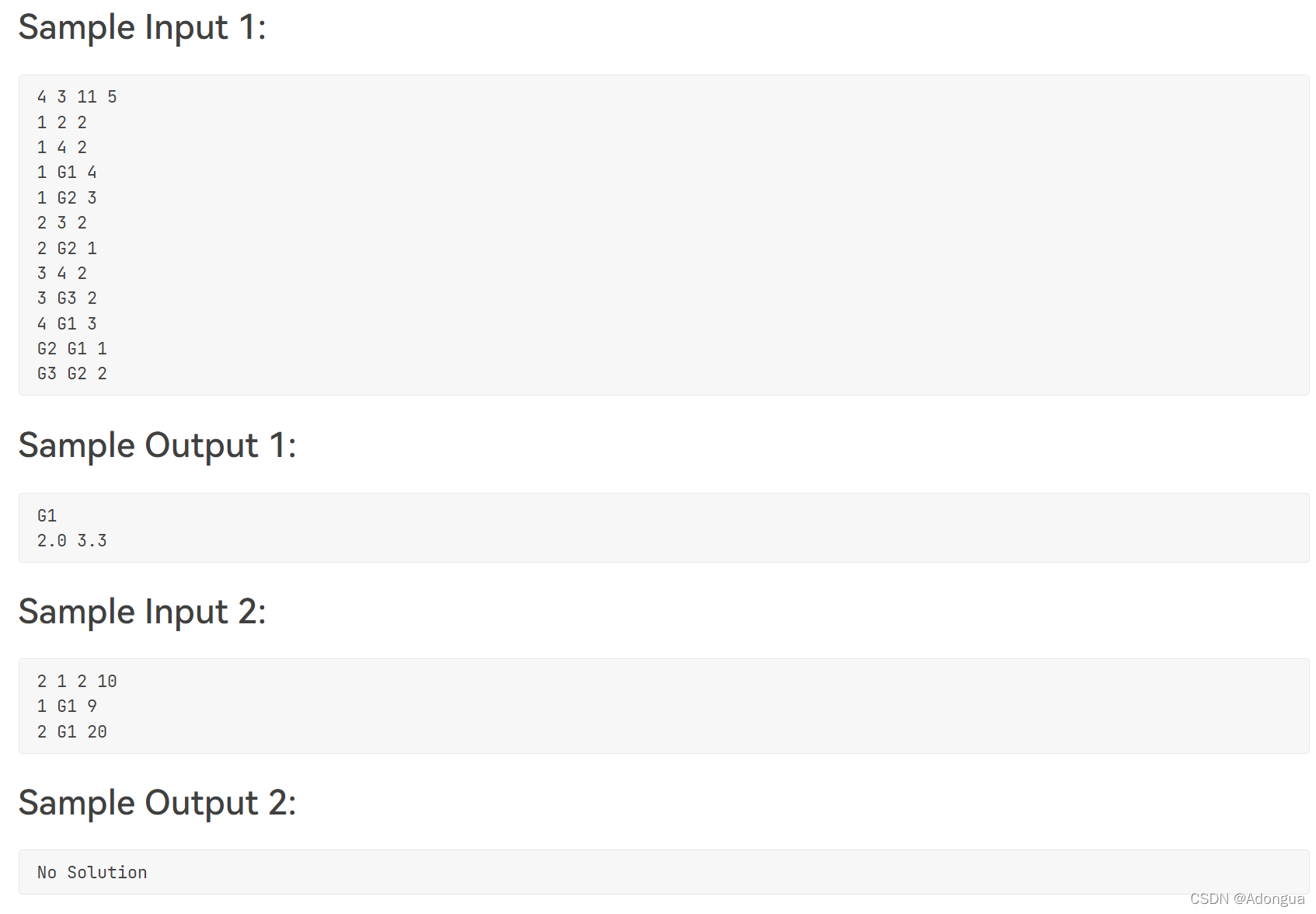
在这里插入图片描述

二、题解

本题要求得到一个最好位置的加油站，该加油站到houses的距离中的最短距离需要在所有加油站这方面中是最大的，即求最大最小距离（由题目中的这句话可以看出：A gas station has to be built at such a location that the minimum distance between the station and any of the residential housing is as far away as possible.因为我当时错解题意了，所以放在这里提醒犯病的自己。。。）。则思路如下：
①每次循环遍历加油站，先用堆优化的dijkstra求出该加油站到每个house的最短距离。
②循环遍历上述最短距离，看是否有超出服务范围的，如果有则该加油站不予考虑。上述过程中，同时去求最短的最短距离，并作求和以供后序求平均路长使用。
③每次遍历加油站的循环去求最大的最短的最短距离，更新作为答案的加油站。注意，当出现同为最大的最短的最短距离的加油站选择时再去考虑二者的平均路长，选短的作为答案。由于是从编号小的加油站开始考虑的，所以不用刻意担心平均路长相等时让编号小的加油站作为答案的情况。

#include <bits/stdc++.h>

using namespace std;

typedef pair<int,int> pii;
const int add=1000;//因为房子从1编号到1000，所以1000之后没有被编号，那就用来给加油站编号
const int maxn=add+11;//加上加油站，编号共编到1010
const int Inf=0x3f3f3f3f;

struct Node
{
    int index;
    int dist;
    bool operator < (const Node &a) const
    {
        return dist>a.dist;
    }
};

int N,M,K,Ds;
priority_queue<Node> pq;
vector<pii> G[maxn];
int collected[maxn];
int dist[maxn];
int bestpos;
double maxminpath,minaverpath=Inf;
int flag;

void Dijkstra(int s)
{
    fill(dist,dist+maxn,Inf);
    fill(collected,collected+maxn,0);
    dist[s]=0;
    pq.push(Node{s,0});
    while(!pq.empty())
    {
        int minv=pq.top().index;
        pq.pop();
        if(collected[minv])
        {
            continue;
        }
        collected[minv]=1;
        for(int i=0;i<(int)G[minv].size();i++)
        {
            int v=G[minv][i].first;
            int w=G[minv][i].second;
            if(!collected[v]&&dist[v]>dist[minv]+w)//满足松弛条件，做松弛操作，并将新权放入pq
            {
                dist[v]=dist[minv]+w;
                pq.push(Node{v,dist[v]});
            }
        }
    }
}

int main()
{
    cin>>N>>M>>K>>Ds;
    for(int i=0;i<K;i++)
    {
        int u,v,w;
        string str_u,str_v;
        cin>>str_u>>str_v>>w;
        if(str_u[0]=='G')
        {
            u=stoi(str_u.substr(1,str_u.length()-1))+add;
        }
        else
        {
            u=stoi(str_u);
        }
        if(str_v[0]=='G')
        {
            v=stoi(str_v.substr(1,str_v.length()-1))+add;
        }
        else
        {
            v=stoi(str_v);
        }
        G[u].push_back({v,w});
        G[v].push_back({u,w});
    }
    for(int i=1;i<=M;i++)
    {
        Dijkstra(i+add);
        int j;
        double pathsum=0,averpath,nowminpath=Inf;
        for(j=1;j<=N;j++)
        {
            if(dist[j]>Ds)
            {
                break;
            }
            pathsum+=dist[j];
            nowminpath=min(nowminpath,(double)dist[j]);
        }
        if(j>N)
        {
            averpath=pathsum/N;
            flag=1;
        }
        else
        {
            continue;
        }
        if(nowminpath>maxminpath)//本题要的是加油站到house中的最大最小距离，即这个最小距离要在所有的最小距离中是最大的
        {
            minaverpath=averpath;
            maxminpath=nowminpath;
            bestpos=i;
        }
        else if(nowminpath==maxminpath)
        {
            if(averpath<minaverpath)//其次考虑加油站到houses的平均距离要最小
            {
                minaverpath=averpath;
                bestpos=i;
            }
        }
    }
    if(!flag)
    {
        printf("No Solution");
    }
    else
    {
        printf("G%d\n",bestpos);
        printf("%.1lf %.1lf",maxminpath,minaverpath);
    }
}