[数据结构与算法]双指针法的应用详解

前言

通常用在线性的数据结构中，比如链表和数组。
指针其实就是数据的索引或者链表的结点。两个指针朝着左右两个方向移动，直到满足搜索条件。
双指针可分为同向双指针、异向双指针、快慢指针、滑动窗口。根据需求选择双指针的模型，比如
删除数组或链表中重复的元素，同向双指针（线性表前提是有序的）；
快慢指针一般用在链表中，比如求链表的中点、判断链表是否有环、判断链表换的起点、环的长度、以及链表的倒数第K个元素；
比如在二分查找中用的就是异向双指针；
滑动窗口其实就是在数组或者链表某个区间上的操作，比如求最长/最短子字符串或是特定子字符串的长度要求。

1.判断链表是否有环

力扣141题
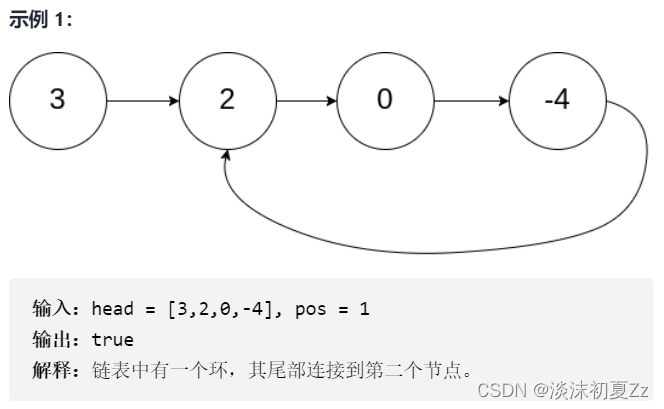
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ，则返回 true 。 否则，返回 false 。

代码实现

public class Solution {
    //快慢指针法
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode low = head;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            low = low.next;
            //此时相遇了
            if(fast == low){
                return true;
            }
        }
        return false;
    }
}

2.查找链表中间的元素

力扣876题
给定一个头结点为 head 的非空单链表，返回链表的中间结点。
如果有两个中间结点，则返回第二个中间结点。

代码实现

  //快慢指针法
    public ListNode middleNode(ListNode head) {
        ListNode low = head,fast = head;
        while(fast != null && fast.next != null){
            //慢指针走一步
            low = low.next;
            //快指针走两步
            fast = fast.next.next;
        }
        //奇数，fast.next = null时，low即为所求
        //偶数，fsat == null时，low即为所求
        return low;
    }

3.奇偶排序，前奇后偶

力扣328题
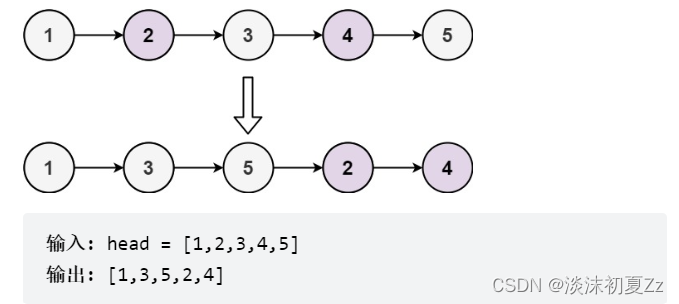
给定单链表的头节点 head ，将所有索引为奇数的节点和索引为偶数的节点分别组合在一起，然后返回重新排序的列表。
第一个节点的索引被认为是 奇数 ， 第二个节点的索引为 偶数 ，以此类推。

代码实现

 public ListNode oddEvenList(ListNode head) {
        if(head == null){
            return head;
        }
        ListNode fastHead = head.next;
        ListNode lowTail = head;//奇数链表
        ListNode fastTail = fastHead;//偶数链表
        while(fastTail != null && fastTail.next != null){
            //更新奇数节点时，奇数节点的后一个节点需要指向偶数节点的后一个节点
            lowTail.next = fastTail.next;
            lowTail = lowTail.next;
           // 更新偶数节点时，偶数节点的后一个节点需要指向奇数节点的后一个节点
            fastTail.next = lowTail.next;
            fastTail = fastTail.next;
        }
        //合并两个链表
        lowTail.next = fastHead;
        return head;
    }

4.删除排序链表的重复元素

力扣82题
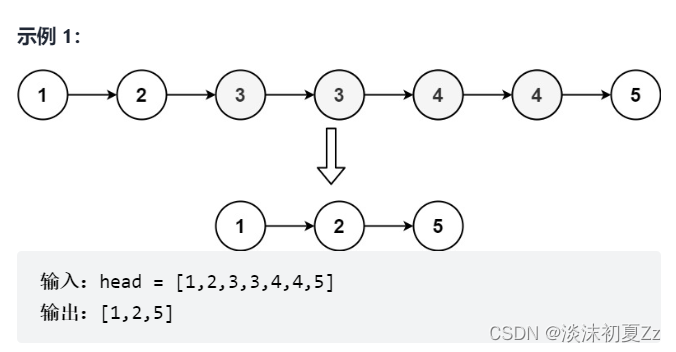
给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表

代码实现

 public ListNode deleteDuplicates(ListNode head) {
        //虚拟头节点法
        ListNode dummyHead = new ListNode(-1);
        dummyHead.next = head;
        ListNode prev = dummyHead;
        ListNode cur = prev.next;
        while(cur != null){
            //引入next指针
            ListNode next = cur.next;
            if(next == null){
                //只有一个元素
                return dummyHead.next;
            }
            if(cur.val != next.val){
                //cur不是重复节点，三指针都移动
                cur = cur.next;
                prev = prev.next;
            }else{
                //让next指针一直向后移动，直到与cur.val不相等的节点位置
                while(next != null && cur.val == next.val){
                    next = next.next;
                }
                // 此时next指向了第一个不重复的元素
                // 此时prev - next之间所有重复元素全部删除
                prev.next = next;
                cur = next;
            }
        }
        return dummyHead.next;
    }

5.三数之和

力扣15题
给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。

代码实现

 public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环
                if (second == third) {
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    List<Integer> list = new ArrayList<Integer>();
                    list.add(nums[first]);
                    list.add(nums[second]);
                    list.add(nums[third]);
                    ans.add(list);
                }
            }
        }
        return ans;
    }

6.分割链表

力扣面试题02.04
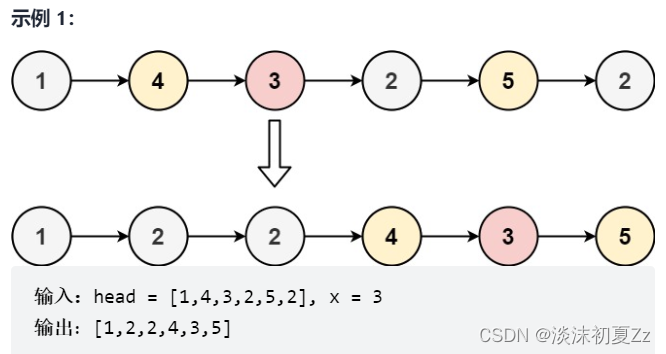
给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你不需要 保留 每个分区中各节点的初始相对位置。

代码实现

 public ListNode partition(ListNode head, int x) {
        // 创建small和big两个小链表的头节点
        ListNode smallHead = new ListNode(-1);
        ListNode bigHead = new ListNode(-1);
        // 按照升序插入，因此需要尾插
        // 分别指向两个子链表的尾部
        ListNode smallTail = smallHead;
        ListNode bigTail = bigHead;
        //遍历原链表，根据值放入small和big链表中
        while(head != null){
            if(head.val < x){
                smallTail.next = head;
                smallTail = head;
            }else{
                bigTail.next = head;
                bigTail = head;
            }
            head = head.next;
        }
        bigTail.next = null;
        //拼接小链表和大链表
        smallTail.next = bigHead.next;
        return smallHead.next;
    }

7.合并两个有序的数组

力扣88题
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。
注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

代码实现

public void merge(int[] nums1, int m, int[] nums2, int n) {
        int p1 = 0, p2 = 0;
        int[] sorted = new int[m + n];
        int cur;
        while (p1 < m || p2 < n) {
            if (p1 == m) {
                cur = nums2[p2++];
            } else if (p2 == n) {
                cur = nums1[p1++];
            } else if (nums1[p1] < nums2[p2]) {
                cur = nums1[p1++];
            } else {
                cur = nums2[p2++];
            }
            sorted[p1 + p2 - 1] = cur;
        }
        for (int i = 0; i != m + n; ++i) {
            nums1[i] = sorted[i];
        }
    }

8.两数之和—输入有序数组

力扣167题
给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

代码实现

 public int[] twoSum(int[] numbers, int target) {
        int low = 0, high = numbers.length - 1;
        while (low < high) {
            int sum = numbers[low] + numbers[high];
            if (sum == target) {
                return new int[]{low + 1, high + 1};
            } else if (sum < target) {
                ++low;
            } else {
                --high;
            }
        }
        return new int[]{-1, -1};
    }

9.长度最小的子数组

（力扣209）给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0

代码实现

//滑动窗口法
 public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = Math.min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }

10.排序链表

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

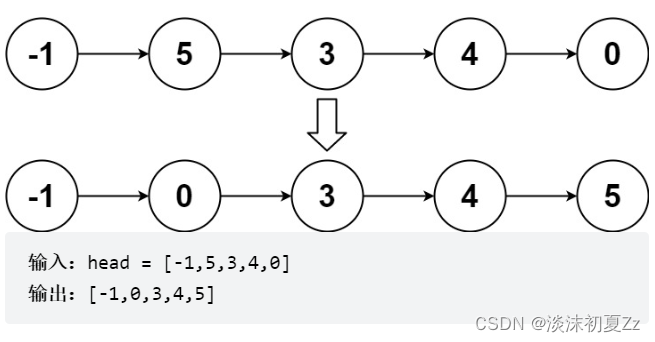
解题思路

通过递归实现链表归并排序，有以下两个环节：
🍓1，分割 cut 环节： 找到当前链表中点，并从中点将链表断开（以便在下次递归 cut 时，链表片段拥有正确边界）；
我们使用 fast,slow 快慢双指针法，奇数个节点找到中点，偶数个节点找到中心左边的节点。
找到中点 slow 后，执行 slow.next = None 将链表切断。
递归分割时，输入当前链表左端点 head 和中心节点 slow 的下一个节点 tmp(因为链表是从 slow 切断的)。
cut 递归终止条件： 当head.next == None时，说明只有一个节点了，直接返回此节点。
🍓2，合并 merge 环节： 将两个排序链表合并，转化为一个排序链表。
双指针法合并，建立辅助ListNode h 作为头部。
设置两指针 left, right 分别指向两链表头部，比较两指针处节点值大小，由小到大加入合并链表头部，指针交替前进，直至添加完两个链表。
返回辅助ListNode h 作为头部的下个节点 h.next。

代码实现

public ListNode sortList(ListNode head) {
        if (head == null || head.next == null)
            return head;
        ListNode fast = head.next, slow = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode tmp = slow.next;
        slow.next = null;
        ListNode left = sortList(head);
        ListNode right = sortList(tmp);
        ListNode h = new ListNode(0);
        ListNode res = h;
        while (left != null && right != null) {
            if (left.val < right.val) {
                h.next = left;
                left = left.next;
            } else {
                h.next = right;
                right = right.next;
            }
            h = h.next;
        }
        h.next = left != null ? left : right;
        return res.next;
    }