[数据结构与算法]从前序与中序遍历序列构造二叉树——从后序与中序序列构造二叉树

目录

一.从前序与中序遍历序列构造二叉树

题目：

分析：

代码：

二.从后序与中序遍历序列构造二叉树

题目：

分析：

代码：

一.从前序与中序遍历序列构造二叉树

题目：

?

分析：

1.从前序遍历序列可以得到：二叉树从根结点到左子树再到右子树的遍历顺序。

2.从中序遍历序列可以得到：二叉树当前结点的左右子树分别为。

3.遍历前序遍历序列，用中序遍历序列的范围表示对应的左右子树，创建二叉树，创建顺序为先左子树后右子树。

代码：

  public int preIndex = 0;
    public TreeNode createTreeByPandI(int[] preorder,int[] inorder,int inbegin,int inend) {
        if (inbegin > inend) {
            return null;
        }
        //创建根结点
        TreeNode root = new TreeNode(preorder[preIndex]);
        //找到根结点在中序遍历序列中的坐标
        int rootIndex = findIndexOfI(inorder,inbegin,inend,preorder[preIndex]);
        //排除找不到根结点的可能
        if (rootIndex == -1) return null;
        preIndex++;
        root.left = createTreeByPandI(preorder,inorder,inbegin,rootIndex - 1);
        root.right = createTreeByPandI(preorder,inorder,rootIndex + 1,inend);
        return root;
    }

    //找到根结点在中序遍历序列中的坐标
    public int findIndexOfI(int[] inorder,int inbegin,int inend,int key) {
        for (int i = inbegin;i <= inend;i ++) {
            if (inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }
    
    //带入两个序列创建二叉树
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || inorder == null) return null;
        TreeNode root = createTreeByPandI(preorder,inorder,0,inorder.length - 1);
        return root;
    }

二.从后序与中序遍历序列构造二叉树

题目：

?

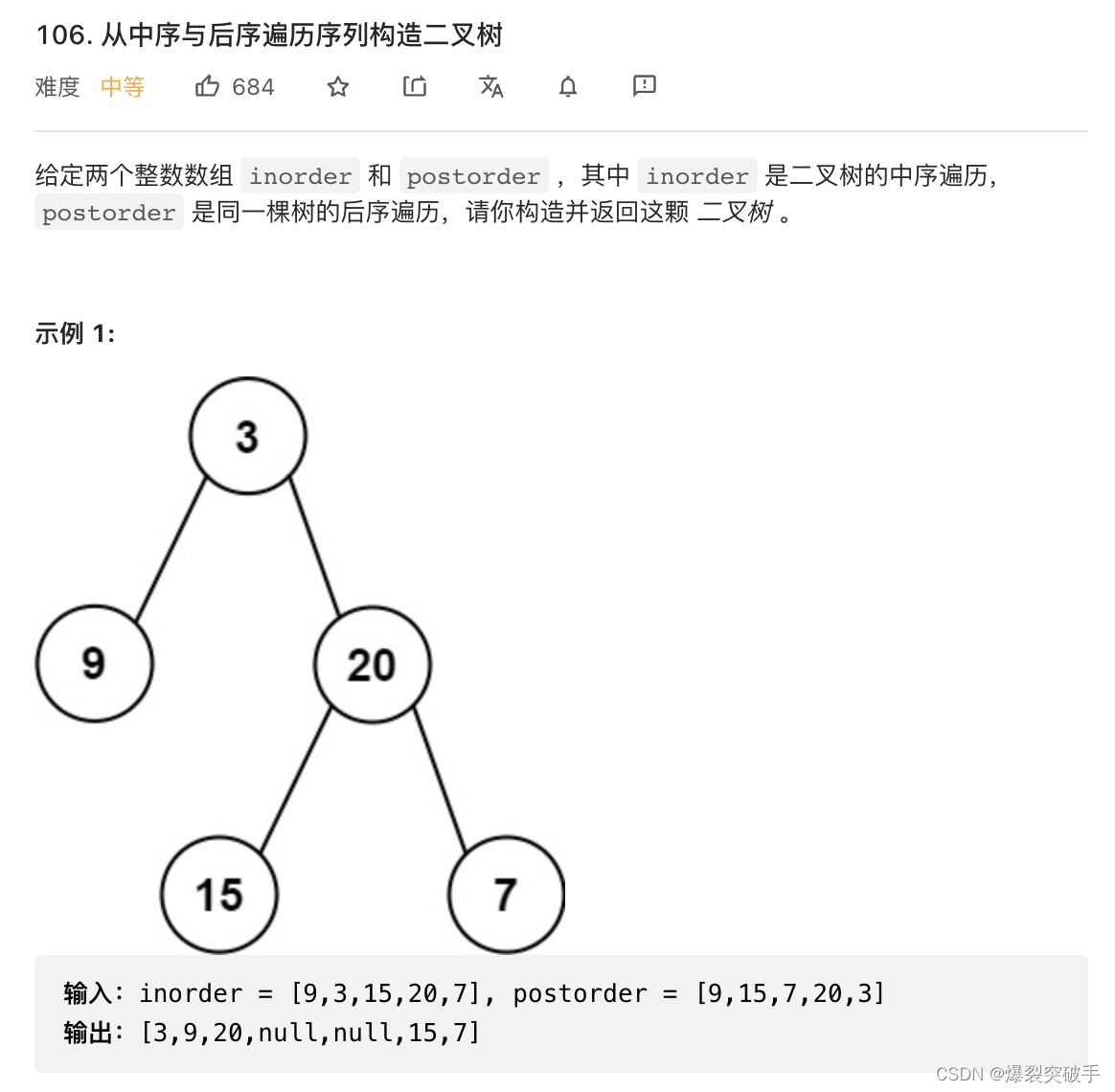
分析：

1.从后序遍历序列可以得到：二叉树从左子树到右子树再到根结点的遍历顺序。

2.从中序遍历序列可以得到：二叉树当前结点的左右子树分别为。

3.遍历后序遍历序列，用中序遍历序列的范围表示对应的左右子树，创建二叉树，创建顺序为先右子树，后左子树。

代码：

   public int postIndex = 0;
    public TreeNode createTree(int[] inorder,int[] postorder,int inbegin,int inend) {
        if (inend < inbegin) return null;
        //创建结点
        TreeNode root = new TreeNode(postorder[postIndex]);
        //找到该结点在中序遍历序列当中的坐标
        int rootIndex = findIndexOfI(inorder,inbegin,inend,postorder[postIndex]);
        //排除找不到结点的可能
        if (rootIndex == -1) {
            return null;
        }
        postIndex--;
        root.right = createTree(inorder,postorder,rootIndex + 1,inend);
        root.left = createTree(inorder,postorder,inbegin,rootIndex - 1);
        return root;
    }
    //根据该结点的值找到其在中序遍历序列当中的坐标
    public int findIndexOfI(int[] inorder,int inbegin,int inend,int key) {
        for (int i = inbegin;i <= inend;i++) {
            if (inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }

    //带入两个序列创建二叉树
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if (inorder == null || postorder == null) return null;
        postIndex = postorder.length - 1;
        TreeNode root = createTree(inorder,postorder,0,inorder.length - 1);
        return root;
    }