前言
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
可以这样:
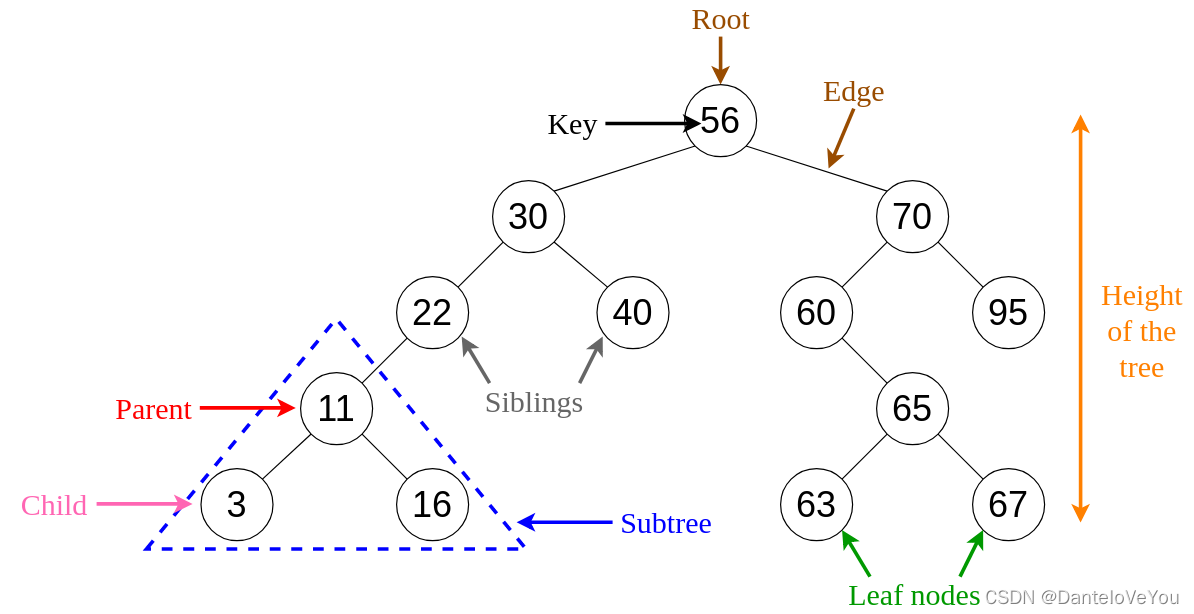
这样:
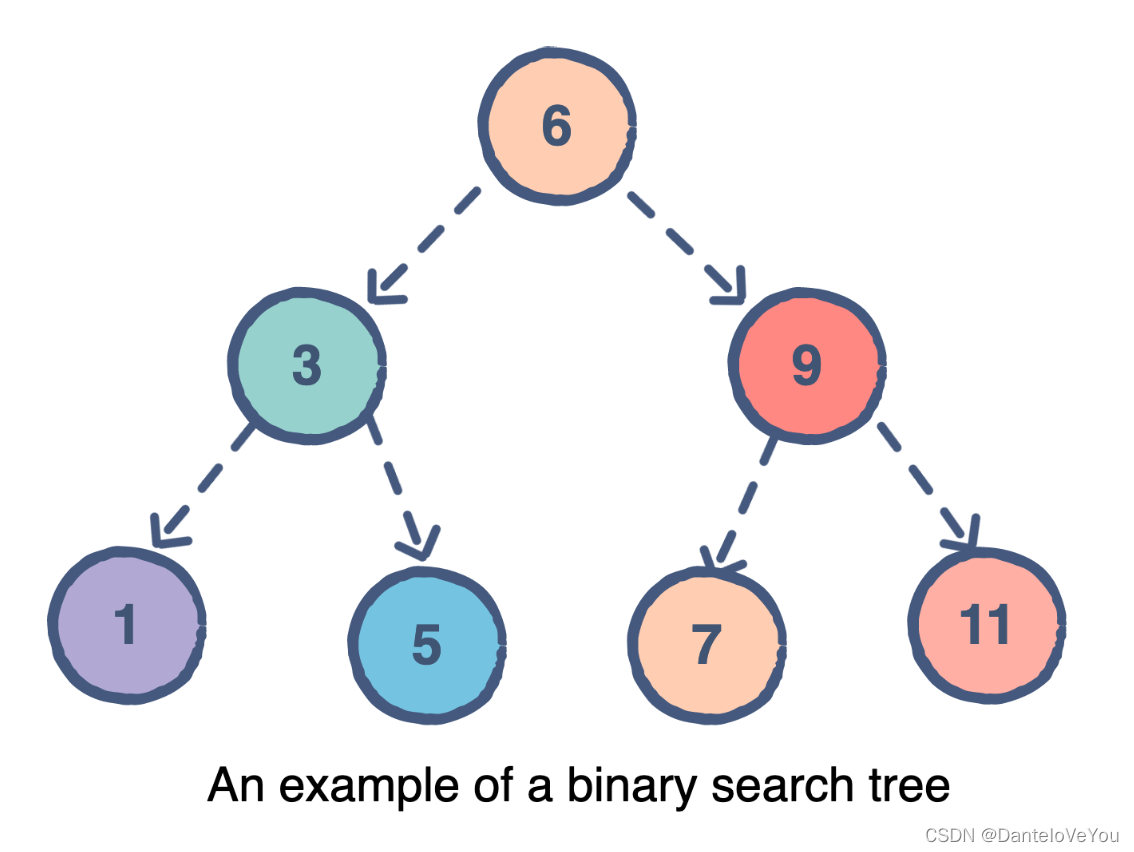
或者这样:

可以看到的是,一般的二叉搜索树形态各异,因为只有以下的约束条件:
- 左子树比根小
- 右子树比根大
分析一下性能:
- 最优情况下,二叉搜索树为完全二叉树,其平均比较次数为:log(N)
- 最差情况下,二叉搜索树退化为单支树,其平均比较次数为:N/2
节点的插入操作
插入一个节点,只需要满足插入后:
- 左子树比根小
- 右子树比根大
新插入的节点一定会成为叶子节点
在这里,我们约定每个节点的值都不相同,也就是说不能出现值重复的节点
我们需要一个parent来连结新插入的节点与原来的树:
bool Insert(K key) {
if (_root == nullptr) {
_root = new Node(key);
}
else {
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
return false;
}
}
cur = new Node(key);
if (key < parent->_key) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
}
return true;
}
节点的删除操作
删除一个节点,相较插入略显复杂,请看以下三种情形:
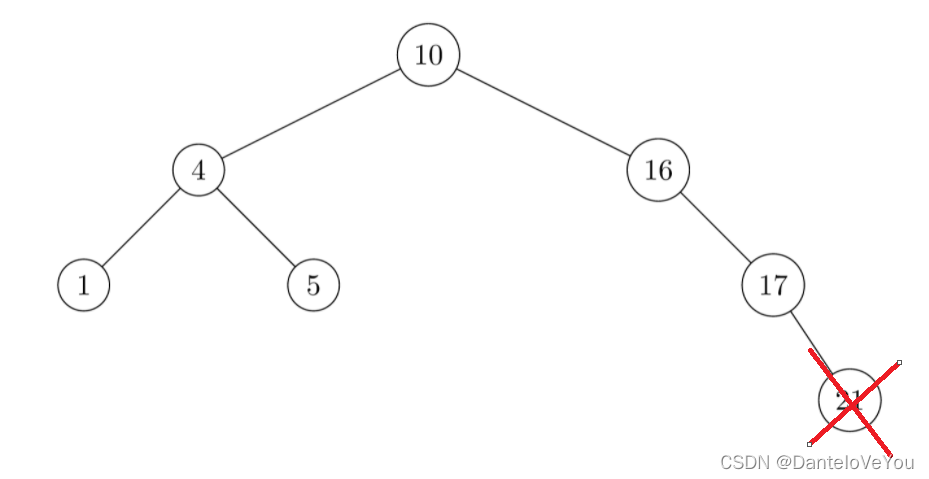
1.删除叶子节点
这个简单,删了叶子节点对父节点没有半毛钱的影响,不需要调整,直接删就行
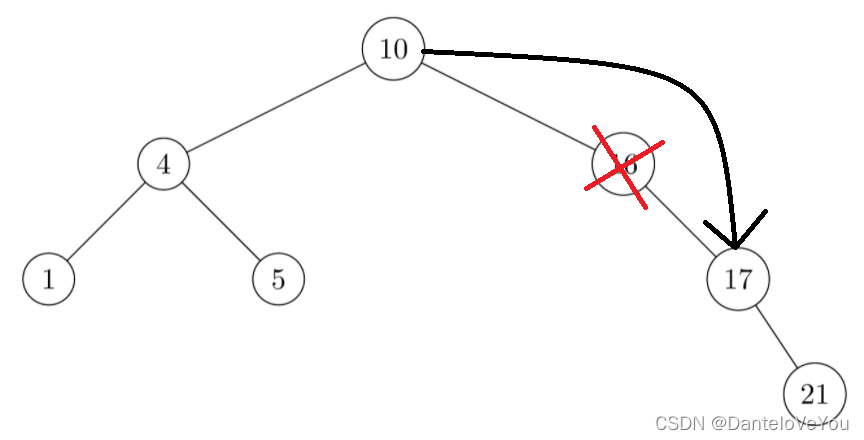
2.删除的节点只有左孩子或只有右孩子
这个也简单,删了节点之后只要把父节点与单支子树连起来就行
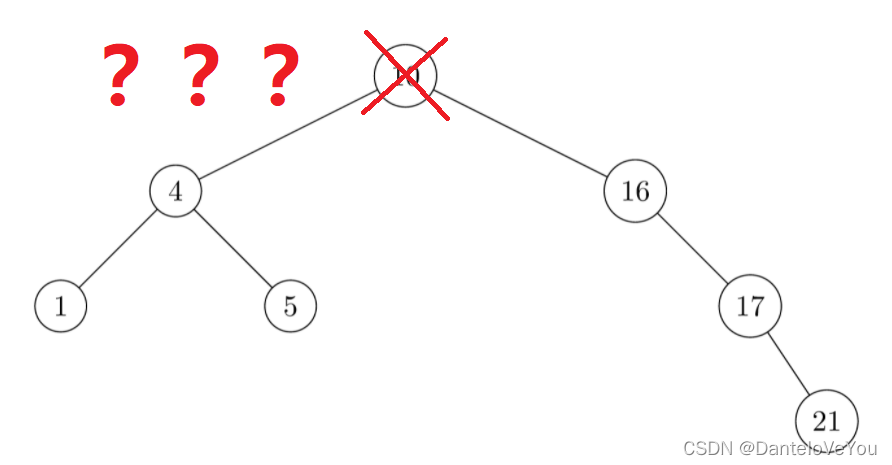
3.删除的节点左右孩子都存在
这个有点难度,删了节点之后,得调整树了
可以采用替换法来解决:
1.删除是把原来的节点上的值覆盖掉,那么我们就直接拿一个特殊节点的值来替代这个删除节点的值
2.替换后,那个特殊节点会被干掉,所以选取特殊节点的时候,它越好被干掉,越适合
3.谁最好被干掉?当然是前两种情况啦
4.我们选取一个合适的叶子节点来替代被删除节点的位置,替换后,树仍为二叉搜索树
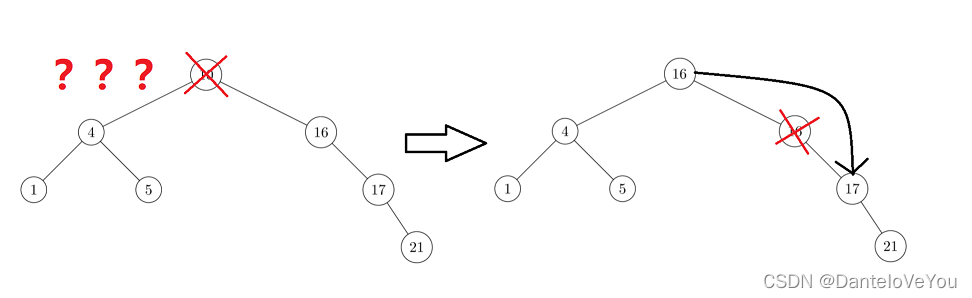
5.所以,我们可以把待删节点当作根,选取它左子树的最大或者右子树的最小来替代待删节点
以右子树最小举例:
当然这边的右子树是单支树,所以最小正好是右孩子,若不是单支树,则是右子树的最左节点
bool Erase(K key) {
// 5
// 3 7
// 1 4 6 8
//0 2 9
// 叶子
// 只有一个孩子
// 有两个孩子
Node* parent = _root;
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr) {
// 左孩子为空
// 1. cur为根
if (cur == _root) {
_root = cur->_right;
}
// 2. cur不为根
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr) {
// 右孩子为空
// 1. cur为根
if (cur == _root) {
_root = cur->_left;
}
// 2. cur不为根
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else {
// 左右孩子都不为空
Node* RLNode = cur->_right;
Node* pRLNode = cur;
Node* ppRLNode = cur;
while (RLNode) {
ppRLNode = pRLNode;
pRLNode = RLNode;
RLNode = RLNode->_left;
}
cur->_key = pRLNode->_key;
if (ppRLNode->_left == pRLNode) {
ppRLNode->_left = pRLNode->_right;
}
else {
ppRLNode->_right = pRLNode->_right;
}
delete pRLNode;
pRLNode = nullptr;
}
return true;
}
}
return false;
}
代码
namespace K {
template<class K>
struct BSTreeNode {
K _key;
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
BSTreeNode(K key)
:_key(key)
, _left(nullptr)
, _right(nullptr) {}
~BSTreeNode() {
//delete
//cout << _key << endl;
}
};
template <class K>
class BSTree {
public:
typedef BSTreeNode<K> Node;
BSTree()
:_root(nullptr) {}
bool Insert(K key) {
if (_root == nullptr) {
_root = new Node(key);
}
else {
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
return false;
}
}
cur = new Node(key);
if (key < parent->_key) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
}
return true;
}
Node* Find(K key) {
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
cur = cur->_left;
}
else if (key > cur->_key) {
cur = cur->_right;
}
else {
return cur;
}
}
return nullptr;
}
bool Erase(K key) {
// 5
// 3 7
// 1 4 6 8
//0 2 9
// 叶子
// 只有一个孩子
// 有两个孩子
Node* parent = _root;
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr) {
// 左孩子为空
// 1. cur为根
if (cur == _root) {
_root = cur->_right;
}
// 2. cur不为根
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr) {
// 右孩子为空
// 1. cur为根
if (cur == _root) {
_root = cur->_left;
}
// 2. cur不为根
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else {
// 左右孩子都不为空
Node* RLNode = cur->_right;
Node* pRLNode = cur;
Node* ppRLNode = cur;
while (RLNode) {
ppRLNode = pRLNode;
pRLNode = RLNode;
RLNode = RLNode->_left;
}
cur->_key = pRLNode->_key;
if (ppRLNode->_left == pRLNode) {
ppRLNode->_left = pRLNode->_right;
}
else {
ppRLNode->_right = pRLNode->_right;
}
delete pRLNode;
pRLNode = nullptr;
}
return true;
}
}
return false;
}
void InOrder() {
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root) {
if (root != nullptr) {
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
}
private:
Node* _root;
};
}
namespace KV {
template<class K, class V>
struct BSTreeNode {
K _key;
V _val;
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
BSTreeNode(K key, V val)
:_key(key)
, _val(val)
, _left(nullptr)
, _right(nullptr) {}
~BSTreeNode() {
}
};
template <class K, class V>
class BSTree {
public:
typedef BSTreeNode<K, V> Node;
BSTree()
:_root(nullptr) {}
V& operator[](K key) {
pair<Node*, bool> ret = Insert(key, V());
return ret.first->_val;
}
pair<Node*, bool> Insert(K key, V val) {
if (_root == nullptr) {
_root = new Node(key, val);
return make_pair(_root, true);
}
else {
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key> cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
return make_pair(cur, false);
}
}
cur = new Node(key, val);
if (key < parent->_key) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
return make_pair(cur, true);
}
}
Node* Find(K key) {
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
cur = cur->_left;
}
else if (key > cur->_key) {
cur = cur->_right;
}
else {
return cur;
}
}
return nullptr;
}
bool Erase(K key) {
// 5
// 3 7
// 1 4 6 8
//0 2 9
// 叶子
// 只有一个孩子
// 有两个孩子
Node* parent = _root;
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr) {
// 左孩子为空
// 1. cur为根
if (cur == _root) {
_root = cur->_right;
}
// 2. cur不为根
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr) {
// 右孩子为空
// 1. cur为根
if (cur == _root) {
_root = cur->_left;
}
// 2. cur不为根
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else {
// 左右孩子都不为空
Node* RLNode = cur->_right;
Node* pRLNode = cur;
Node* ppRLNode = cur;
while (RLNode) {
ppRLNode = pRLNode;
pRLNode = RLNode;
RLNode = RLNode->_left;
}
cur->_key = pRLNode->_key;
cur->_val = pRLNode->_val;
if (ppRLNode->_left == pRLNode) {
ppRLNode->_left = pRLNode->_right;
}
else {
ppRLNode->_right = pRLNode->_right;
}
delete pRLNode;
pRLNode = nullptr;
}
return true;
}
}
return false;
}
void InOrder() {
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root) {
if (root != nullptr) {
_InOrder(root->_left);
cout << root->_key << ":" << root->_val << " ";
_InOrder(root->_right);
}
}
private:
Node* _root;
};
}