写在前面
小伙伴们我们又见面啦~这篇文章拖了又拖,终于写完啦。这篇讲了几道蓝桥杯中考察DFS和BFS的真题,大家可以去看看前面两篇文章,对搜索讲的很详细。【一万字】蓝桥杯算法竞赛备考(一)——搜索专题(上)(C++) 以及 蓝桥杯算法竞赛备考(一)—— 搜索专题(下)(C++) 。
好啦废话不多说进入今天的学习~

一、搜索思想的总结

这是洛谷对DFS和BFS搜索的总结。正是由于这两种搜索算法的特性,使得它比暴力枚举的效率高,可以处理些数据规模小的题目,一些数据规模大的就要剪枝优化或者寻找其他高效的算法。
| DFS | BFS |
|---|---|
| 适合求方案总数 | 适合求解最短路,连通性问题 |
| 利用递归来实现 | 利用队列1来实现 |
| 试探搜索 | 地毯搜索 |
| 沿着一条路走到黑 | 总是先w试距离初始状态最近的状态 |
大家可以按照我写的这个题单来做题噢~看看自己是不是掌握了DFS和BFS。

二、蓝桥杯真题(搜索算法)
1. 2017-试题D 方格分割
题目链接

题目分析
首先我们要考虑这样一个问题,怎样才能使剪成的这两部分的形状是完全一样的。
这两部分一定是关于中心对称的。如果发现了这样一个规律,那么这个问题的思路也就清晰明了了。
我们从中心点(3,3)出发,向上,下,左,右四个方向进行DFS搜索,当到达边界时说明一条分割方案就形成了。然后回溯继续寻找下一个分割方案。当然还有一些细节需要注意。
- 当一个点
(x, y)被搜索的时候,它的中心对称点(6 - x, 6 - y)就也就不能被搜索。因此需要标记两个点,即maze[x][y] = 1和maze[6 - x][6 - y] = 1。(表示该点已经访问过了)
对称点为啥是(6 - x, 6 - y),小伙伴们画下图看一看就明白了~
- 由于题目中说旋转对称属于同一种割法,那么一种分割方案绕着中心点顺时针旋转得到的方案和原来的方案是同一种。因此我们在
DFS完之后的ans要除以4。
AC代码
//2017 方格分割
#include <iostream>
#include <cstring>
using namespace std;
int maze[7][7];//表示格子的点,maze[x][y] = 1表示该点已访问.
int dx[4] = {0, -1, 1, 0};
int dy[4] = {-1, 0, 0, 1};//偏移量
int ans;
void dfs(int x, int y)
{
if (x == 0 || x == 6 || y == 0 || y == 6)//到达边界ans+1
{
ans++;
return;
}
for (int i = 0; i < 4; i++)//沿着四个方向进行搜索
{
int x1 = x + dx[i];
int y1 = y + dy[i];
if (maze[x1][y1] != 1)//没有被访问
{
maze[x1][y1] = 1;
maze[6 - x1][6 - y1] = 1;//将该点和其对称点设置成已访问
dfs(x1, y1);
maze[x1][y1] = 0;
maze[6 - x1][6 - y1] = 0;//回溯,还原现场
}
}
}
int main()
{
maze[3][3] = 1;//开始的时候要将中心点设置成已访问。
dfs(3, 3);
cout << ans / 4 << endl;//旋转对称属于同一种分割方案
return 0;
}
2. 2019-试题A 组队
题目链接


题目分析
这道题是填空题,问评分之和最大可能是多少,由于该题的数据量不大,我们完全可以手算。
另外这道题是一道典型的DFS问题,对于一号位来说,它有20种选择,而对于二号位来说,它有除一号位选择的球员外的19种选择,以此类推。那么DFS的思路也就很明确了。我们从一号位开始DFS,维护当前正在选择的第index位,以及当前的评分之和sum。当1~5号位都DFS完,用maxsum来更新最大的评分之和。
总结一下这道题有两种解法:
- DFS搜索(准确)
- 观察+手算(最快)
Answer 1. DFS
#include <iostream>
using namespace std;
int maxsum;
int maze[20][5];
bool visited[20];
void dfs(int index, int sum)
{
if (index == 5)//5号位处理完
{
maxsum = max(maxsum, sum);//更新最大评分之和
return;
}
for (int i = 0; i < 20; i++)
{
if (maze[i][index] != 0 && visited[i]== false)
{
visited[i] = true;
dfs(index + 1, sum + maze[i][index]);
visited[i] = false;
}
}
}
int main()
{
for (int i = 0; i < 20; i++)
{
for (int j = 0; j < 5; j++)
{
cin >> maze[i][j];
}
}
dfs(0, 0);
cout << maxsum;
return 0;
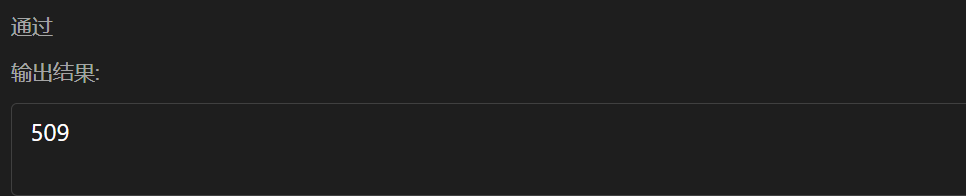
//maxsum = 490
}

Answer 2. 观察+手算
很容易就可以发现评分之和最大是多少,这里就不详细展开说了。
3. 2018-试题I 全球变暖
题目链接


题目分析
- 怎么判断某块陆地是否被淹没——这块陆地的上下左右四个方向都是陆地,那么该块陆地就不会被淹没,否则被淹没。
- 被完全淹没的岛屿数 = 淹没前的岛屿数ans1 - 淹没后的岛屿数ans2。
- 通过DFS搜索找到一块岛屿,并将其陆地都标记下来,防止重复搜索。并且找到满足不被淹没的陆地,
ans2++。
这道题思路不是太难,具体细节可以看下代码的注释噢~
AC代码
#include <iostream>
using namespace std;
const int N = 1010;
char maze[N][N];
int ans1, ans2;
bool flag;
int n;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
bool check(int x, int y)
{
if (maze[x][y] == '.') return false;
if (x < 0 || x >= n || y < 0 || y >= n) return false;
return true;
}
void dfs(int x, int y)
{
// if (maze[x][y] != '#') return;
int ans = 0;
if (!flag)//没找到满足条件的陆地
{
for (int i = 0; i < 4; i++)//目的是查找有没有陆地周围有四个陆地
{
int x1 = x + dx[i];
int y1 = y + dy[i];
if (check(x1, y1))
{
ans++;
}
}
}
if (ans == 4)
{
ans2++;
flag = true;//找到满足条件的陆地flag设为true
}
maze[x][y] = '*';//将访问过的陆地设成*,防止重复访问
for (int i = 0; i < 4; i++)
{
int x1 = x + dx[i];
int y1 = y + dy[i];
if (check(x1, y1) && maze[x1][y1] != '*')
{
dfs(x1, y1);
}
}
}//一次dfs就能找到一个连通块,也就是一个岛屿
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> maze[i];
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (maze[i][j] == '#')//只有在为陆地的时候才进行搜索
{
ans1++;//dfs几次就得到几个岛屿
dfs(i, j);
flag = false;//记得DFS完一个岛屿后要将flag还原
}
}
}
cout << ans1 - ans2 << endl;
return 0;
}

当然这道题同样可以用BFS来实现,小伙伴们可以动手做一下,加深对DFS和BFS的理解。
4. 2019-试题E 迷宫
题目链接


题目分析
这道题和蓝桥杯算法竞赛备考(一)—— 搜索专题(下)(C++)中的迷宫最短路问题是类似的,只不过这道题还要记录一下搜索的路径,输出字典序最小的那条路径。
怎么保证输出的是字典序最小的路径呢,我们只需要在搜索的过程中按照DLRU的顺序来搜索,最终得到的最短路径一定是字典序最小的。为此我们要设置方向数组。
int dx[4] = {1, 0, 0, -1};int dy[4] = {0, -1, 1, 0};
(1,0)表示往下走,(0,-1)表示往左走,(0,1)表示往右走,(-1,0)表示往上走。咦~等一下,爱思考的小伙伴们应该已经发现了有些不对劲,这方向数组设的不对劲呀,(-1,0)明明是往下走,怎么会是往上呢?这几个根本对不起来阿。别慌,我给大家画个图就明白了。

看了这个图,小伙伴们应该也就明白了,我们不能用传统的方向数组来表示这道题,这是这道题的一个坑,实话实说我开始也卡在了这里。
设置一个结构体,里面储存点的坐标以及步数还有记录到达该点的路径。
struct node
{
int x;
int y;
int step;
string ans;
}
在搜索的过程中,记录到达该点的路径,我们可以设置个dic数组,代表DLRU。将某点入队时,Node.ans = temp.ans + dic[i];。
然后其他的地方直接套模板就好啦~
AC代码
#include <iostream>
#include <queue>
#include <string>
using namespace std;
//DLRU
// int dx[4] = {0, -1, 1, 0};
// int dy[4] = {-1, 0, 0, 1};
int dx[4] = {1, 0, 0, -1};
int dy[4] = {0, -1, 1, 0};
bool inq[55][55];
char maze[55][55];
char dic[4] = {'D', 'L', 'R', 'U'};
struct node
{
int x;
int y;
int step;
string ans;
}s, t, Node;
bool check(int x, int y)
{
if (x < 0 || x >= 30 || y < 0 || y >= 50) return false;
if (inq[x][y]) return false;
if (maze[x][y] == '1') return false;
return true;
}
void bfs()
{
queue<node> q;
q.push(s);
inq[s.x][s.y] = true;
while (!q.empty())
{
node temp = q.front();
q.pop();
if (temp.x == t.x && temp.y == t.y)
{
cout << temp.step << endl << temp.ans;
return;
}
for (int i = 0; i < 4; i++)
{
int x1 = temp.x + dx[i];
int y1 = temp.y + dy[i];
if (check(x1, y1))
{
Node.x = x1;
Node.y = y1;//开始忘记给Node的x,y赋值,一直出不来结果。
Node.step = temp.step + 1;
Node.ans = temp.ans + dic[i];
q.push(Node);
inq[x1][y1] = true;
}
}
}
}
int main()
{
for (int i = 0; i < 30; i++)
{
for (int j = 0; j < 50; j++)
{
maze[i][j] = getchar();
}
getchar();//消耗掉回车
}
s.x = 0, s.y = 0, s.step = 0, s.ans = "";
t.x = 29, t.y = 49;
bfs();
return 0;
}
//186
//DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRD//DDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDD//LLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR


写在后面
对搜索的讲解就要告一段落了,接下来我会写几篇关于动态规划的文章,去年小伙伴们也发现了,蓝桥杯对DP思想的考查力度加大了,DP和搜索一样也是我们备考的重点。小伙伴们可以期待一下。下一篇文章三天就可以写完啦
创作不易,小伙伴们一键三连关注一下吧~

