排序算法根据数据是否存在内存中进行排序,划分为内部排序和外部排序。
而常见的内部排序算法有十种,又可根据是否需要进行元素的比较,划分为比较类排序和非比较类排序。


插入排序
简单插入排序
玩扑克牌时最常用的就是简单插入排序

摸一张牌插入已经有序的队列中,将这张牌依次与队列中的牌比较,左边比它小右边比它大则插入该位置。
插入排序:插入排序基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序。
插入排序的基本思想是:每次将一个待排序的数据,按其关键码值的大小插入前面已经排序的数据中的适当位置上,直到全部插入完为止。
单趟插入排序(升序)示例:



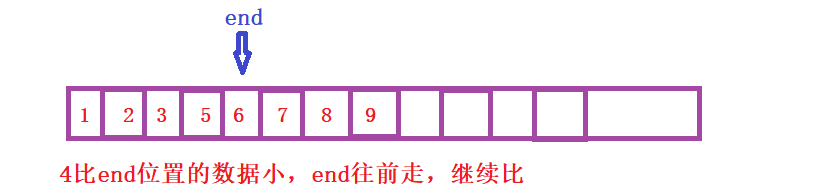



但是大多数情况我们面临的环境,都是给你一段无序的数据要求你进行排序。
基于上面单趟排序的思想,可以将数组的第一个数据当作是一个有序的数组,其后面的一个元素当作要插入这个有序的数组的元素,插入之后又是一个有序的数组,按照这个思路依次进行插入,直到最后一个元素插入完成为止。这里可能有一点绕,但是原理是很简单的。
插入排序(升序)动图演示如下:

【参考代码】
//直接插入排序(升序为例)
void InsertSort(int* arr, int n)
{
assert(arr); //防止传一个空的数组
int i = 0;
for (i = 0; i < n - 1; i++) //注意是小于n-1,因为最后一个数据当作插入的数据
{
int end = i;
int x = arr[end + 1]; //其后的一个数据当作要插入的数据
while (end >= 0)
{
if (arr[end] > x)
{
arr[end + 1] = arr[end];//将end的数据往后移,以便之后的插入,不用担心数据被覆盖,因为之前已经存放在x里了
--end;
}
else
{
break; //找到合适的位置,跳出
}
}
arr[end + 1] = x; //插入
}
}
复杂度
时间复杂度
- 最坏时间复杂度:O(n^2), 逆序为最坏情况。
- 最好时间复杂度:O(n) , 接近有序为最好情况。
空间复杂度
- O(1), 并没有借助额外的空间。
希尔排序
希尔排序又可称为“缩小增量排序”,它优化了简单插入排序。
根据上面对简单插入排序的探讨,当序列接近有序时,时间复杂度可达到O(n).
希尔排序的思想:首先使得整个序列接近有序后,最后在使用简单插入排序。为了使得整个序列接近有序采用了分组预排序的方法,取某个固定距离的数据为一组进行分组。

此时该序列已经相较与之前更接近有序了,再减少距离来分组排序则更接近有序。
其实在分组的时候取多少为间距并没有给出明确的规定,一般是先采用序列的一半为距离,后面依次缩小一半的距离进行多次分组预排序,所以希尔排序又可称为“缩小增量排序”。当距离为1时其实就是一次直接插入排序。
我们先来实现以gap为距离分一次组的预排序。
//希尔排序,一次分组预排序
void ShellSort_One(int* arr, int n)
{
assert(arr);
int i = 0;
int j = 0;
int gap = 3;
for (j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
int end = i;
int x = arr[end + gap];
while (end >= 0)
{
if (arr[end] > x)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = x;
}
}
}
以上面的例子进行测试,答案一致。

而多次分组预排序即可达到目的。
//希尔排序,版本一
void ShellSort_One(int* arr, int n)
{
assert(arr);
int i = 0;
int j = 0;
int gap = n;
while (gap > 0)
{
gap /= 2; //上面已经解释过这里为什么是除以2
for (j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
int end = i;
int x = arr[end + gap];
while (end >= 0)
{
if (arr[end] > x)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = x;
}
}
}
}
【优化】
上面的思路,我们采用的一次分组预排序是:每组各自进行排序,一组排好序之后再排下一组”。其实我们还可以采用:每组交替进行一次插入排序,直到达到目的,可以理解为“一锅炖”。
//希尔排序,版本二
void ShellSort_Two(int* arr, int n)
{
int i = 0;
int gap = n;
while (gap > 1)
{
gap /= 2;
for (i = 0; i < n - gap; ++i)
{
int end = i;
int x = arr[end + gap];
while (end >= 0)
{
if (arr[end] > x)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = x;
}
}
}
选择排序
简单选择排序
【简述】
选择排序的思想:先以第一个数为参照数,在后面剩下的序列中选出比它小并且是剩下的序列中最小的数,将这个数与参照数的位置交换。此时属于第一个位置的数已经排好,剩下的数依次按照这个方法进行直到达到排序的目标。
【动图如下】

那么我们来实现一下。
//简单选择排序
//版本一
void SelectSort(int* arr, int n)
{
assert(arr);
int begin = 0;
while (begin < n)
{
int MinIndex = begin;
for (int i = begin; i < n; i++)
{
//如果小于当前要参考的数据,则先交换下标
if (arr[i] < arr[MinIndex])
{
MinIndex = i;
}
}
Swap(&arr[begin], &arr[MinIndex]);
++begin;
}
}
【优化】
这个思路还可以再优化,如何再进行优化?
以排升序为例子。也即是右边的位置可以同时选出剩下序列中最大的数进行交换
//简单选择排序
//版本二
void SelectSort(int* arr, int n)
{
assert(arr);
int begin = 0, end = n - 1;
//当左右相遇或错开时则说明已经排好序
while (begin < end)
{
int MinIndex = begin, MaxIndex = end; //相对最小和相对最大的数的下标
for (int i = begin; i <= end; i++)
{
if (arr[MinIndex] > arr[i])
{
MinIndex = i;
}
if (arr[MaxIndex] < arr[i])
{
MaxIndex = i;
}
}
Swap(&arr[begin], &arr[MinIndex]);
//调整
if (begin == MaxIndex)
{
MaxIndex = MinIndex;
}
Swap(&arr[end], &arr[MaxIndex]);
++begin;
--end;
}
复杂度
- 时间复杂度:O(N^2),最好情况和最坏情况都是O(n ^ 2 )。
- 空间复杂度:O(1),没有借助额外空间。
堆排序
参考博文堆排序
交换排序
冒泡排序
【简述】
冒泡排序的思想就是,重复地走访要排序的序列,依次比较两个相邻的元素,如果顺序错误就把他们交换过来。直到达到排序的目标,这个过程就像大的气泡不断地向上冒出,因此被称作“冒泡排序”。
【动图】

【参考代码】
//冒泡排序,排升序为例
void BubbleSort(int* arr, int n)
{
assert(arr);
int i = 0;
int j = 0;
for (j = 0; j < n - 1; j++)
{
for (i = 0; i < n - j - 1; i++)
{
if (arr[i] > arr[i + 1])
{
Swap(&arr[i], &arr[i + 1]);
}
}
}
}
快速排序
【简述】
1960年,Hoare进入Elliott兄弟伦敦公司,成为一名程序员。他接到的第一个任务,就是为Elliott 803计算机编写一个库程序,实现新发明出来的Shell排序算法。在此过程中,Hoare对不断提升代码的效率着了迷。他不仅很好地完成了任务,还发明了一种新算法,比Shell还快,而且不会多耗费太多空间。这就是后来闻名于世的快速排序算法Quicksort。
快速排序的思想:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
据我所知,直到现在快速排序有了多种版本的实现,但是其思想都是基于Hoare版本的。例如:挖坑版本和双指版本。
Hoare版本
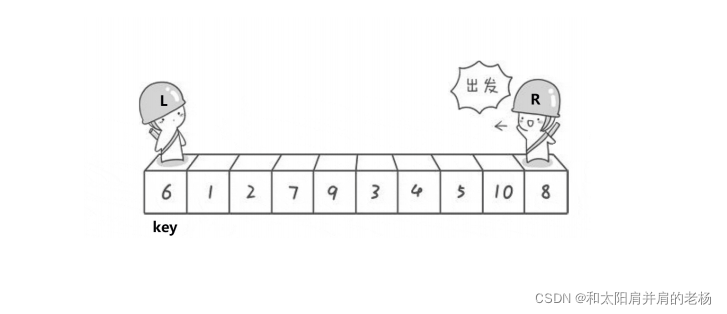
通俗一点特来描述,就是找到key在排好序后真实所在的位置。
以排升序为例,假设以第一个为基准值key:
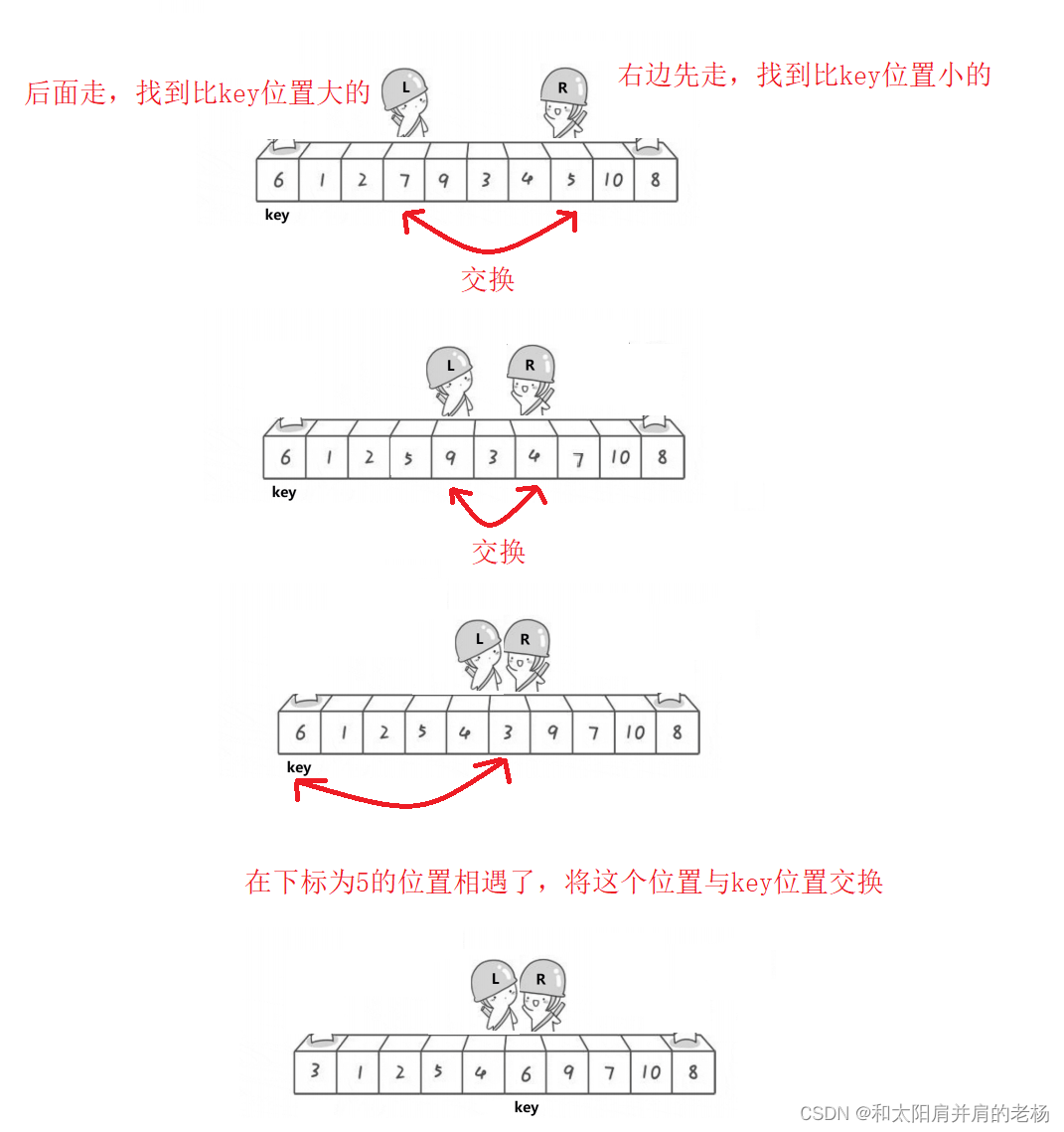
此时意味着如果该序列在排好升序后,key此时的位置就是它排序后所在的真实位置。
【注意】
- 排升序如果以左边为基准值,那么应该先从右边选出比它小的值,再从左边选出比它大的值,两者交换。
- 排升序如果以右边为基准值,那么应该先从左边选出比它小的值,再从右边选出比它大的值,两者交换。
- 排降序则规则相反。
根据探讨,只需要将待排序的序列中每一个值都放置在其排序后所属的真实位置,那么整个序列就排好序了。因此我们将采用递归方法,类似于二叉树的结构来实现该思路。
【参考代码】
//单趟
int partion(int* arr, int left, int right)
{
assert(arr);
int key = left;
//当左右还未相撞时
while (left < right)
{
//从右边找到比key小的值,然后等左边找到比key大的值
while (left < right && arr[key] < arr[right])
{
--right;
}
//从左边找到比key大的值
while (left < right && arr[key] > arr[left])
{
++left;
}
//两边都找到后,交换
Swap(&arr[left], &arr[right]);
}
//相遇后,与key位置的值交换
Swap(&arr[key], &arr[left]);
return left;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
assert(arr);
if (left > right)
{
return;
}
int keyIndex = partion(arr, left, right); //key位置的值排好序后的真实下标
//排左边
QuickSort(arr, left, keyIndex - 1);
//排右边
QuickSort(arr, keyIndex + 1, right);
}
但是这样的代码却存在很大的毛病,我们采用了递归,然而如果我们选取的key是最小的,那么递归的深度就会比较深,栈则会溢出。因此我们要优化一下此代码。
【优化】
为了使得所使用的key的值比较适当,我们将采取三数取中法。也就是在最左边,中间,以及最右边,这三个数中选取数值为中间的数来调整为key的值。
//三数取中->找到三个数中,数值大小为中间的数
int GetMin(int* arr, int left, int right)
{
int midIndex = (left + right) / 2;
if (arr[midIndex] > arr[left] )
{
if (arr[right] > arr[midIndex])
{
return midIndex;
}
else if(arr[left] > arr[right])
{
return left;
}
else
{
return right;
}
}
else //arr[left] > arr[midIndex]
{
if (arr[right] > arr[left])
{
return left;
}
else if (arr[midIndex] > arr[right])
{
return midIndex;
}
else
{
return right;
}
}
}
//单趟
int partion(int* arr, int left, int right)
{
assert(arr);
//三数取中,调整基准值
int min = GetMin(arr, left, right);
Swap(&arr[left], &arr[min]);
int key = left;
//当左右还未相撞时
while (left < right)
{
//从右边找到比key小的值,然后等左边找到比key大的值
while (left < right && arr[key] < arr[right])
{
--right;
}
//从左边找到比key大的值
while (left < right && arr[key] > arr[left])
{
++left;
}
//两边都找到后,交换
Swap(&arr[left], &arr[right]);
}
//相遇后,与key位置的值交换
Swap(&arr[key], &arr[left]);
return left;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
assert(arr);
if (left > right)
{
return;
}
int keyIndex = partion(arr, left, right); //key位置的值排好序后的真实下标
//排左边
QuickSort(arr, left, keyIndex - 1);
//排右边
QuickSort(arr, keyIndex + 1, right);
}
挖坑版本
这里对于快速排序要介绍的第二个版本就是挖坑法。
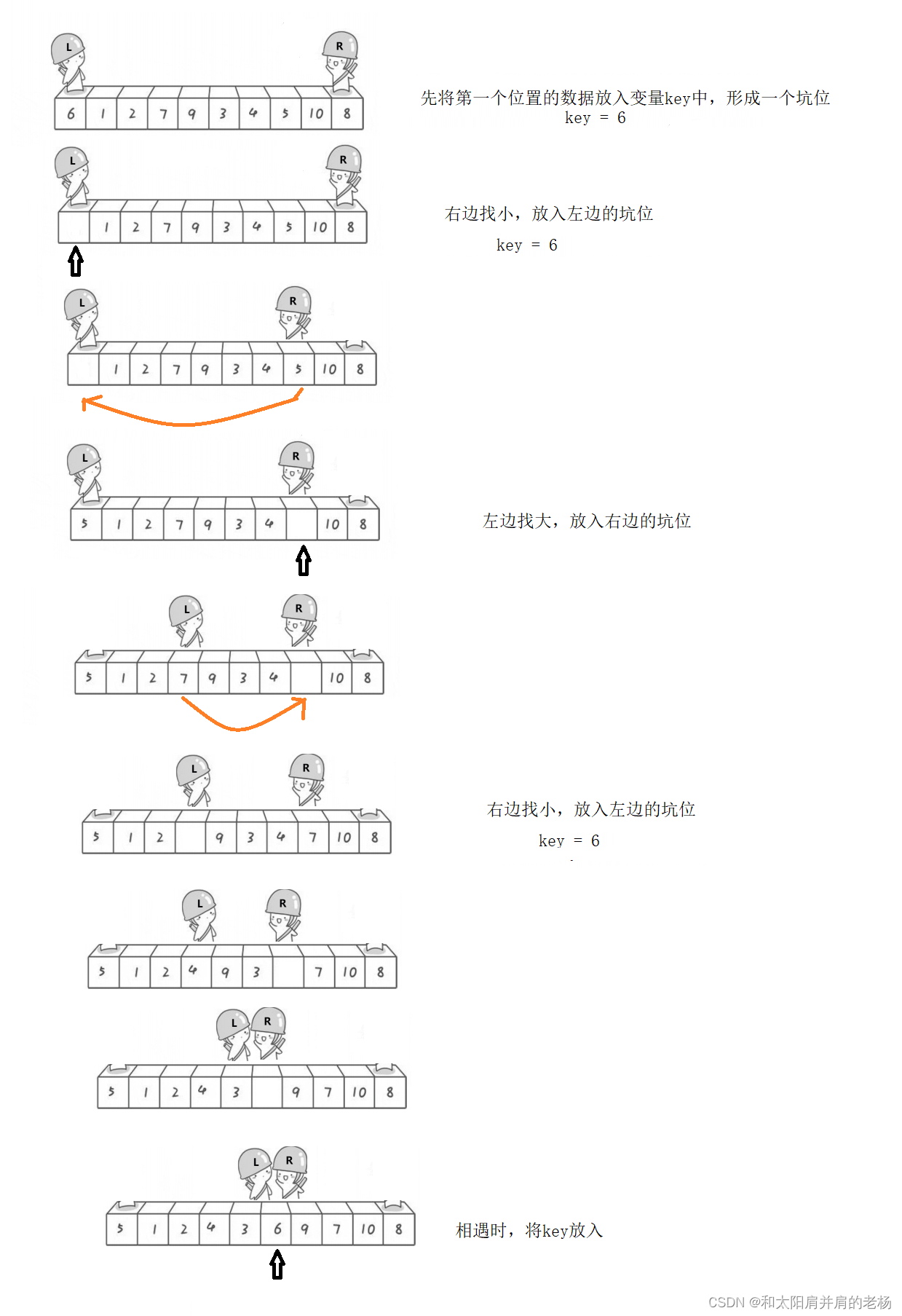
此时keyz左边的子序列均比key小,而右边的序列均比key大,说明我们已经找到key排好序后真实所在的位置。将所有的都找到后,则排序成功
【参考代码】
//单趟,挖坑法
int partion2(int* arr, int left, int right)
{
assert(arr);
//三数取中法,调整
int mid = GetMid(arr, left, right);
Swap(&arr[left], &arr[mid]);
//形成坑位
int pit = left;
int key = arr[left];
while (left < right)
{
//右边找小
while (left < right && arr[right] > key)
{
--right;
}
//放入左边坑位,并且形成新坑位
arr[pit] = arr[right];
pit = right;
//左边找大
while (left < right && key > arr[left])
{
++left;
}
//放入右边坑位,并且形成新坑位
arr[pit] = arr[left];
pit = left;
}
//相遇时,将key放入坑位
arr[pit] = key;
return pit;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
assert(arr);
if (left > right)
{
return;
}
int keyIndex = partion2(arr, left, right); //key位置的值排好序后的真实下标
//排左边
QuickSort(arr, left, keyIndex - 1);
//排右边
QuickSort(arr, keyIndex + 1, right);
}
前后指针版本
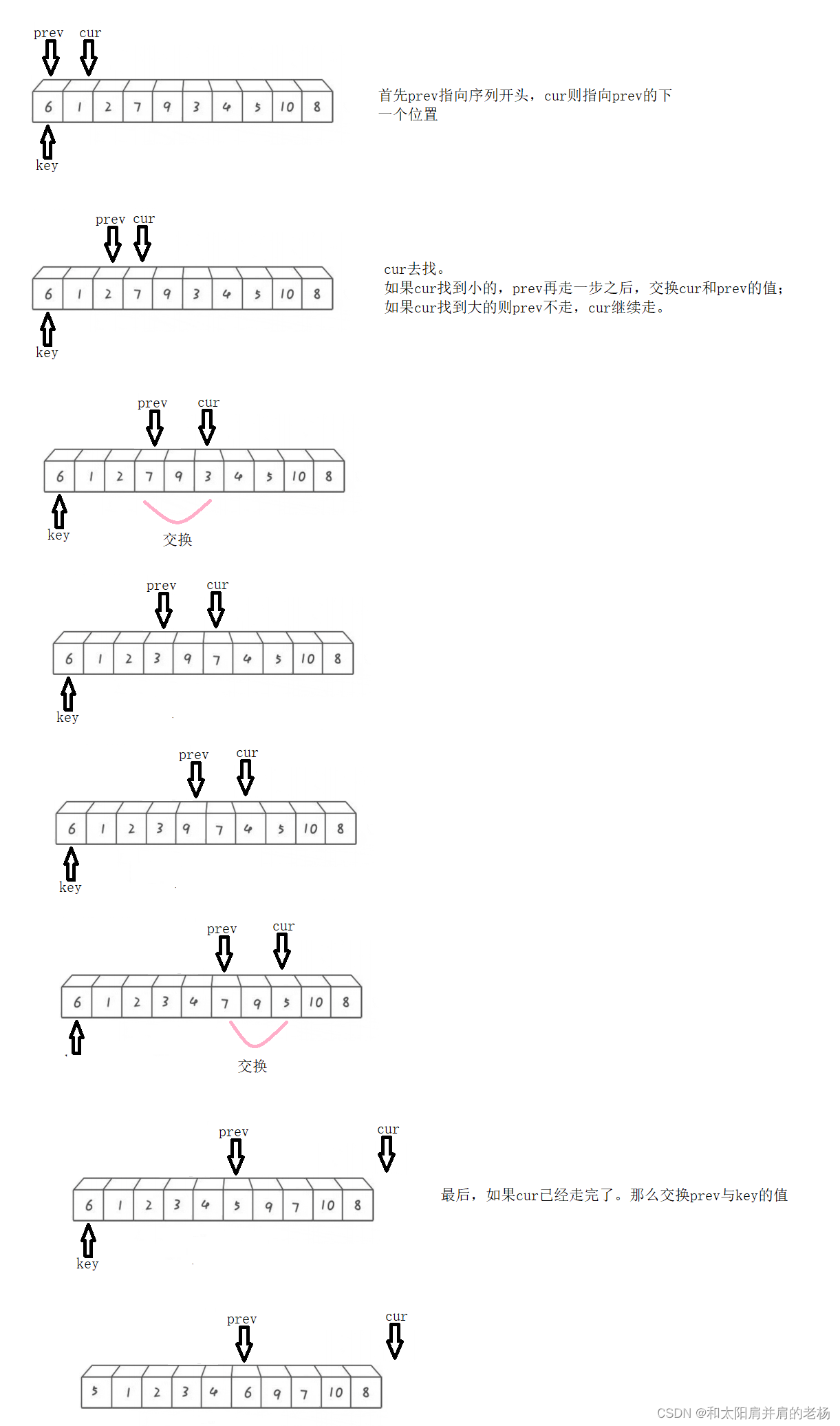
此时key左边的子序列均比key小,而右边的序列均比key大,说明我们已经找到key排好序后真实所在的位置。将所有的都找到后,则排序成功
【参考代码】
//单趟,前后指针版本
int partion3(int* arr, int left, int right)
{
assert(arr);
//三数取中法调整
int mid = GetMid(arr, left, right);
Swap(&arr[left], &arr[mid]);
//首先prev指向序列开头,cur指向prev的下一个
int prev = left;
int cur = left + 1;
int key = left;
while (cur <= right)
{
//如果找到小的则prev再走一步之后交换
if(arr[cur] < arr[key] && ++prev != cur)
{
Swap(&arr[prev], &arr[cur]);
}
++cur;
}
Swap(&arr[left], &arr[prev]);
return prev;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
assert(arr);
if (left > right)
{
return;
}
int keyIndex = partion3(arr, left, right); //key位置的值排好序后的真实下标
//排左边
QuickSort(arr, left, keyIndex - 1);
//排右边
QuickSort(arr, keyIndex + 1, right);
}
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
归并排序
【简述】
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。根据将已有序的子序列合并,得到完全有序的序列的原理;可先使每个子序列有序,再使子序列段间有序,最后在归并成有序序列。若将两个有序表合并成一个有序表,称为二路归并。
这里我就只探讨二路归并。
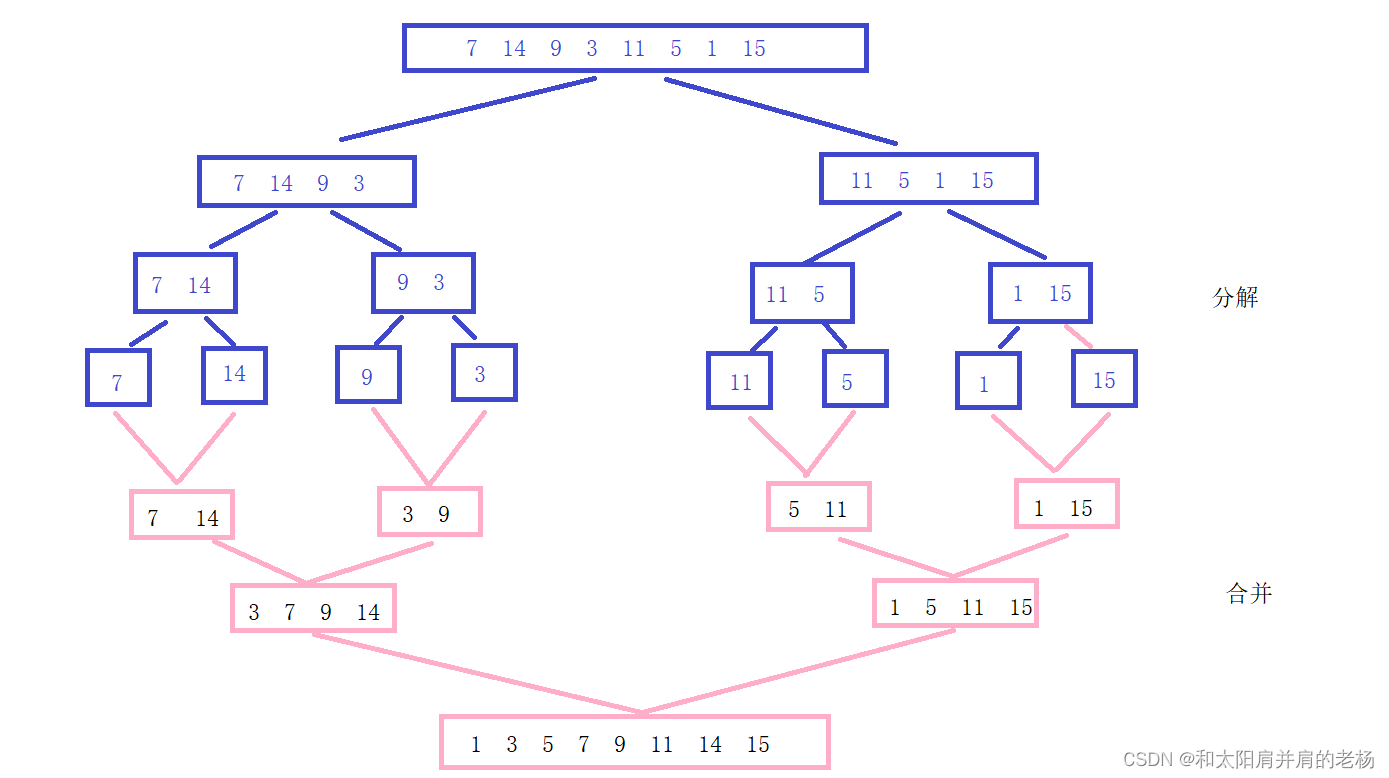
【动图演示】

【参考代码】
void _MergeSort(int* arr, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid + 1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int j = left;
while (begin1 < end1 && begin2 < end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[j++] = arr[begin1++];
}
else
{
tmp[j++] = arr[begin2];
}
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2];
}
//tmp中的数据拷贝回原数组
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
//归并排序
void MergeSort(int* arr, int n)
{
assert(arr);
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail!\n");
exit(-1);
}
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定