[数据结构与算法]2021第十二届蓝桥杯python组真题复盘

从1开始计数，那肯定是1用的最快了，所以算1的个数就好了

num = 0
for i in range(1,10000):
    num += str(i).count('1')
    if num == 2021:
        print(i)
        break
# 3181

从斜率和截距出发确定直线

"""
k = (y1-y2)/(x1-x2)
b = y1-k*x1 = (x1y2 - x2y1)/(x1-x2)
"""

src = [[x, y] for x in range(20) for y in range(21)]
tls = []
num = 0
for i in src:
    x1 = i[0]
    y1 = i[1]
    for j in src:
        x2 = j[0]
        y2 = j[1]
        if x1 == x2:    # 垂直时，斜率为无穷，有x条，最后输出记得加上去
            break
        else:
            k = (y1 - y2) / (x1 - x2)
            b = (x1 * y2 - x2 * y1) / (x1 - x2)
        if [k, b] not in tls:
            tls.append([k, b])
            num += 1
print(num+20)

# 40257

预处理找出能被n整除的数，再在里面找满足乘积为n的数

n = 2021041820210418
src = []
num = 0
tls = []
for i in range(1, int(n ** 0.5) + 1):
    if n % i == 0:
        src.append(i)
        src.append(n // i)
# print(src)
for a in src:
    for b in src:
        for c in src:
            if a*b*c == n and [a,b,c] not in tls:
                num += 1
                tls.append([a,b,c])
print(num)

# 2430

路径长度递增

import math

n = int(input())
dp = [float('inf')] * (n + 1)
dp[1] = 0
for i in range(1, n + 1):
    for j in range(i + 1, i + 22):
        if j > n:
            break
        dp[j] = min(dp[j], dp[i] + (i * j) // math.gcd(i , j))

print(dp[n])

# 10266837

只是时间戳的话可以偷个懒

import time
n = 46800999
new = time.asctime(time.gmtime(n//1000))[11:19]
print(new)

# 13:00:00

杨辉三角每一行是上一行前后加0位后的和

举几个例子

 	`0121`
+ 	`1210`
	`1331`

	`01331`
+	`13310`
	`14641`

	`014641`
+	`146410`
	`15101051`

思路就是检测每一行，出现目标数就返回下标然后结束

n = int(input())

def find_num(n):
    if n == 1:
        return 1
    num = 3
    lit = [1,1]
    while True:
        x = []
        for i in zip([0]+lit,lit+[0]):
            x.append(sum(i))
        lit = x
        if n in lit:
            num += lit.index(n)+1
            break
        else:
            num += len(lit)
    return num

print(find_num(n))

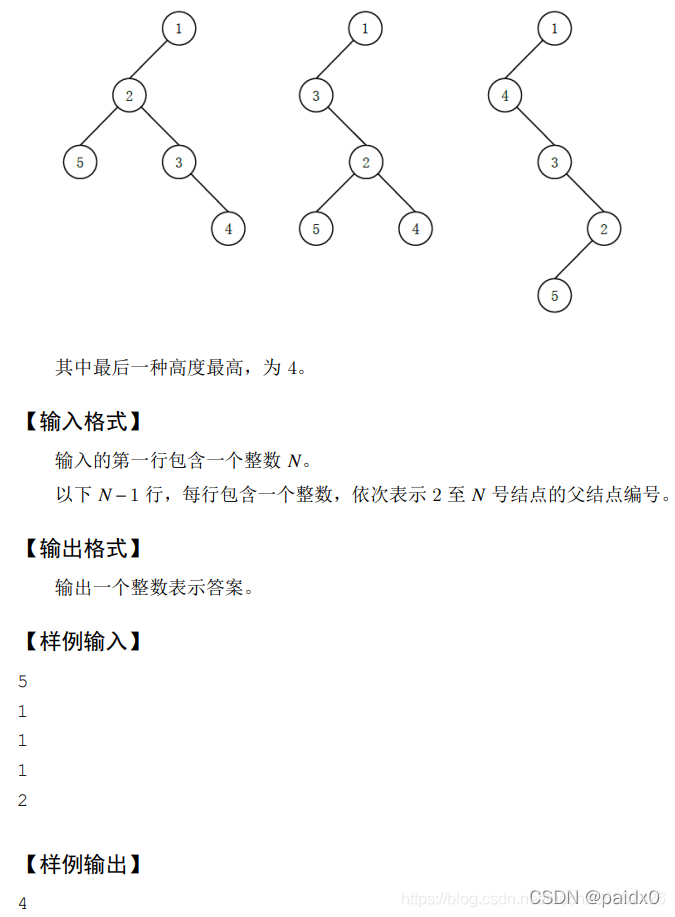
时间超限76，但还是记录一下吧

def dfs(x):
    ret = 1;
    for i in range(len(u[x])):
        temp = dfs(u[x][i]) + len(u[x])
        ret = max(temp, ret)
    return ret

n = int(input())
u = [[] for _ in range(n+1)]
for i in range(n-1):
    u[int(input())].append(i+2)
print(dfs(1)-1)