



题意:

思路:
本题是一道 01背包 的扩展题 —— 二维费用01背包问题,其本质和经典01背包没有区别
把 野生小精灵 看做 物品,则将捕捉需要的 精灵球个数 定为 第一费用,皮卡丘要消耗的体力 定为 第二费用
最后答案要求物品数量最多,因此我们可以用状态的属性来表示选择的物品数
以上就是本题的 阅读理解 分析部分 ,接下来上 闫氏DP分析法:
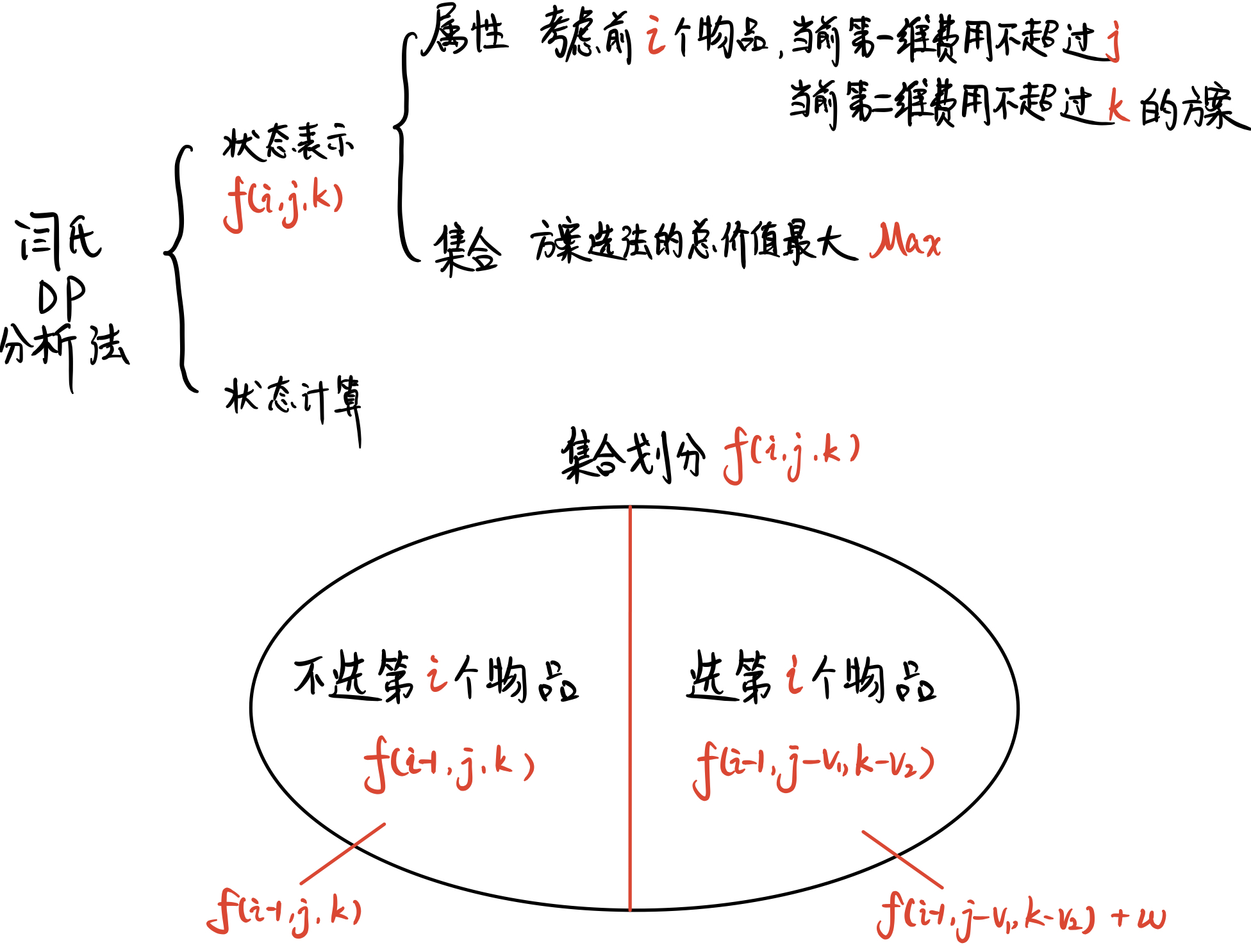
上图展示的是三维朴素,我们用代码实现的时候将省去第一维(野生小精灵数量),类比最经典的01背包问题
注意,题目提到:
-
①使得皮卡丘体力小于等于
0的野生小精灵也不会被小智收服,因此皮卡丘的体力值需在m - 1时开始 -
②如果可以收服的小精灵数量一样,小智希望皮卡丘受到的伤害越小(剩余体力越大),因此在最后还需要从小到大遍历
f[n][i](i = 0,1,...,m-1),当初次与f[n][m-1]相等时即受到的伤害最小,即剩皮卡丘余体力最大
时间复杂度:
O(KNM)
代码:
#include<bits/stdc++.h>
using namespace std;
int n, m, k;
const int N = 1010, M = 510;
int dp[N][M];
int main()
{
cin>>n>>m>>k;//精灵球数量、皮卡丘初始的体力值、野生小精灵的数量
for(int i=1;i<=k;++i)
{
int v1, v2;
cin>>v1>>v2;
//j,k二维费用,分别为 消耗精灵球数 和 皮卡丘消耗体力数
for(int j=n;j>=v1;--j)
for(int l=m-1;l>=v2;--l)//皮卡丘的体力值需在m - 1时开始,原因如上
dp[j][l] = max(dp[j][l], dp[j-v1][l-v2]+1);
}
cout<<dp[n][m-1]<<' ';
int ans = 0;
//从小到大循环精灵对皮卡丘造成的伤害
for(int i=0;i<=m-1;++i) if(dp[n][i]==dp[n][m-1]) {ans = i; break;}
cout<<m-ans<<endl;//跳出循环时ans为最小伤害值,m-ans即为皮卡丘的剩余体力值的最大值
return 0;
}