[数据结构与算法]（校赛）救救曹植（贪心）

题目链接：OnlineJudge

题目：

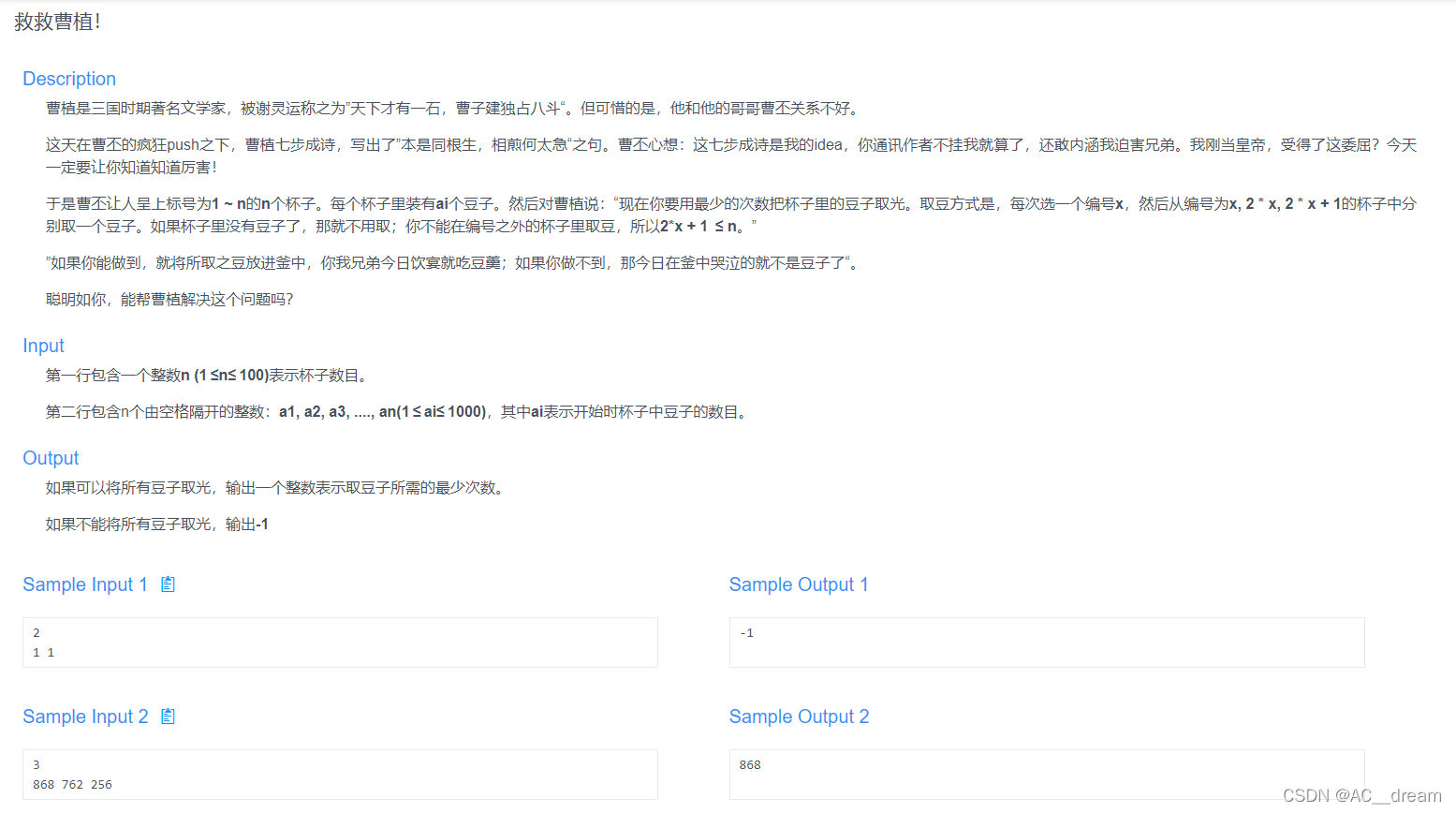
分析：这道题目是倒序贪心，我们先来思考一个问题，假如n为偶数，那么能不能把所有的豆子都取光呢？显然是不能的，因为无论我们取x为几，第n个杯子的豆子都取不到，因为n+1超过了边界，所以这种情况可以特判掉，还有什么情况也是取不光的呢？就是只有一个杯子的时候，为什么这个时候杯子里面的豆子是取不光的呢？因为只有一个杯子，所以我们只能选择x=1，但是这个时候2*x+1=3超出了边界，所以x=1也不能选，所以这种情况也是取不光的，除了这两种情况之外其他情况都是能取光的，我们下面来进行分析：

对于任意的k<=n：

如果k是偶数，我们可以令x=k/2，而且由于n是奇数，所以k+1<=n，所以这个时候是能取光的

如果k是奇数，我们可以令x=(k-1)/2，这个时候也能将豆子取光

而我们的贪心策略正是上述分析的那样：

假如我们当前取到了第k个杯子，则编号在k+1~n的杯子都已经被取光，那我们应该取编号为几的杯子呢？其实应该是(k-1)/2，换句话说，只能是编号为(n-1)/2的杯子，因为当编号大于(k-1)/2时乘以2加1后是大于k的，而编号小于(k-1)/2的杯子乘以2加1后是小于k的，所以第k个杯子必须由第(n-1)/2个杯子取完。而假如我们当前取到了第k个杯子，则编号在k+1~n的杯子都已经被取光，刚才我们讨论了k为奇数的情况，下面我们来讨论一下k为偶数的情况，同理，k也只能被编号为k/2的杯子取光，分析方式也是一样的，因为从分析中我们可以发现，我们利用这个思路所作出的每一步决策都是必要的，所以利用这个思路我们得到的就是最优解。

下面是代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=103;
int a[N];
int main()
{
	int ans=0;
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	if(n==1||n%2==0)
	{
		puts("-1");
		return 0;
	}
	for(int i=n;i>=1;i--)
	{
		if(a[i]>0)
		{
			if(i&1)
			{
				ans+=a[i];
				a[i-1]-=a[i];
				a[i/2]-=a[i];
			}
			else
			{
				ans+=a[i];
				a[i/2]-=a[i];
			}
		}
	}
	printf("%d",ans);
	return 0;
}