图基础
图的定义
图G由顶点集V和边集E组成,记为G = (V,E),其中V(G)表示图G中顶点的有限非空集;E(G)表示图G中顶点之间的关系(边)集合。若V = {v1,v2,…,vn},则用|V|表示图G中顶点的个数,也称为图G的阶,E = {{u,v} | u∈V,v∈V},用|E|表示图G中边的条数
注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
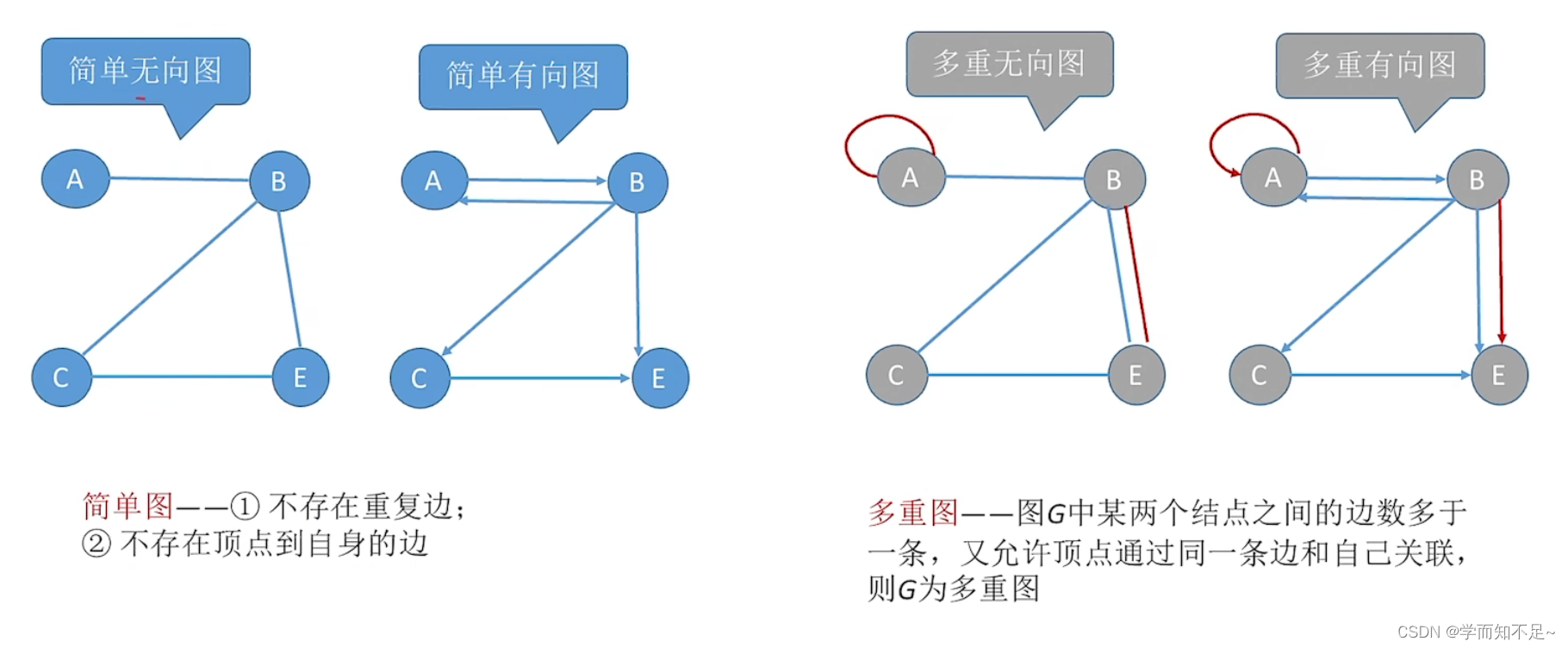
无向图、有向图
若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v,w)或(w,v),因为(v,w)=(w,v),其中v、w是顶点。可以说顶点w和顶点v互为邻接点,边(v,w)依附于顶点w和v,或者说边(v,w)和顶点v、w相关联
若E是有向边(也称弧)的有限集合时,则图G为有向图。弧是顶点的有序对,记为<v,w>,其中v、w是顶点,v称为弧尾,w称为弧头。<v,w>称为从顶点v到顶点w的弧,也称v邻接到w,或w邻接自v。<v,w> != <w,v>
简单图、多重图
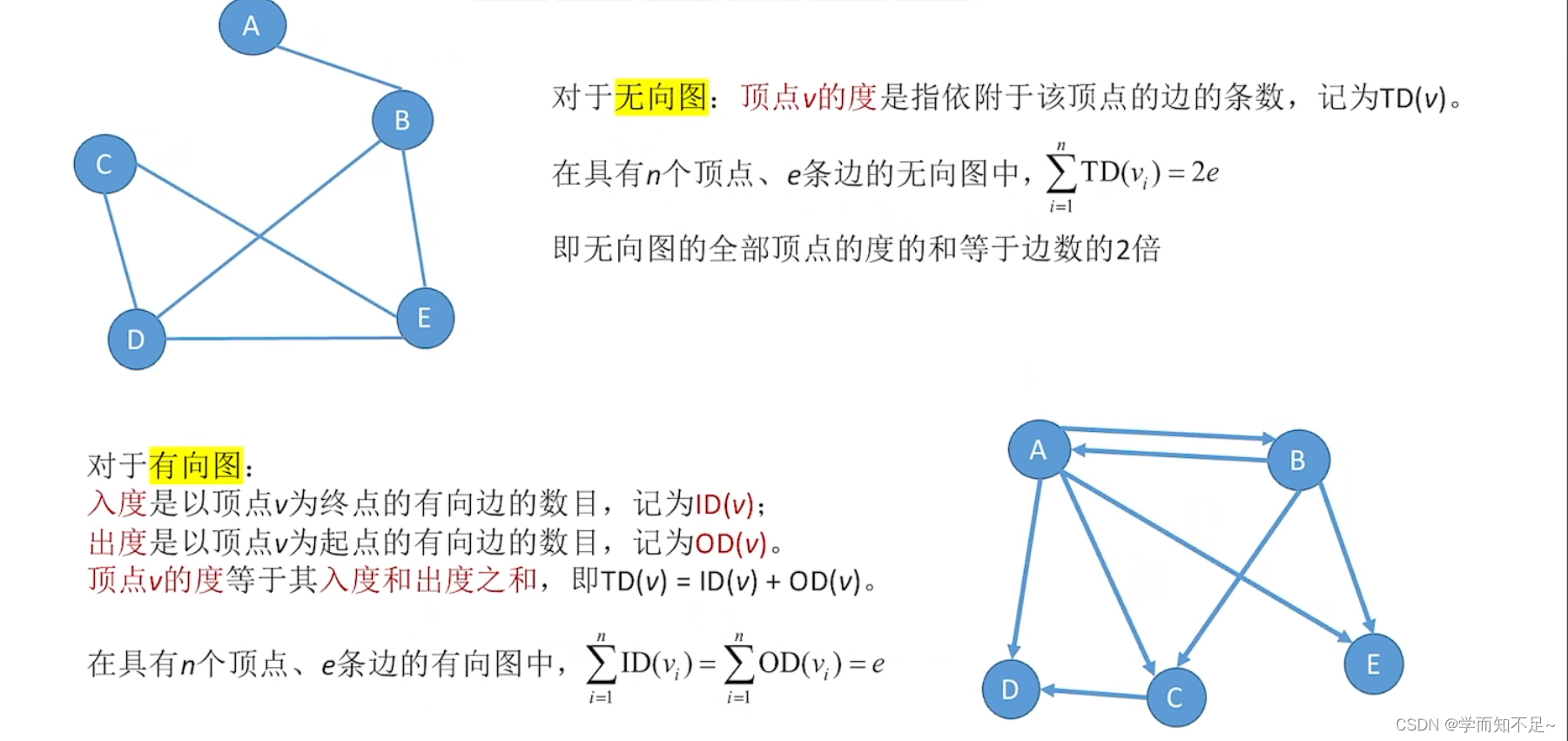
顶点的度、入度、出度
顶点-顶点的关系描述

连通图、强连通图
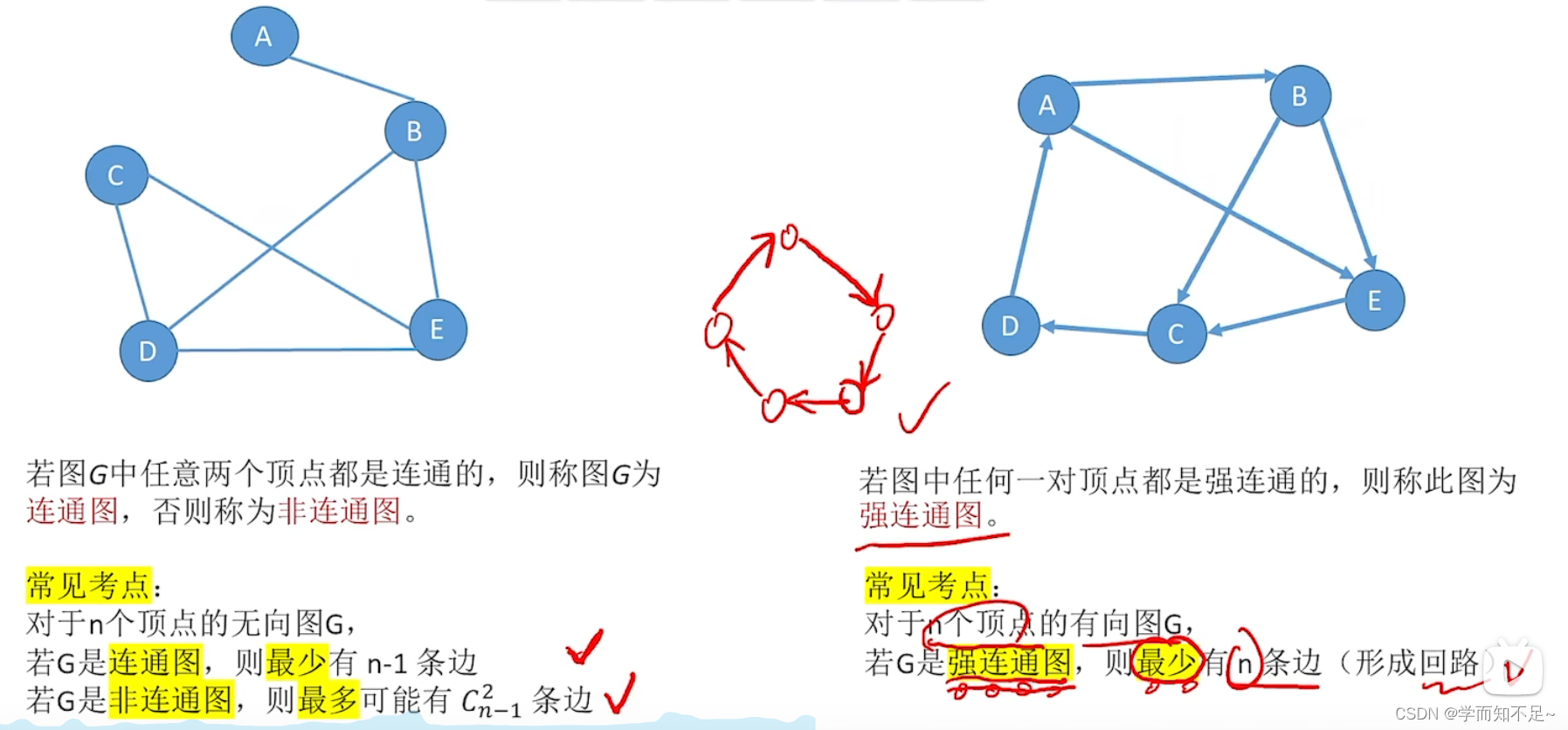
连通图最少有n-1条边是因为n个节点两两相连
非连通图最多有的情况是当其他n-1个节点两两相连,而最后一个节点一个都不连
子图
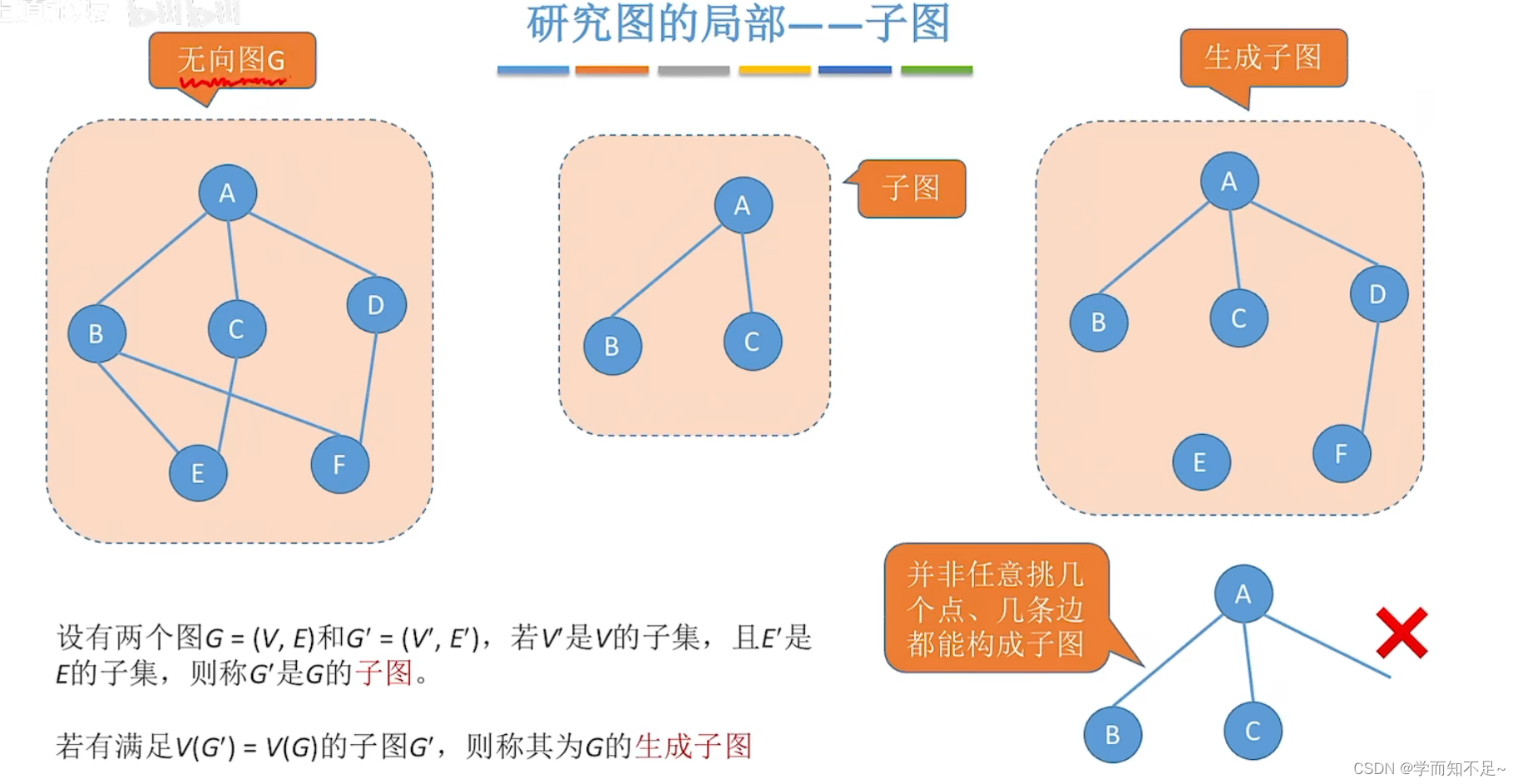
生成子图是拥有原图所有点的子图
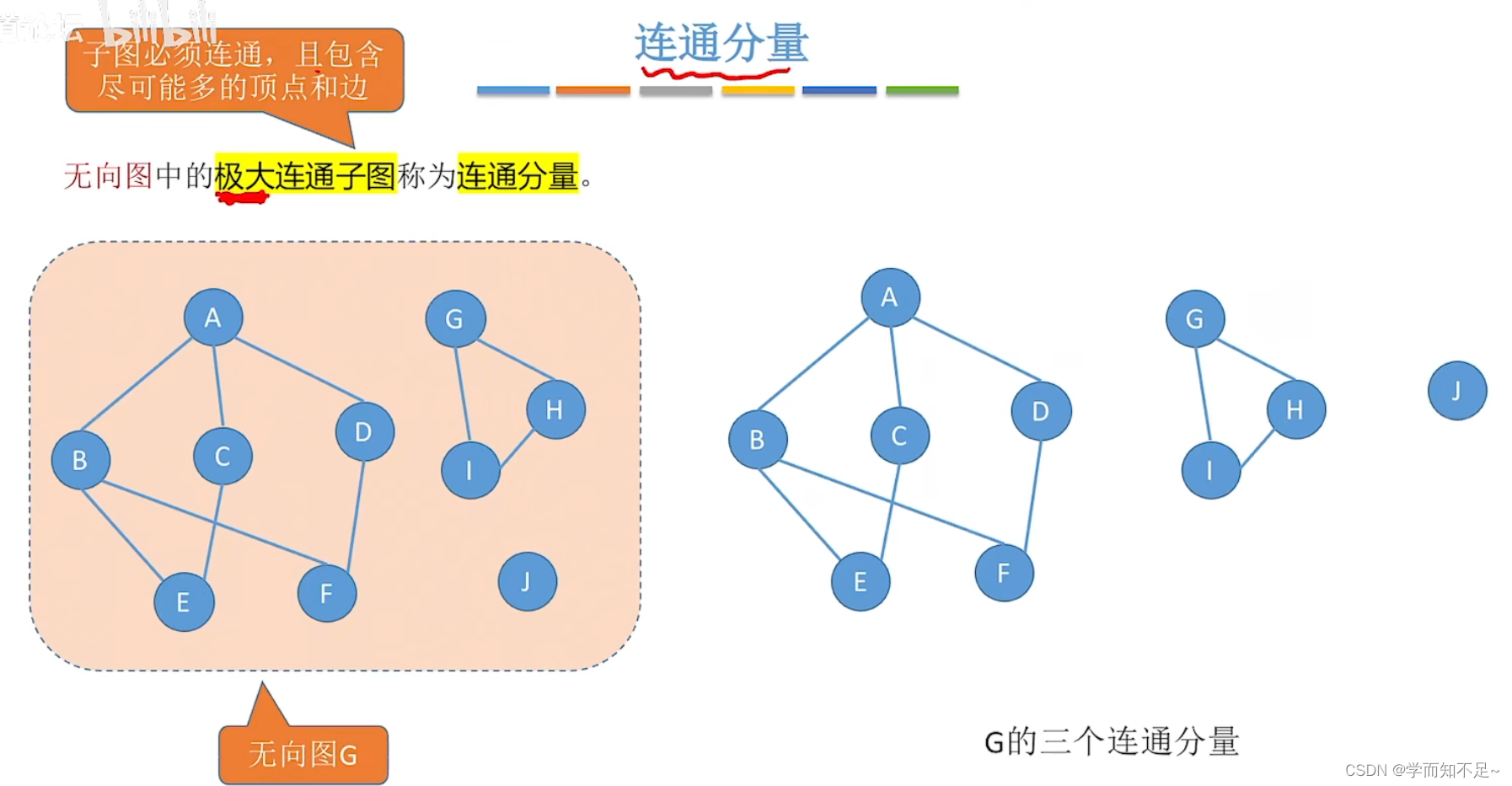
连通分量
用于描述无向图
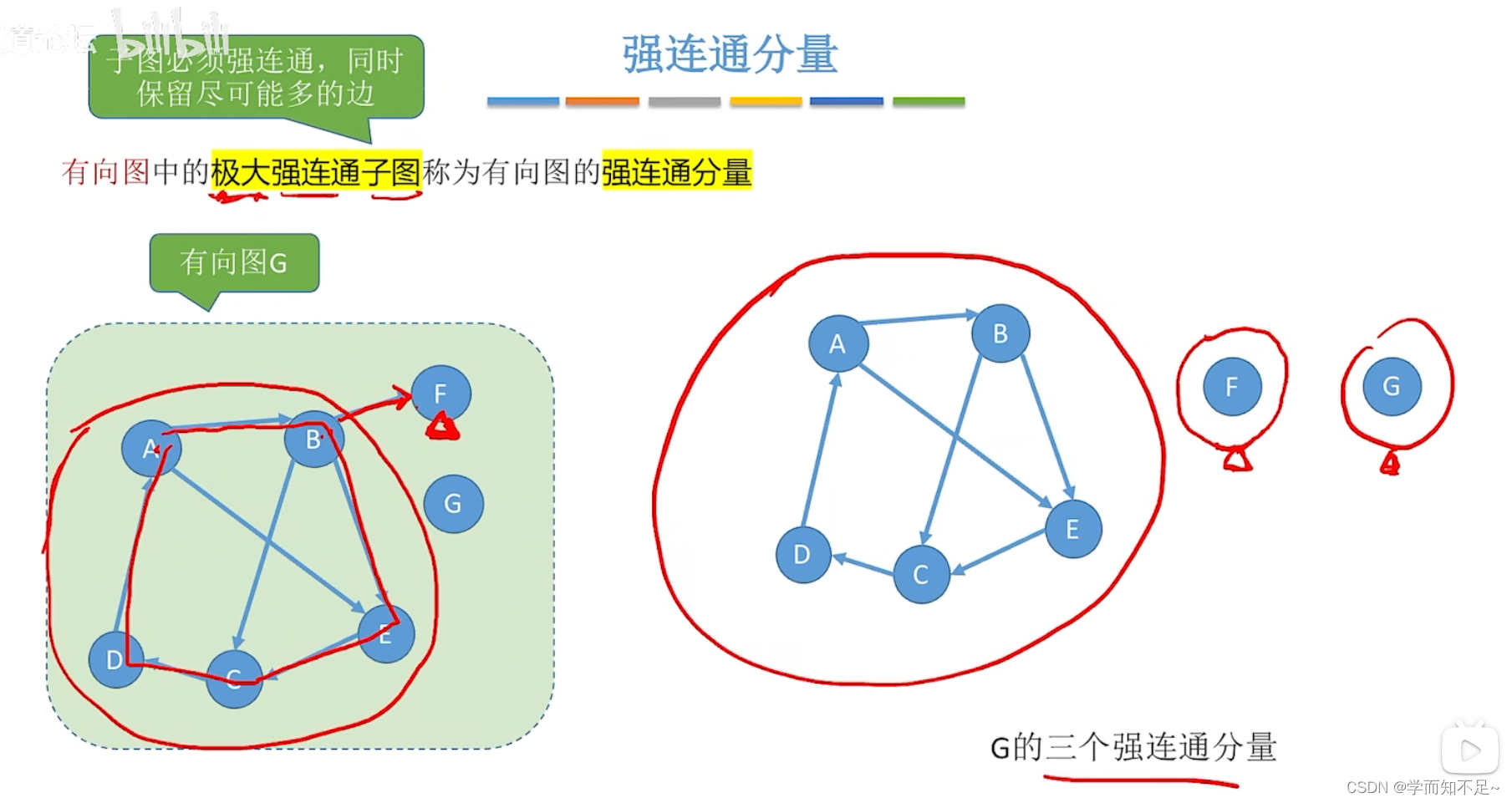
强连通分量
用于描述有向图
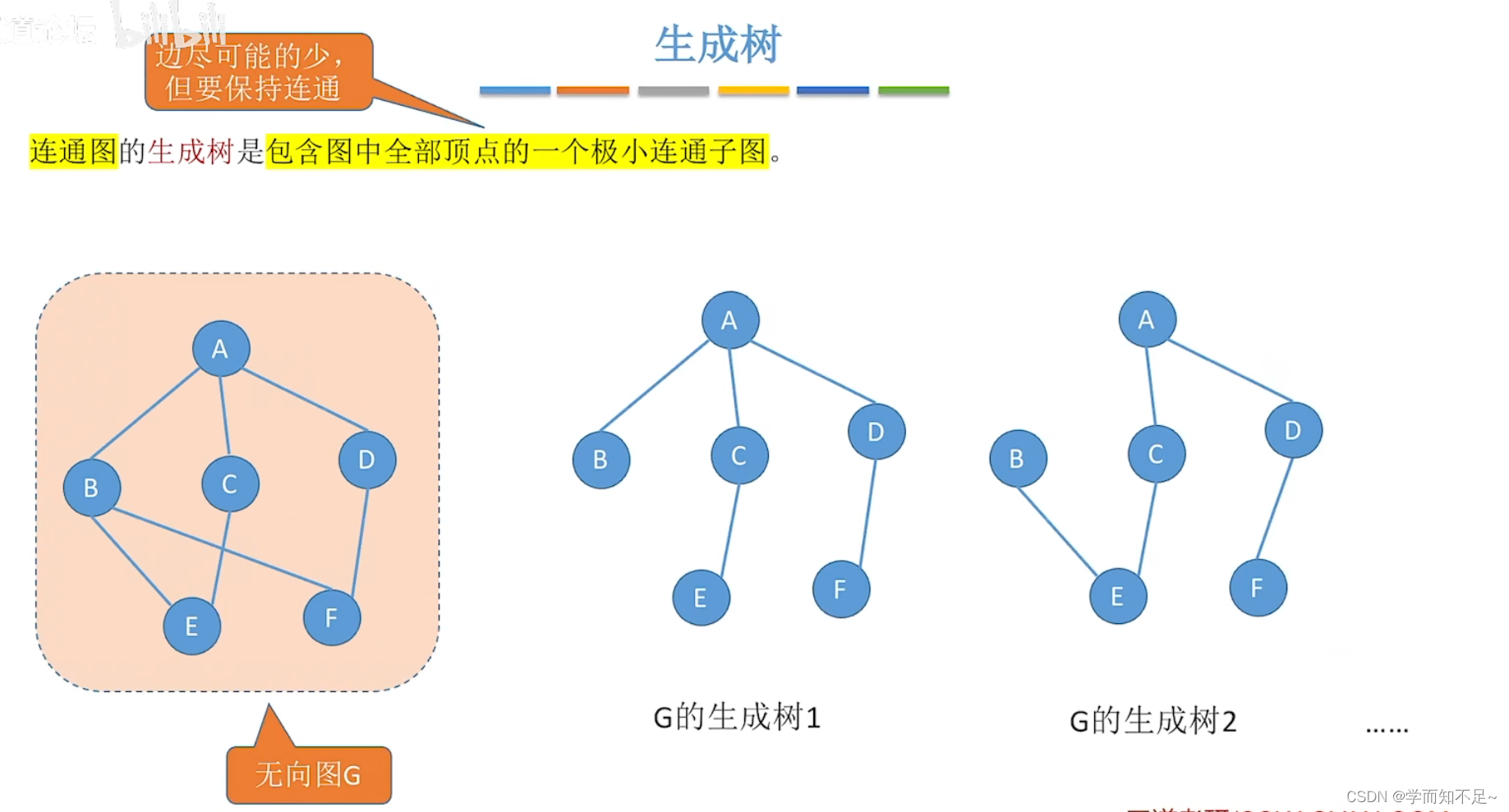
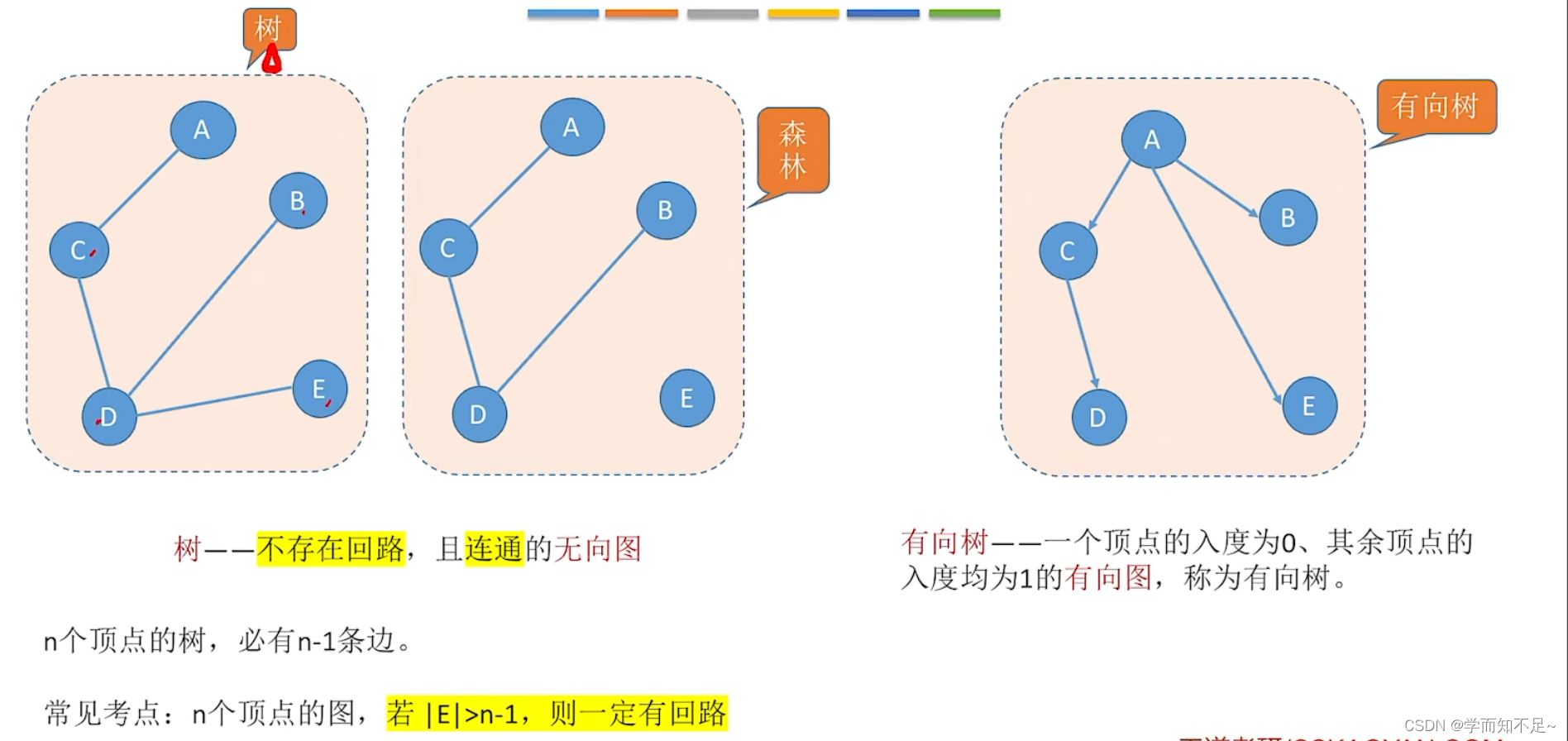
生成树
n个顶点有n-1条边,再多就会形成回路
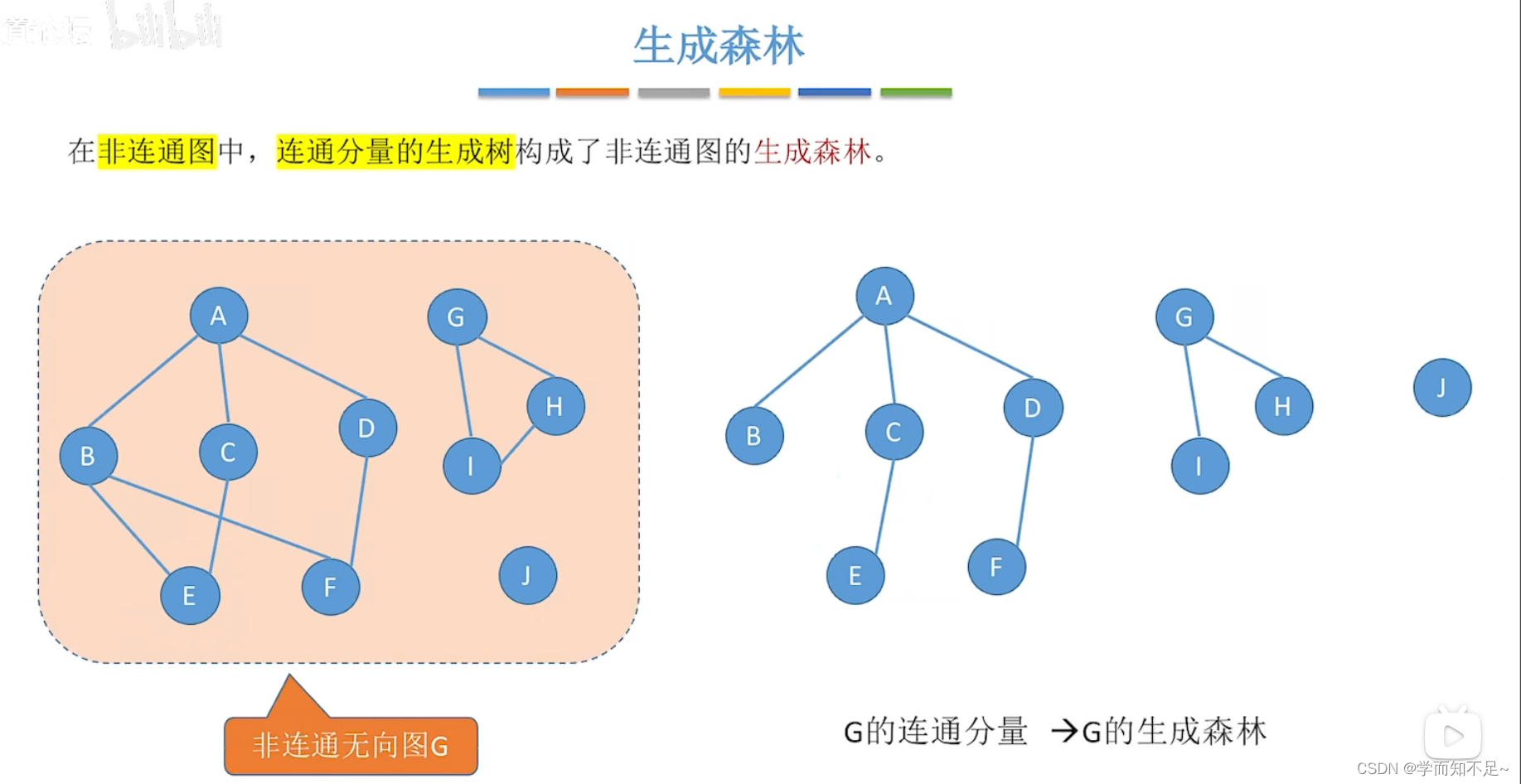
生成森林
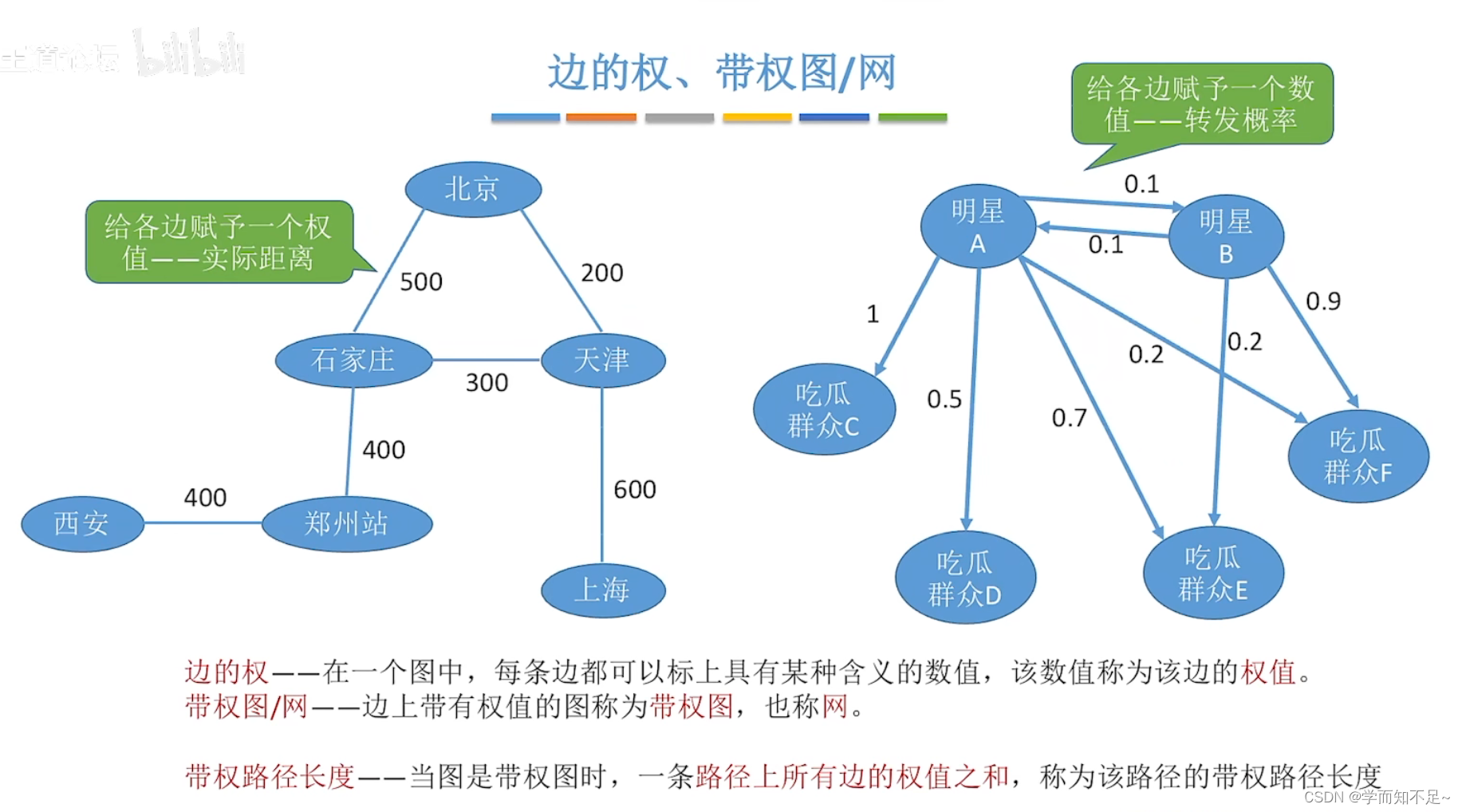
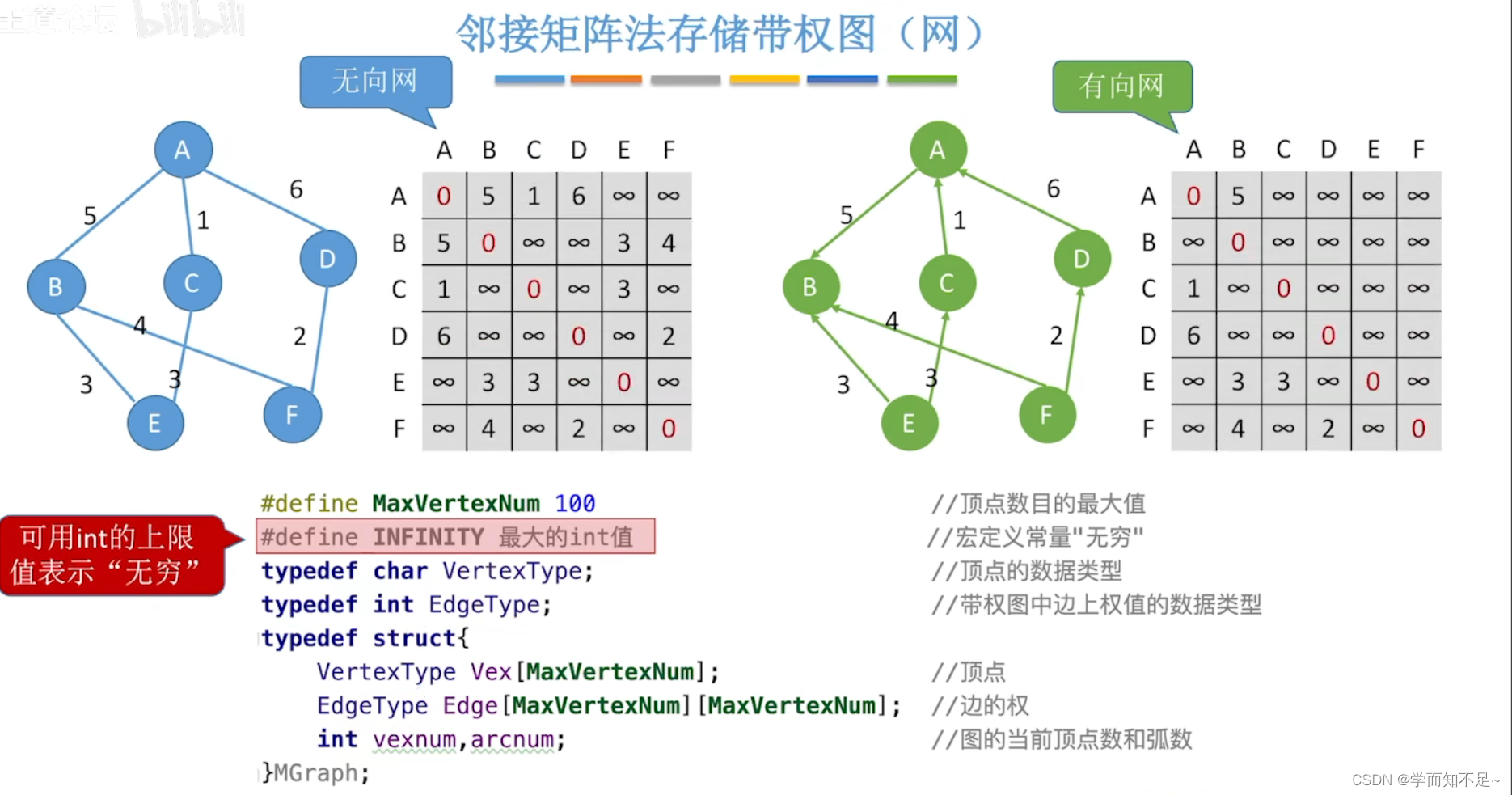
边的权、带权图/网
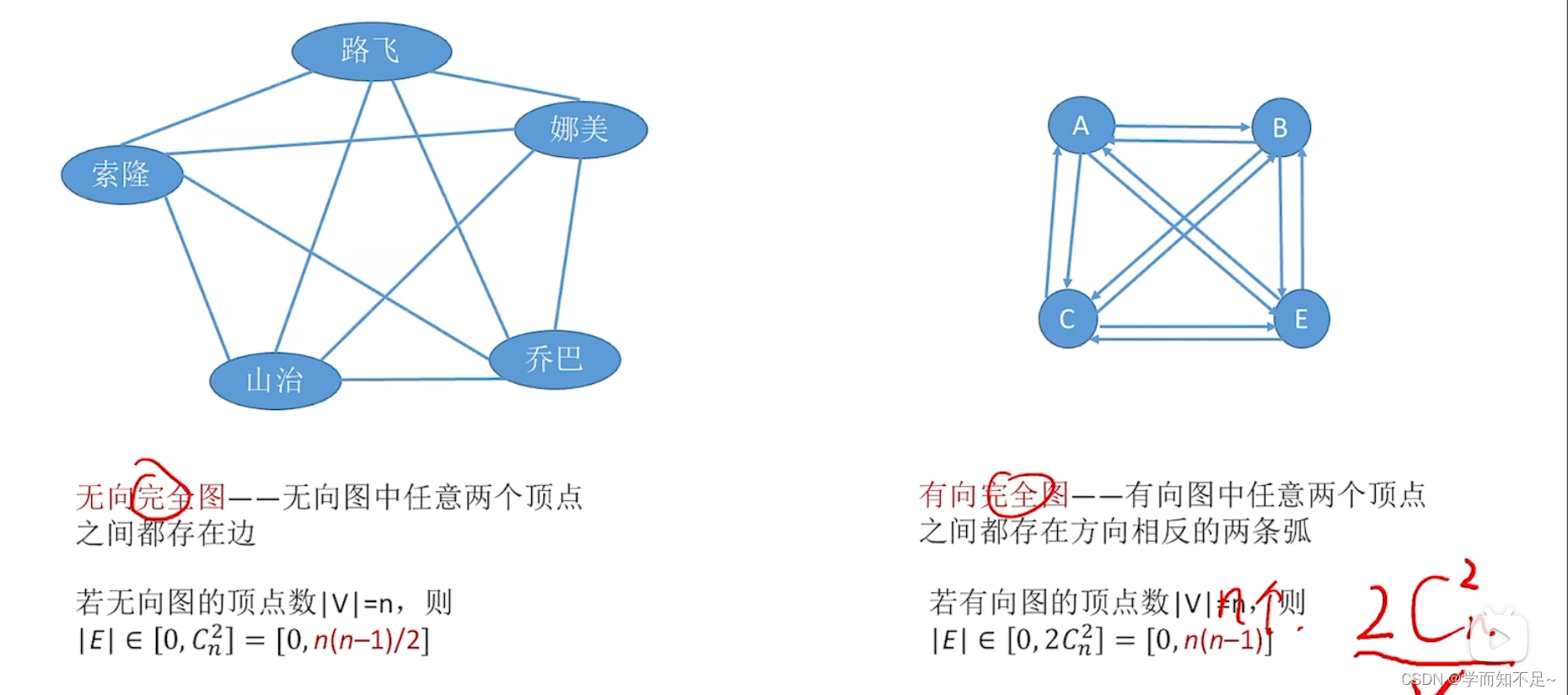
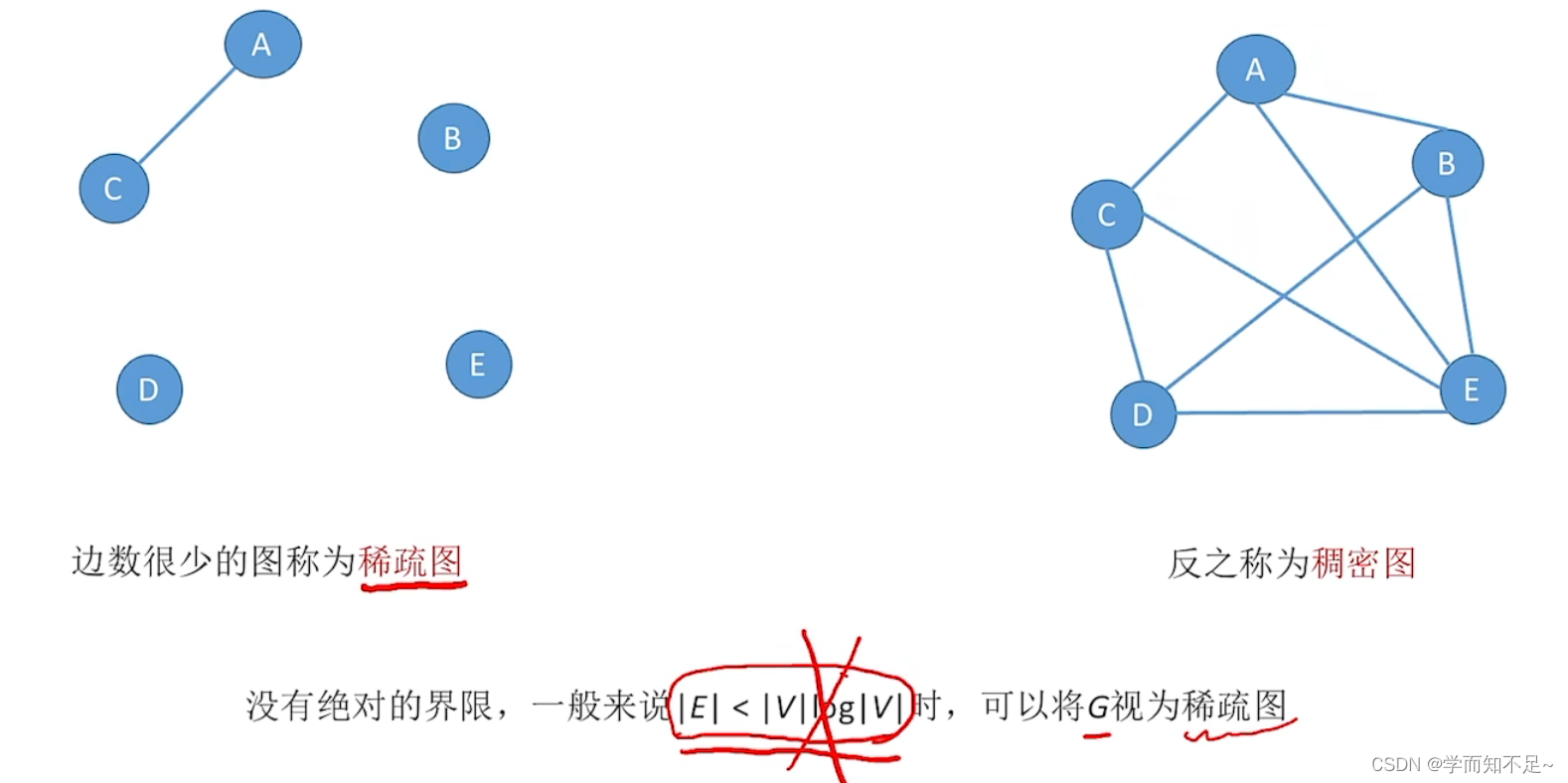
几种特殊形态的图
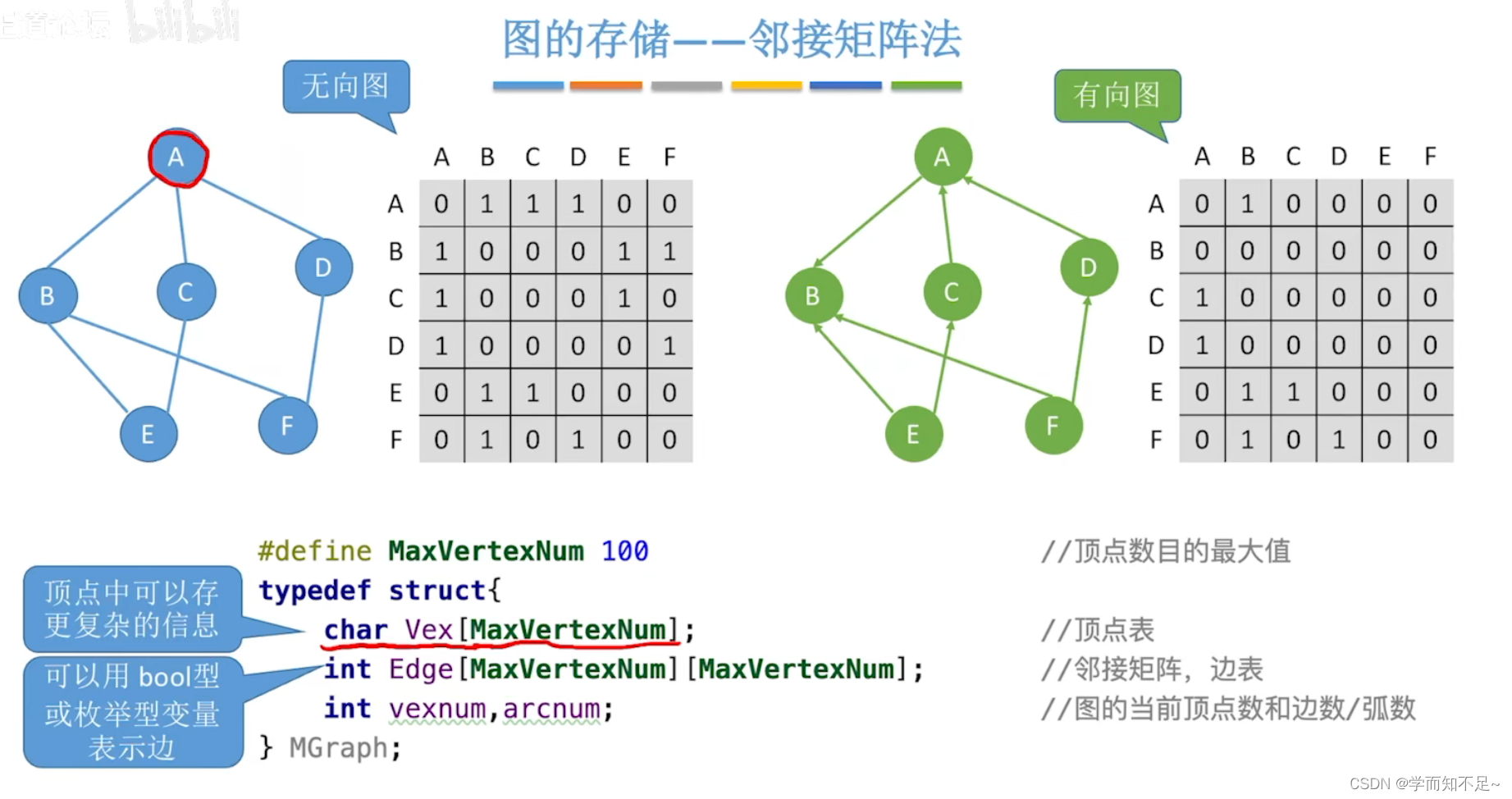
图的存储结构
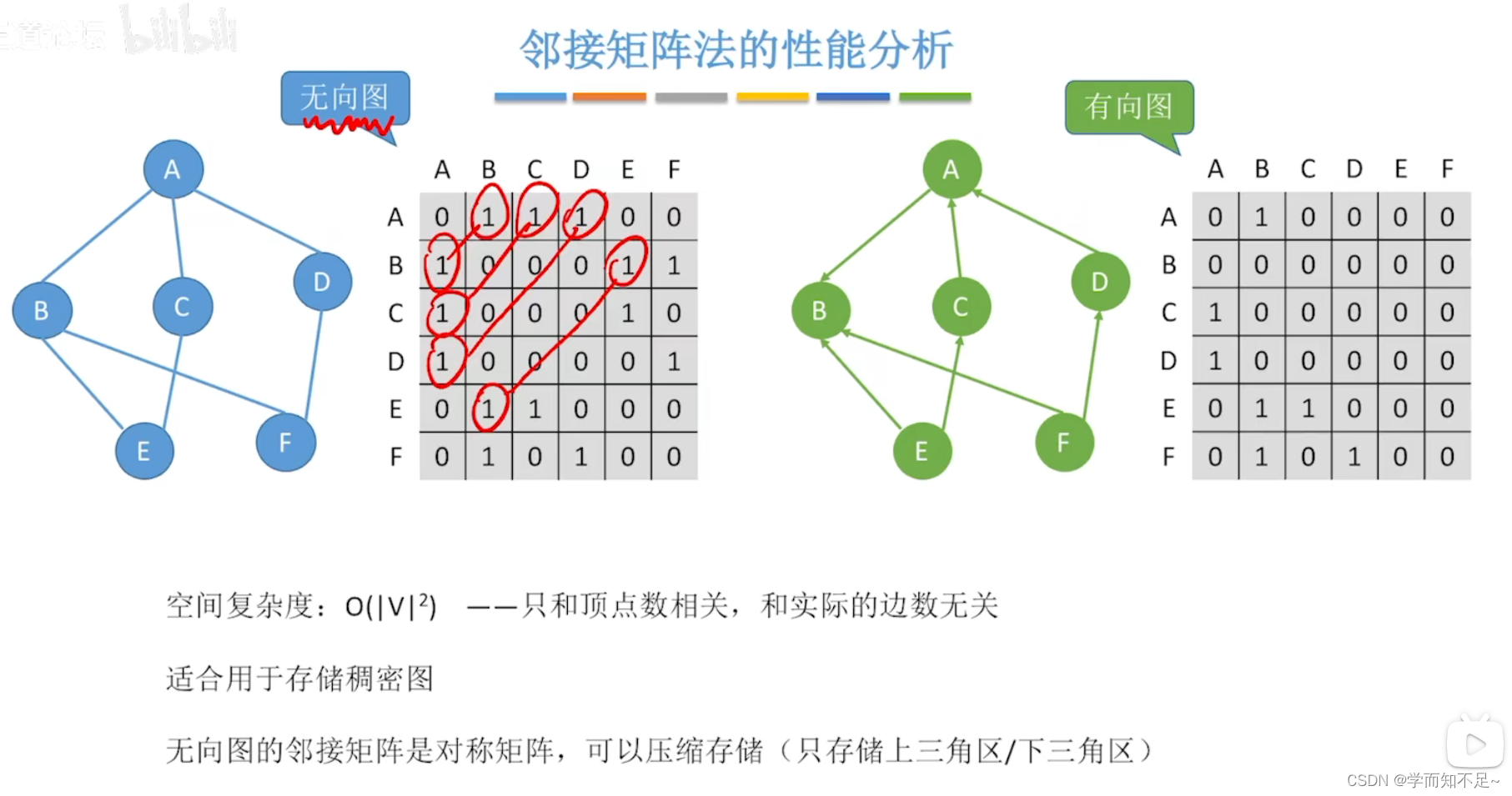
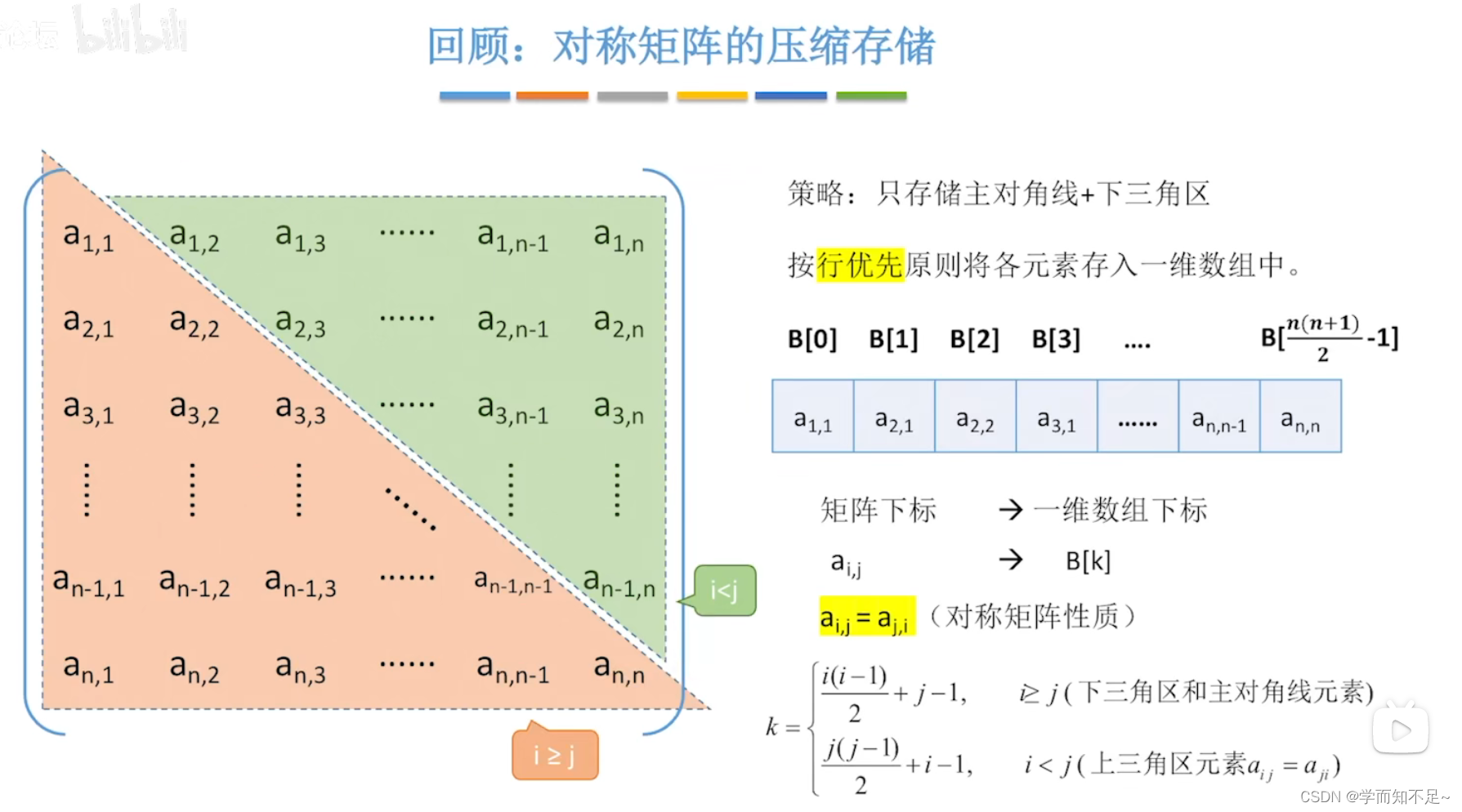
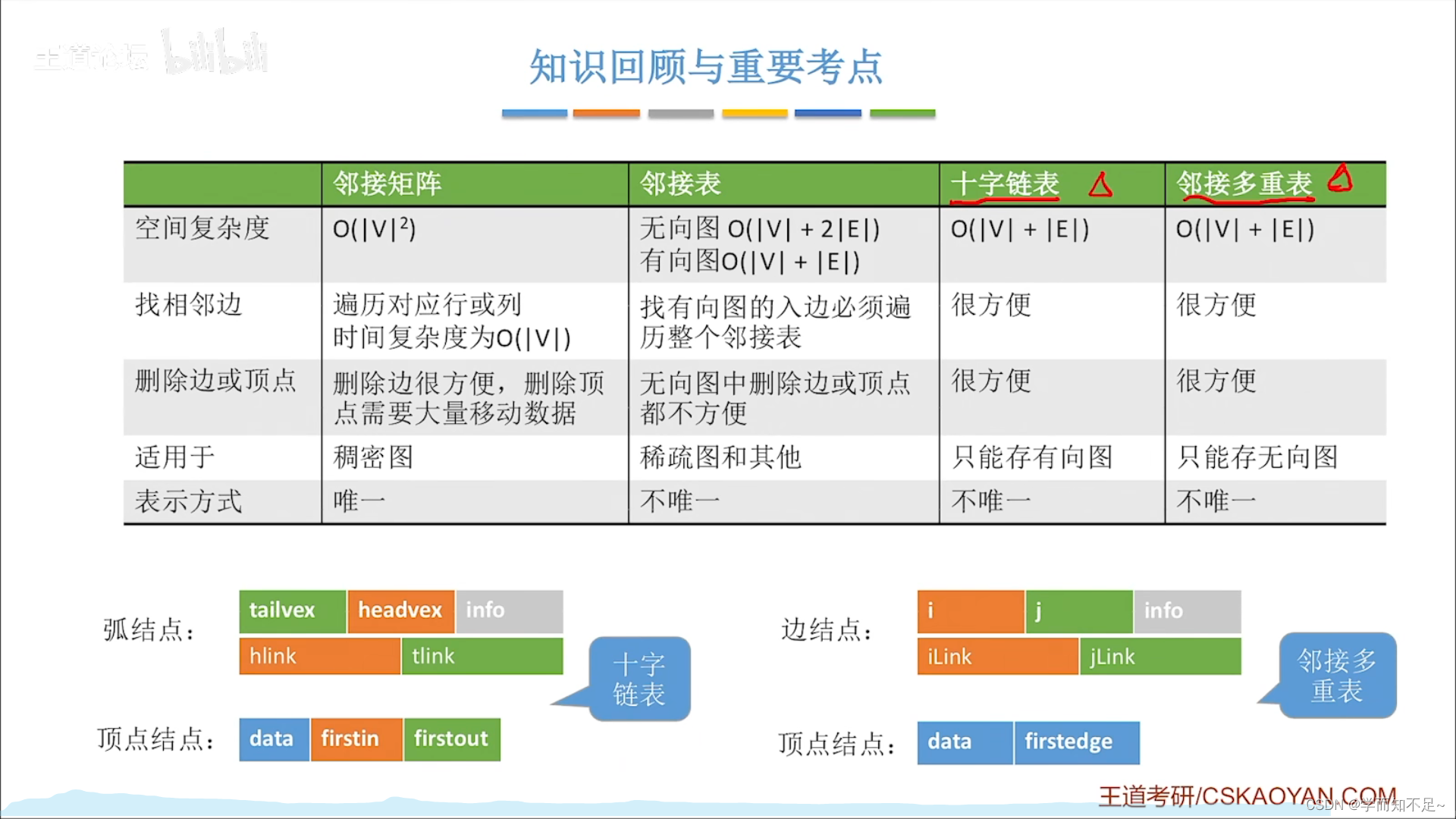
- 邻接矩阵:数组实现的顺序存储,空间复杂度高O(n2),不适合存储稀疏图
- 邻接表:找有向图的入度不方便,删除顶点、删除边的时间复杂度高
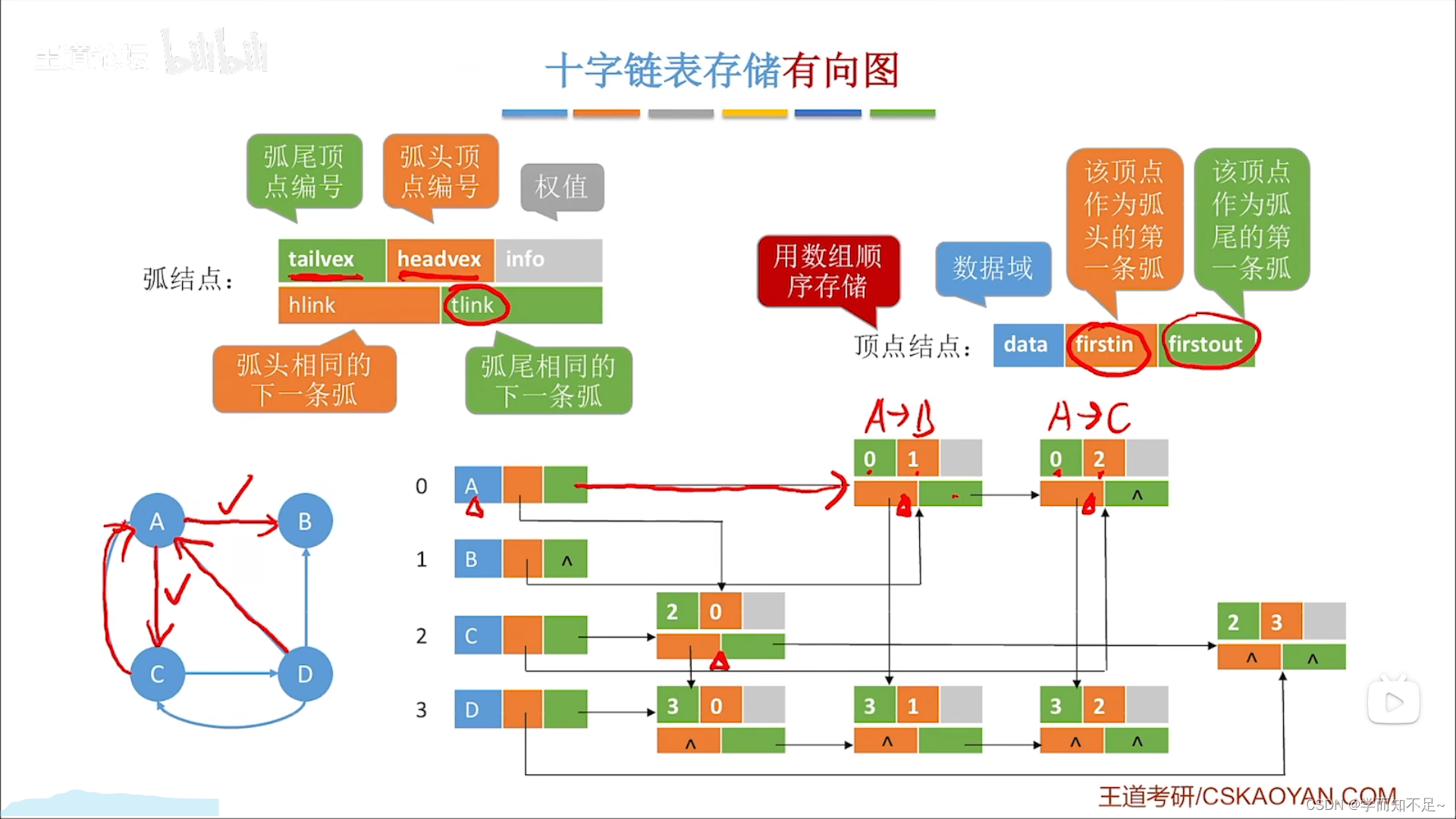
- 十字链表:存储有向图
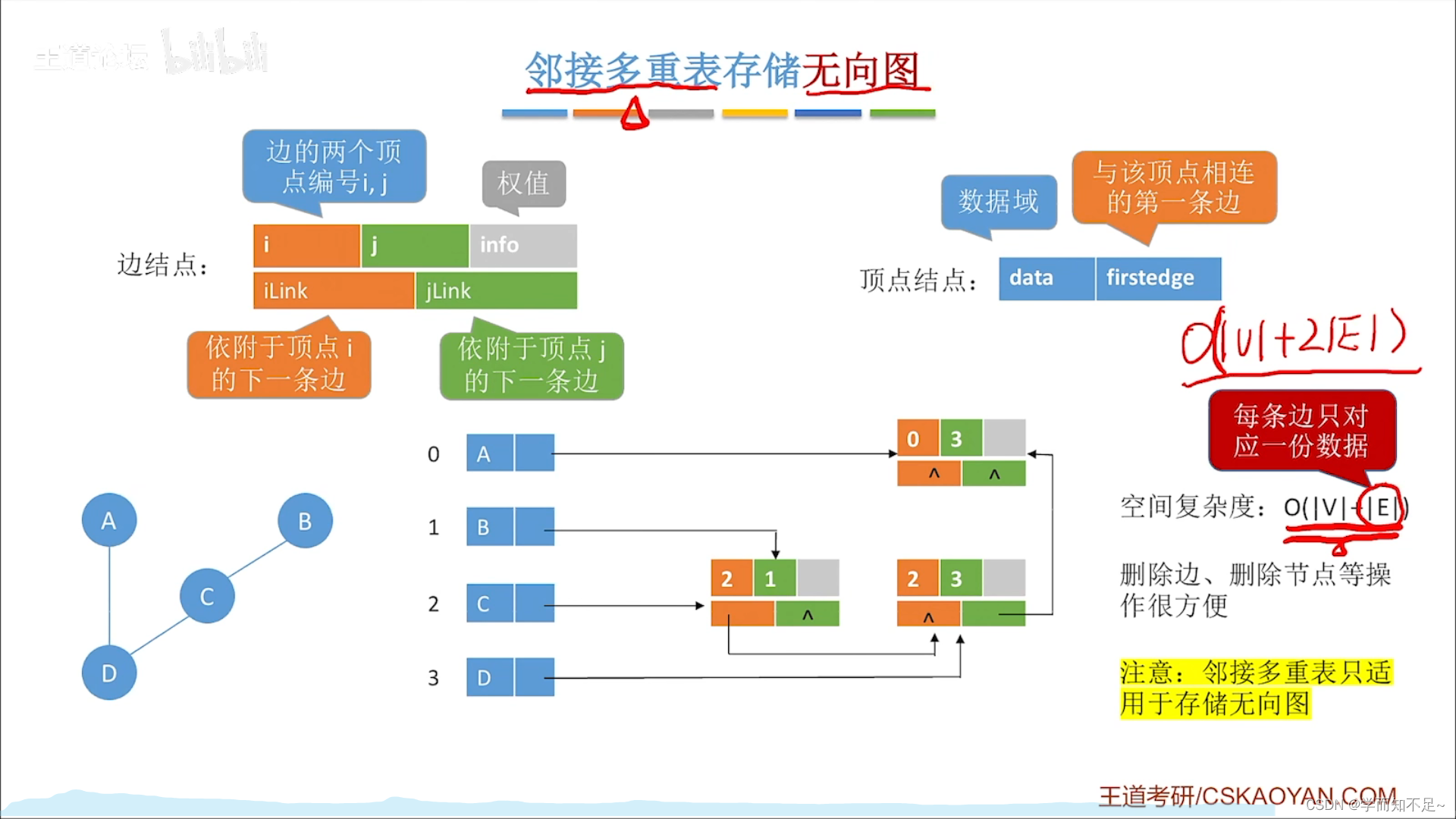
- 邻接多重表:存储无向图
邻接矩阵法

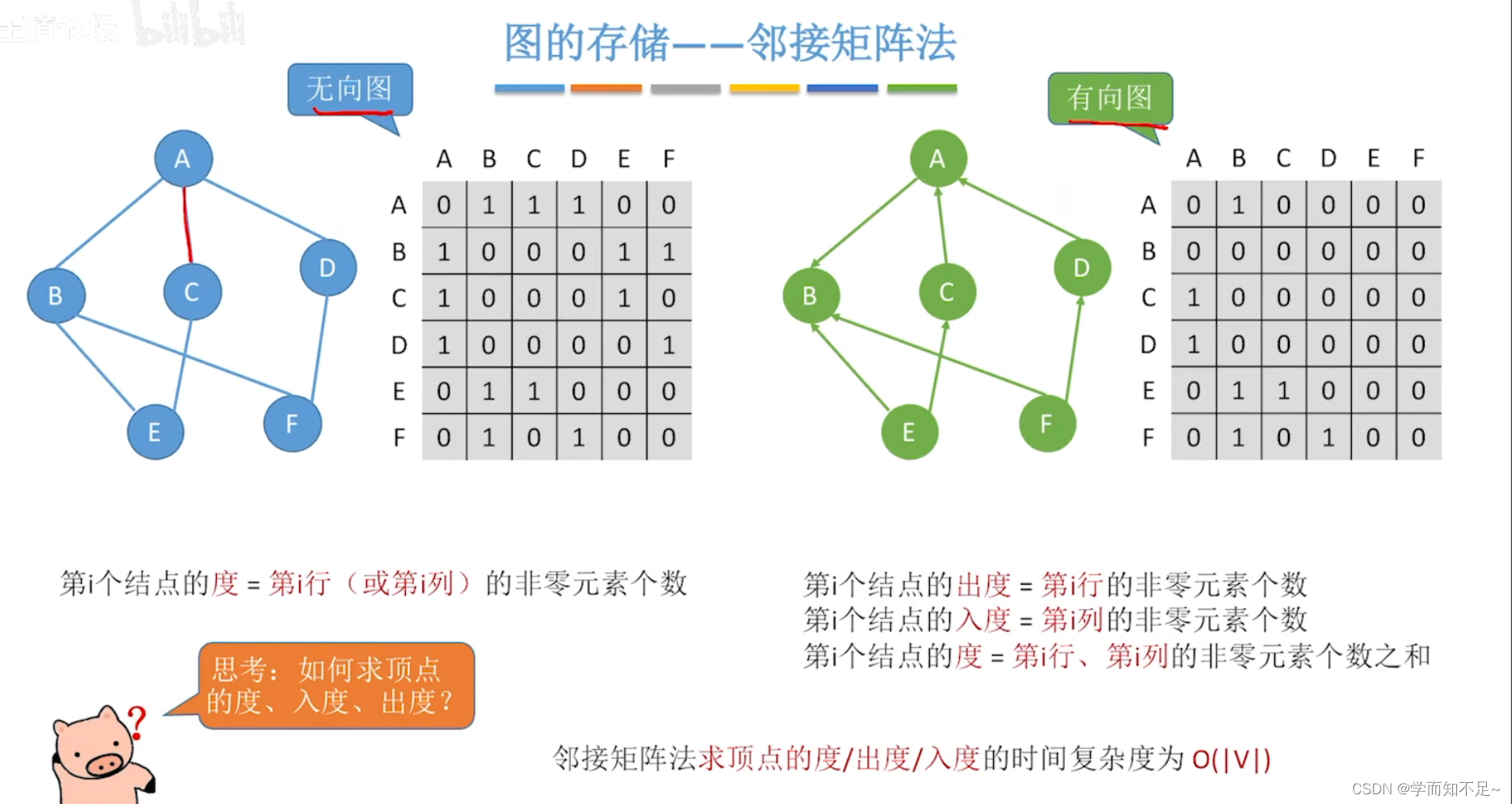
如何求顶点的度、入度、出度
带权图:
性能分析
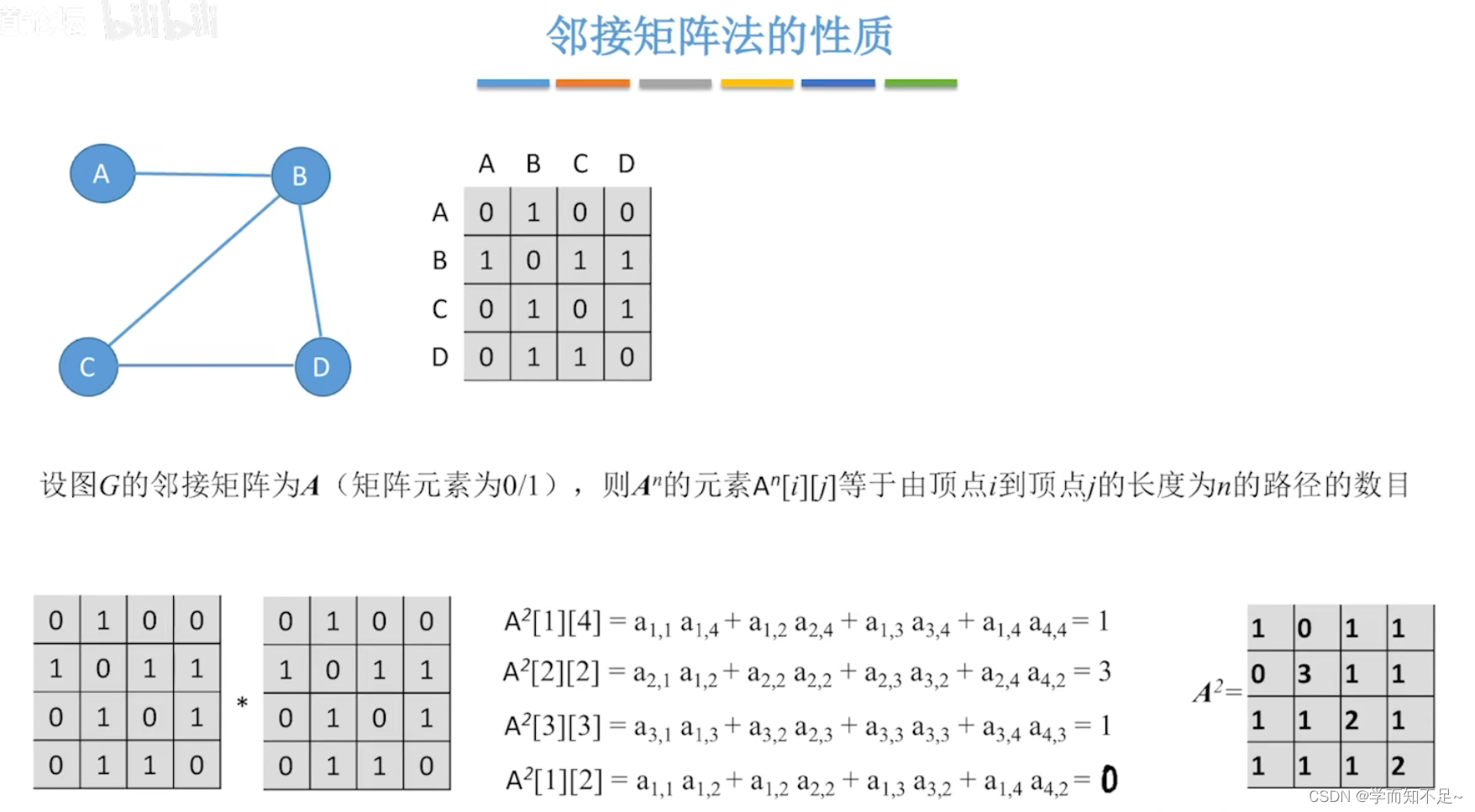
邻接矩阵的性质
行*列
邻接表
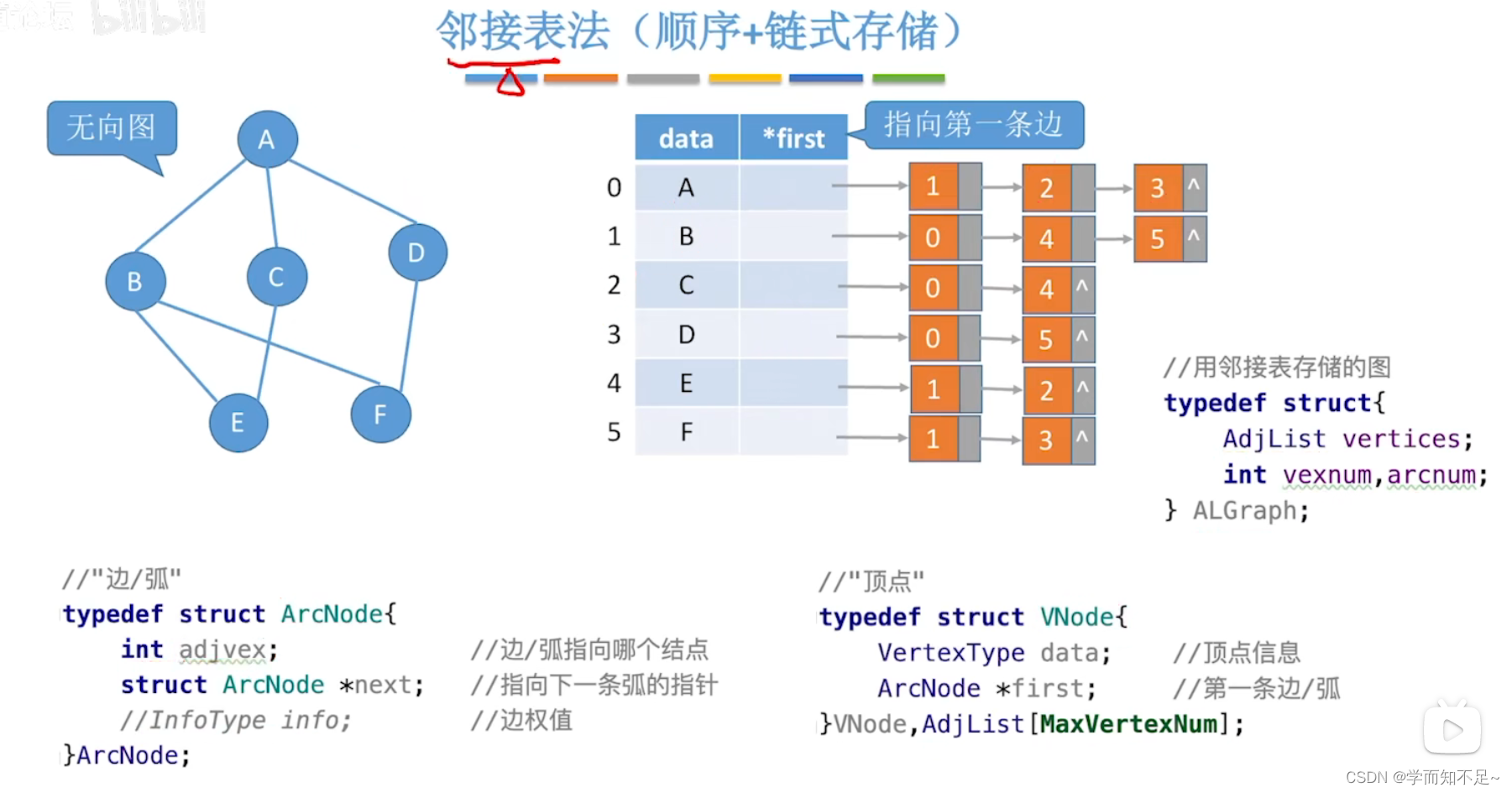
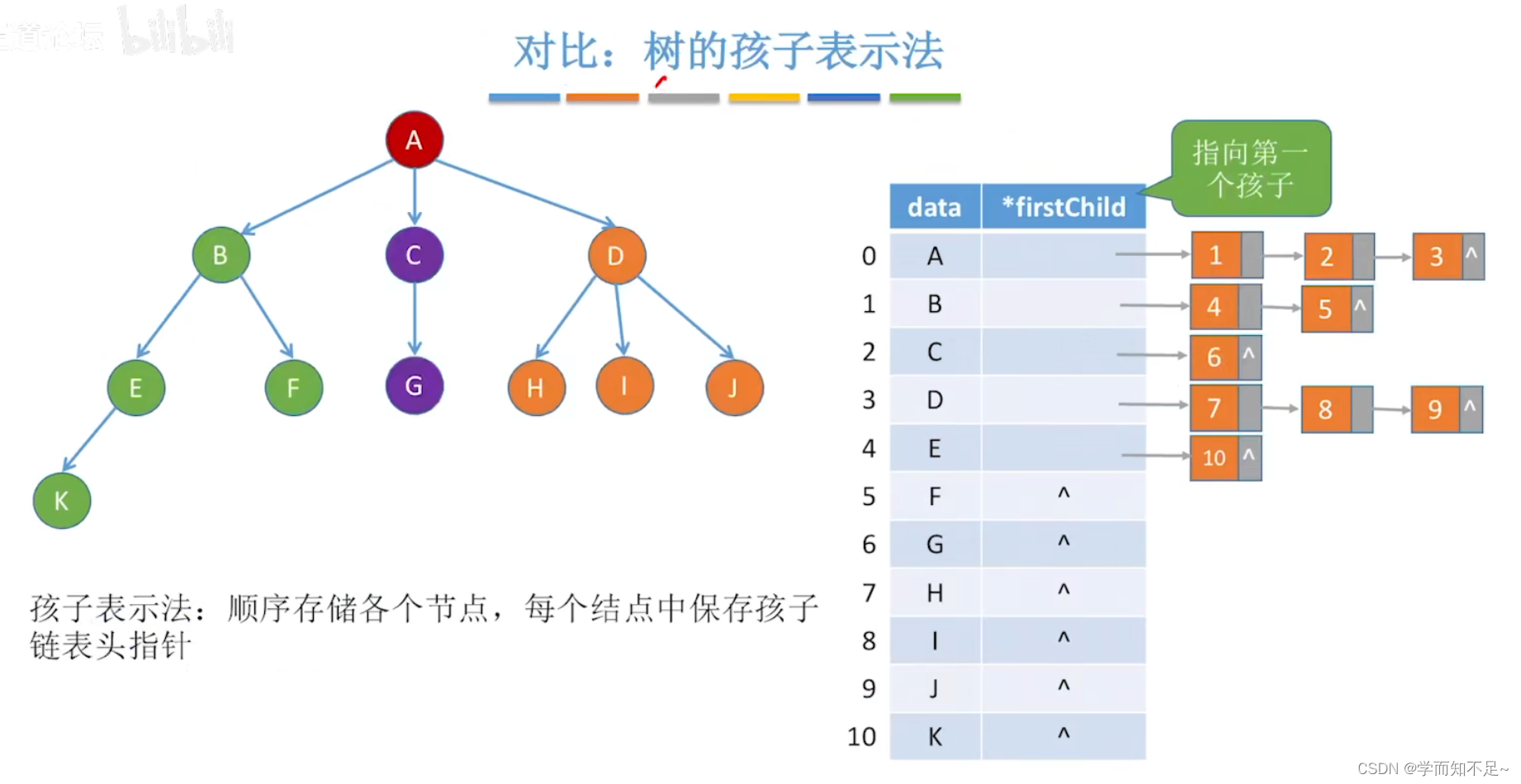
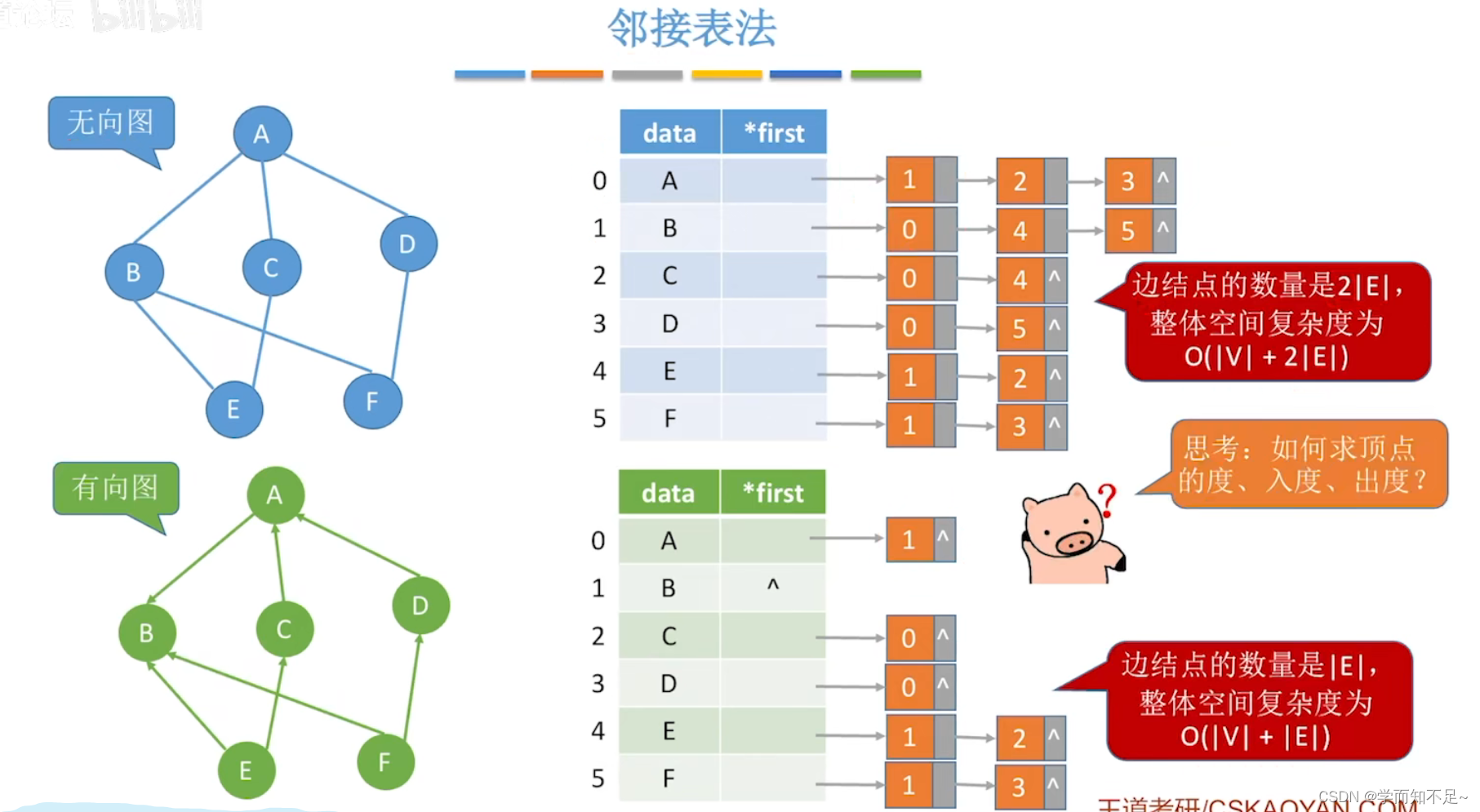
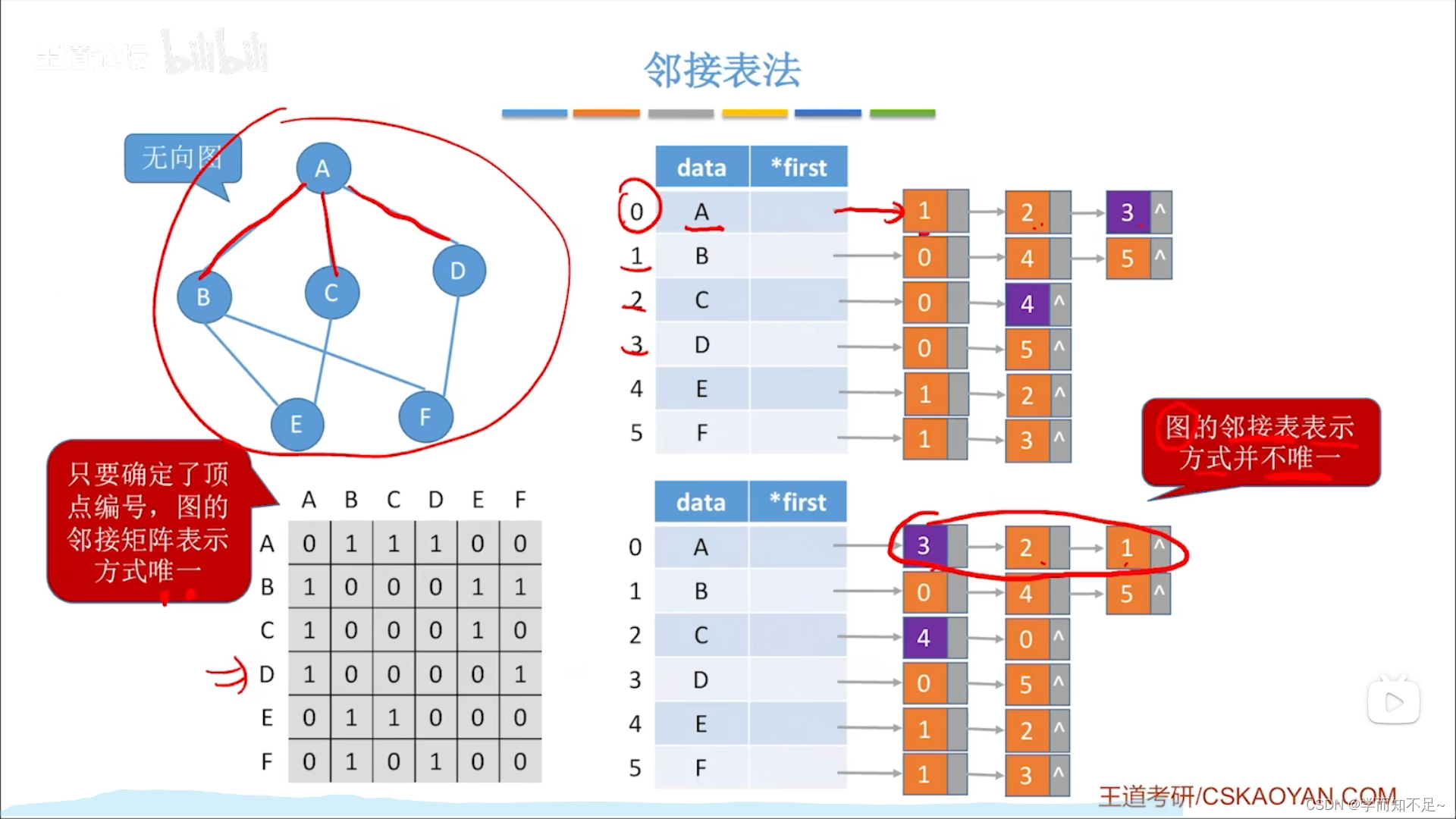
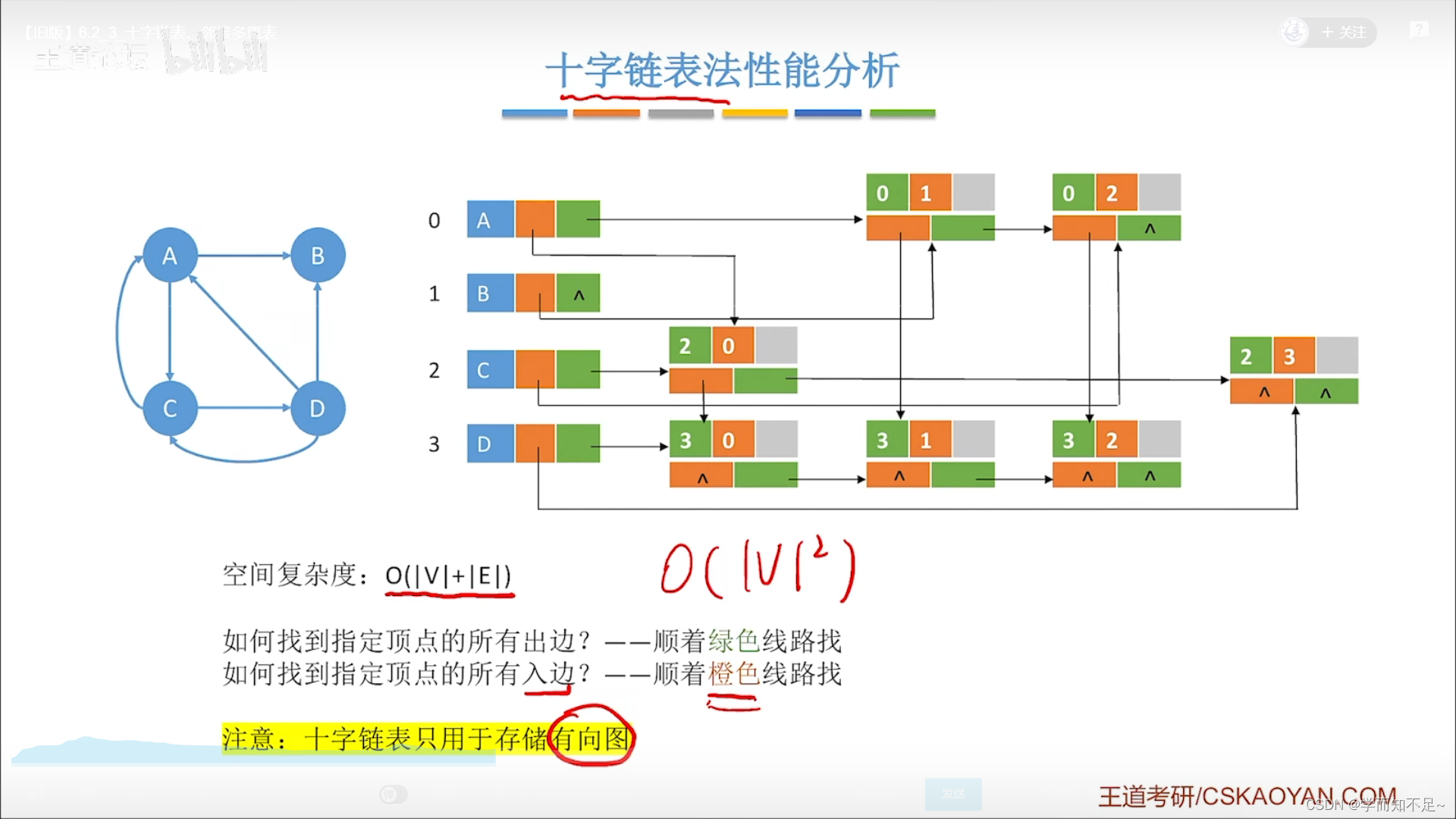
十字链表法
只能用于有向图
性能分析
邻接多重表
只用于存储无向图
总结
图的操作

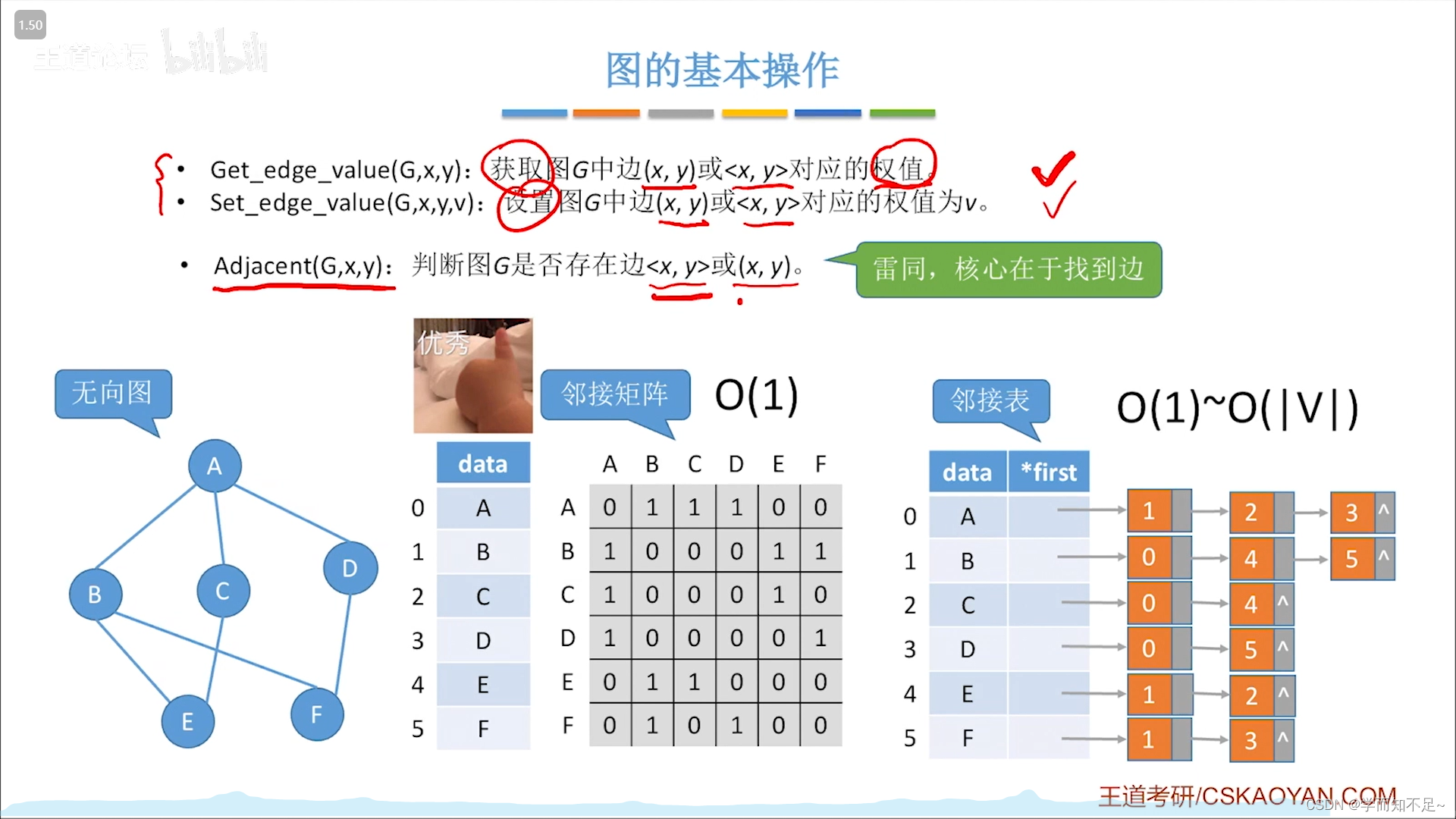
判断图中是否有某条边
无向图:
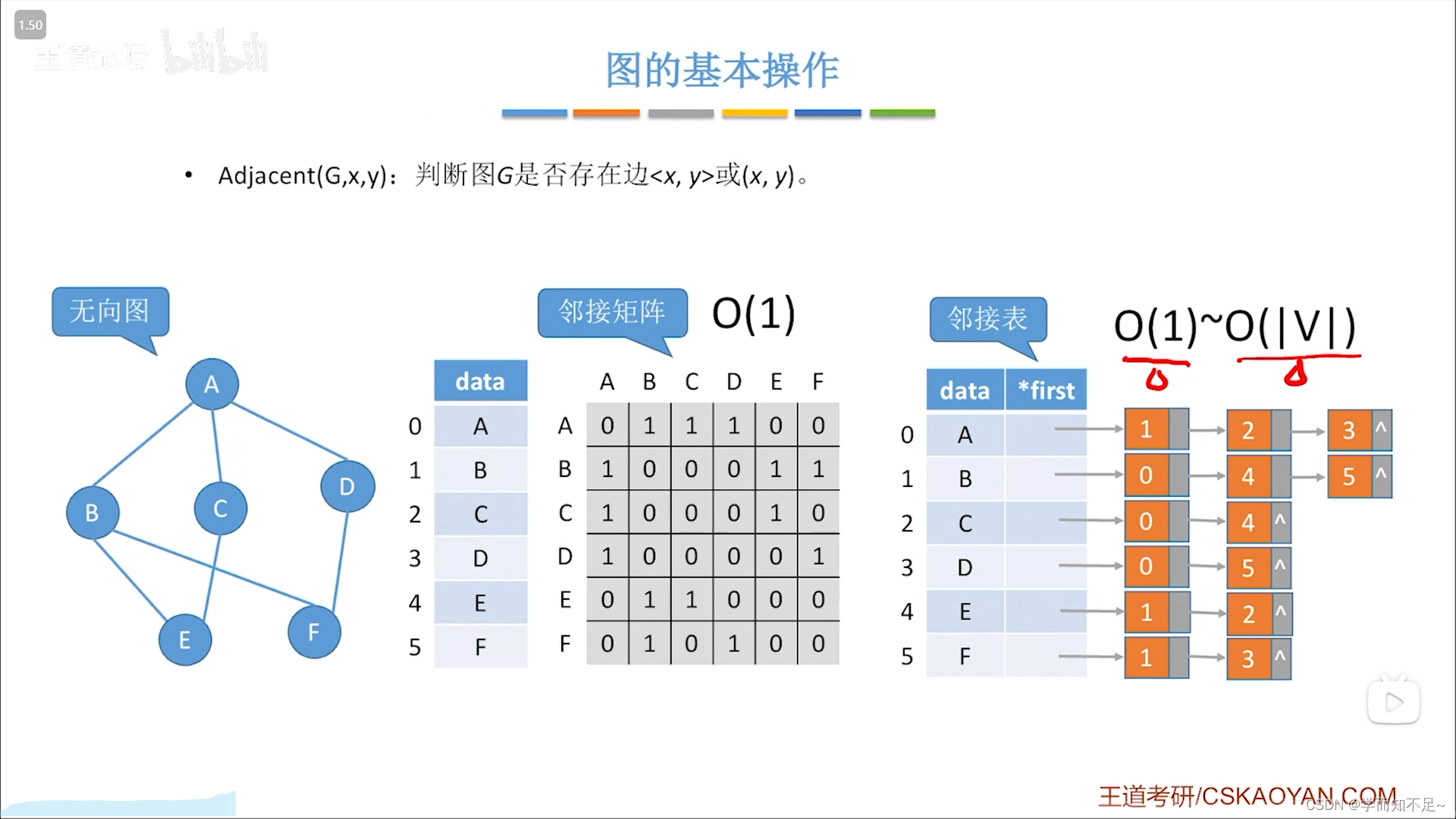
有向图:

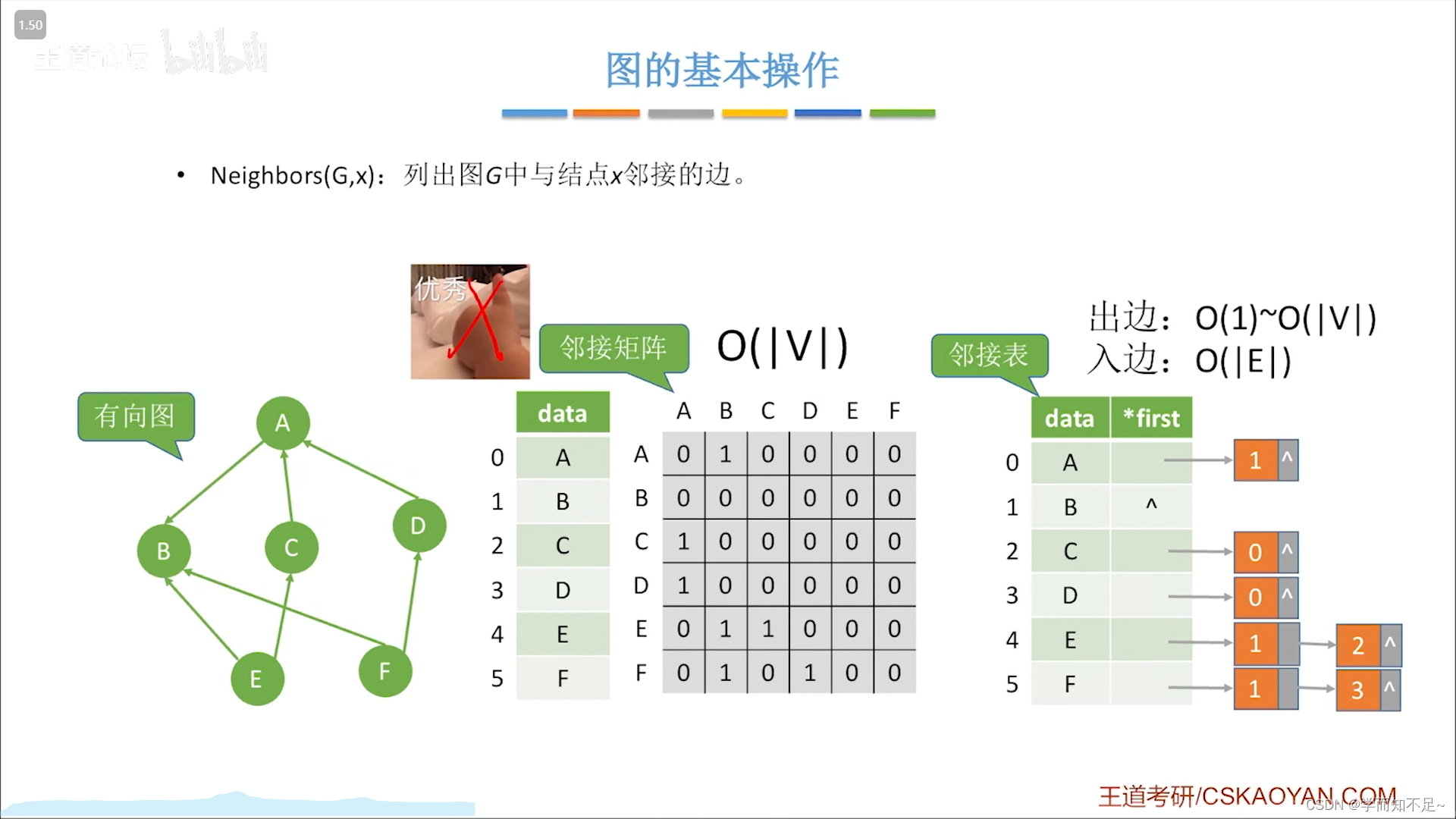
列出图中与结点邻接的所有边
无向图:
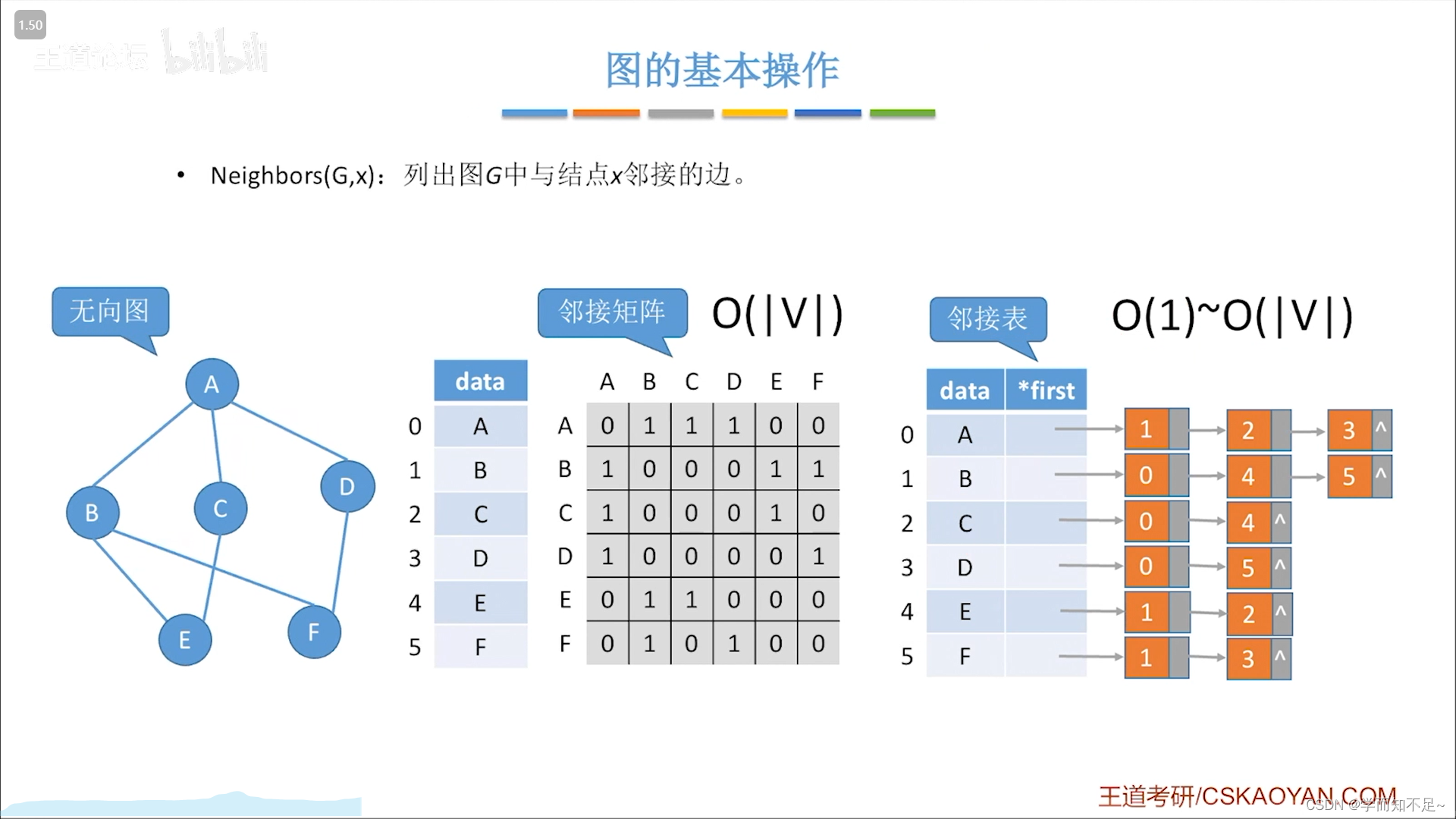
有向图:
在图中插入顶点
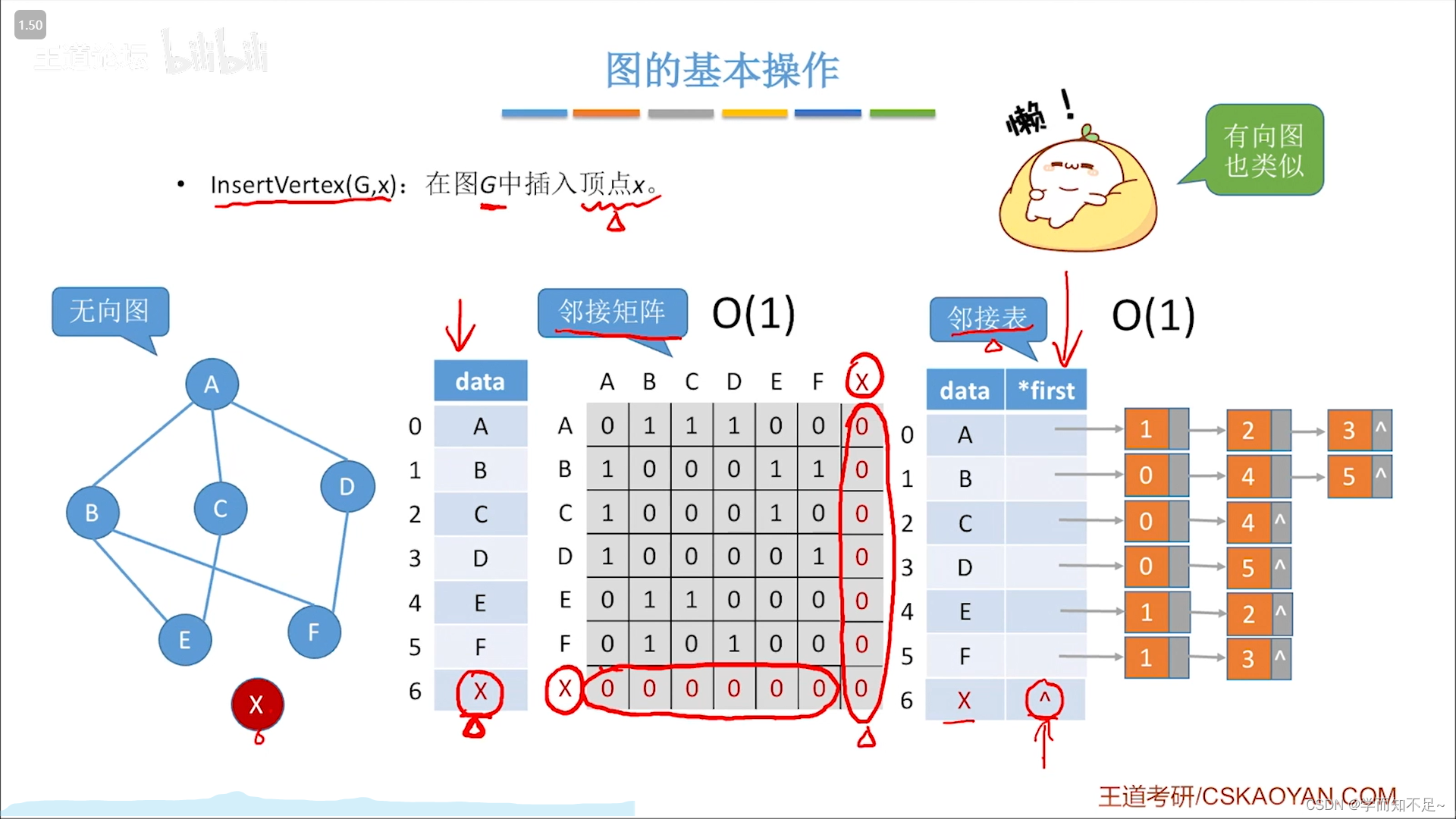
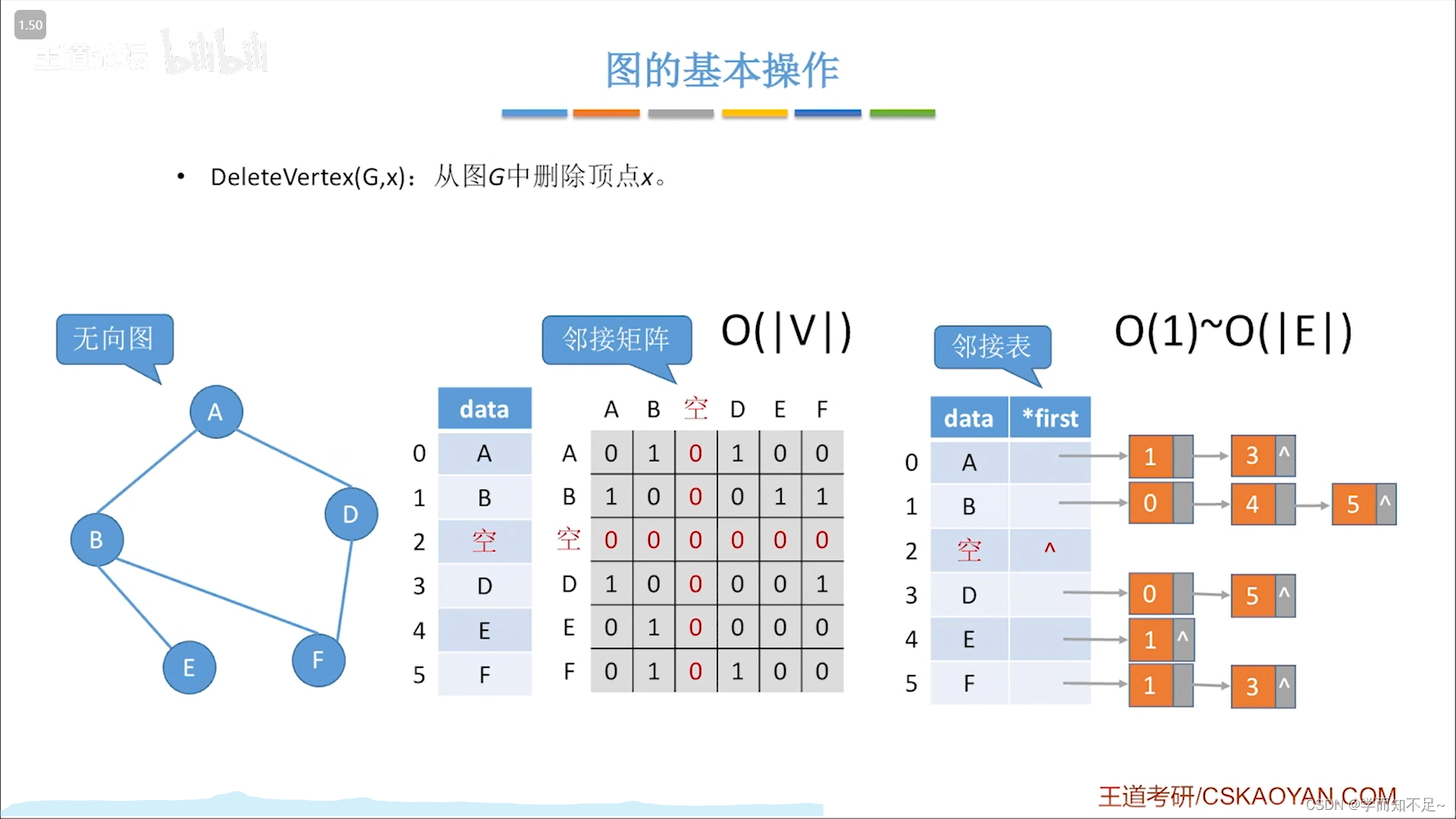
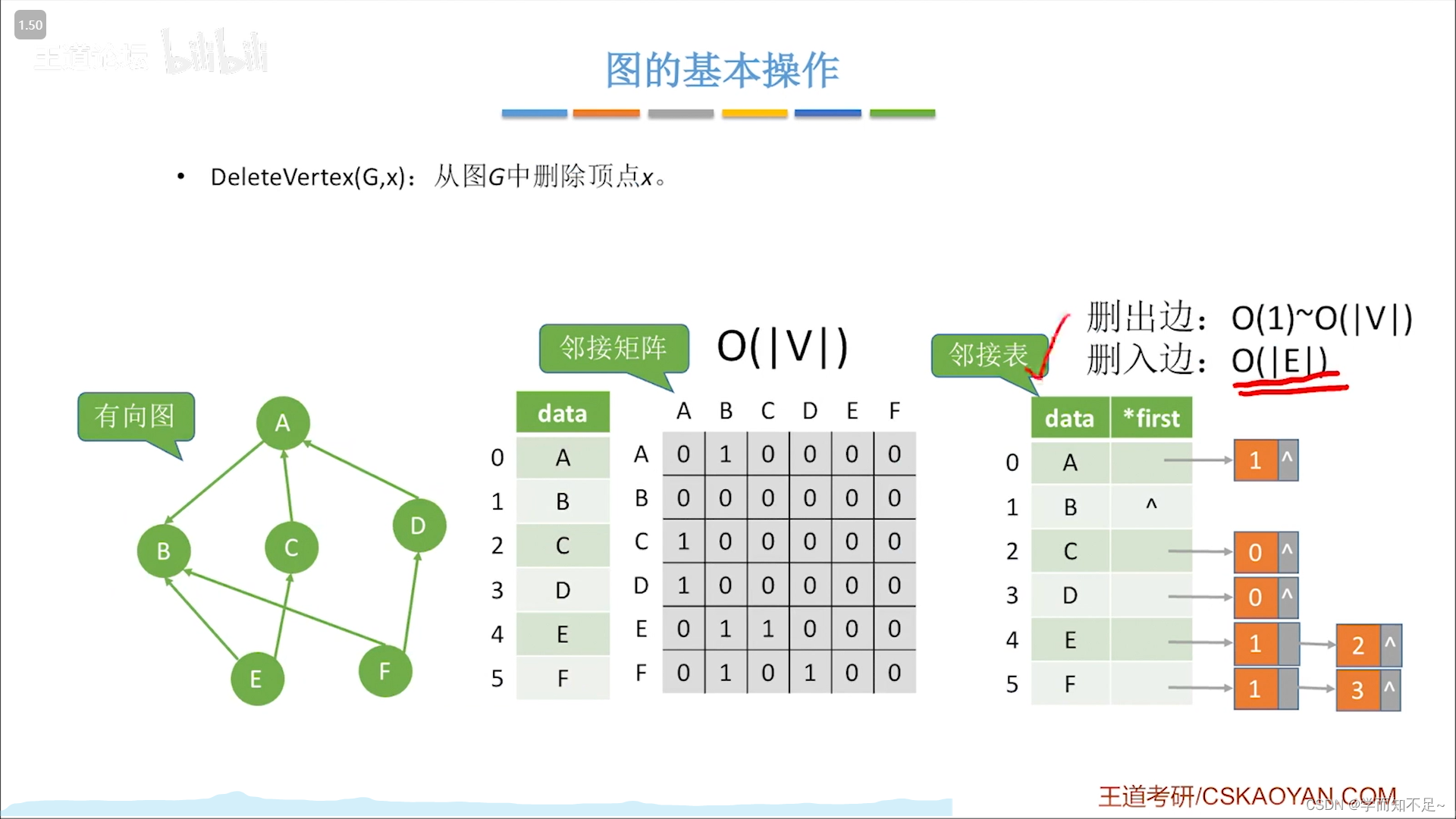
在图中删除顶点
无向图:
有向图:
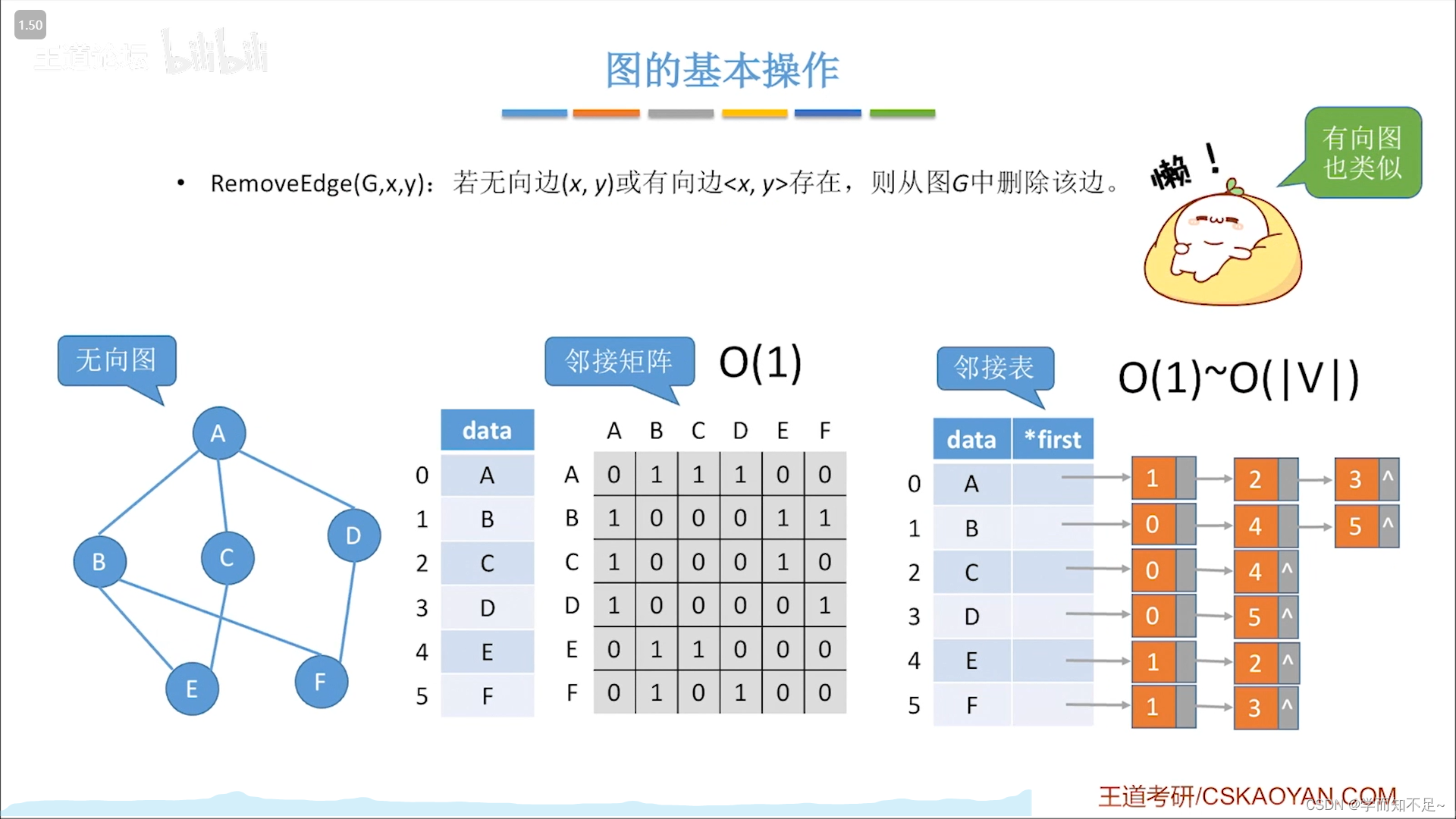
向图中添加一条边
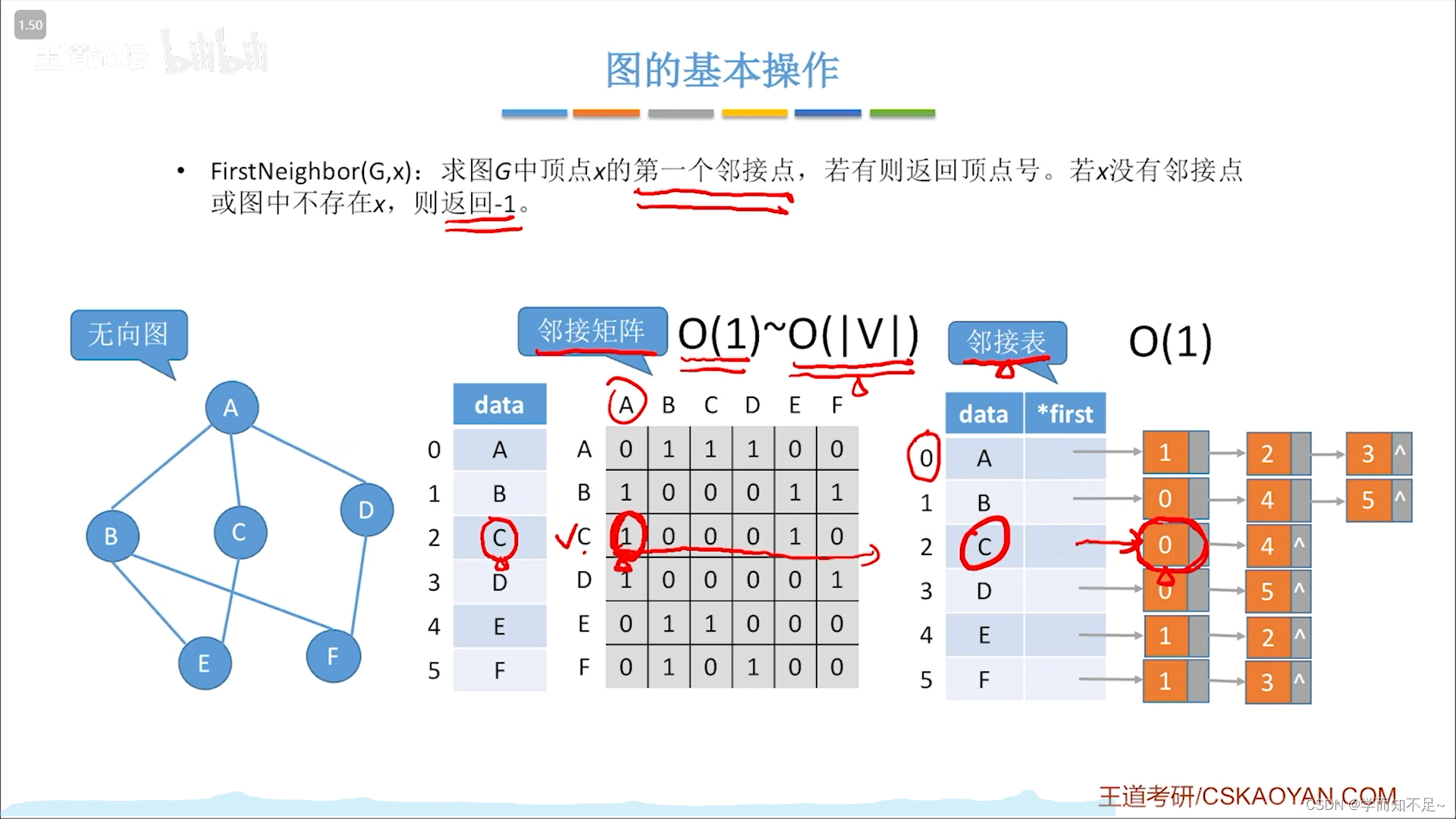
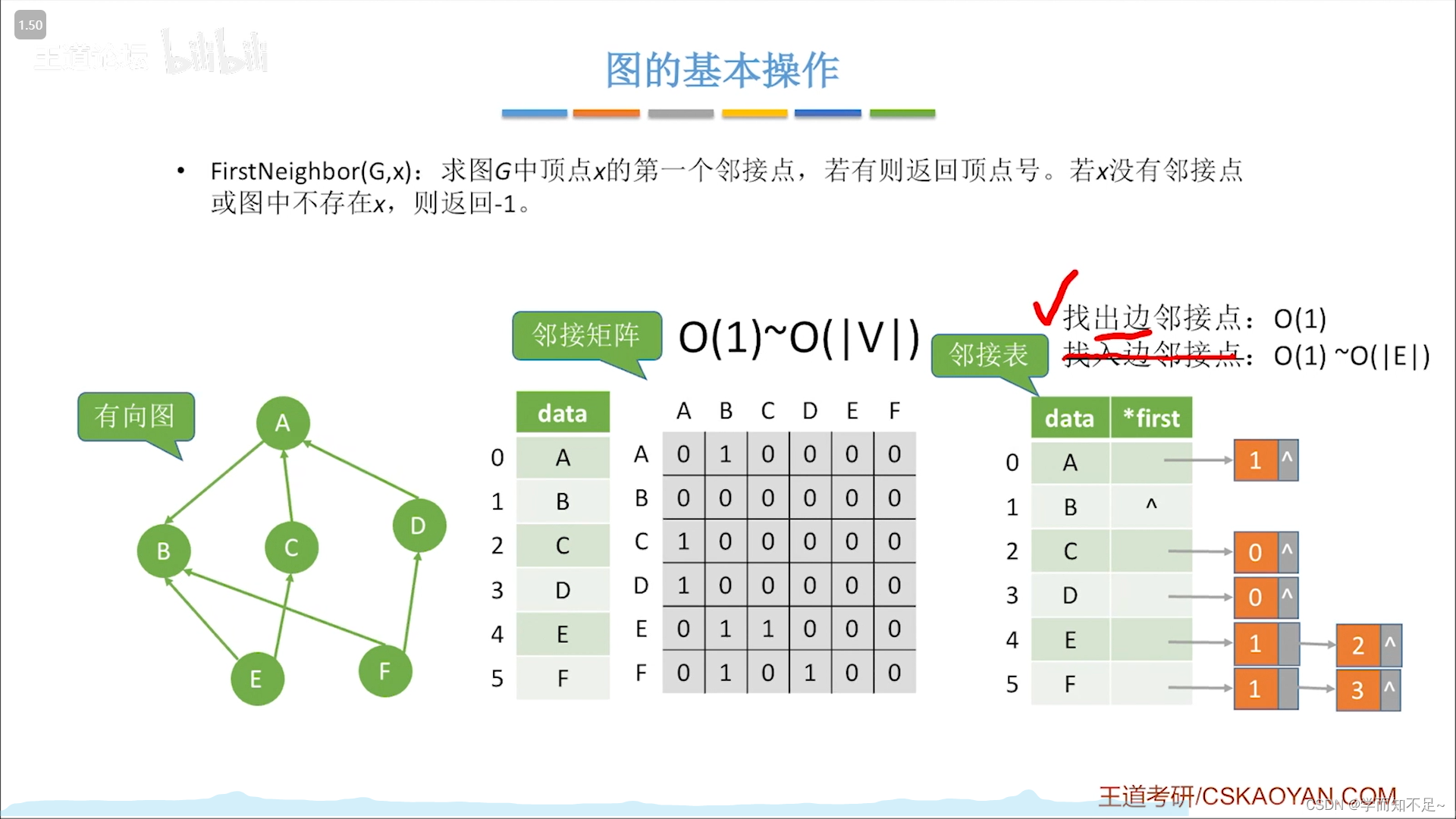
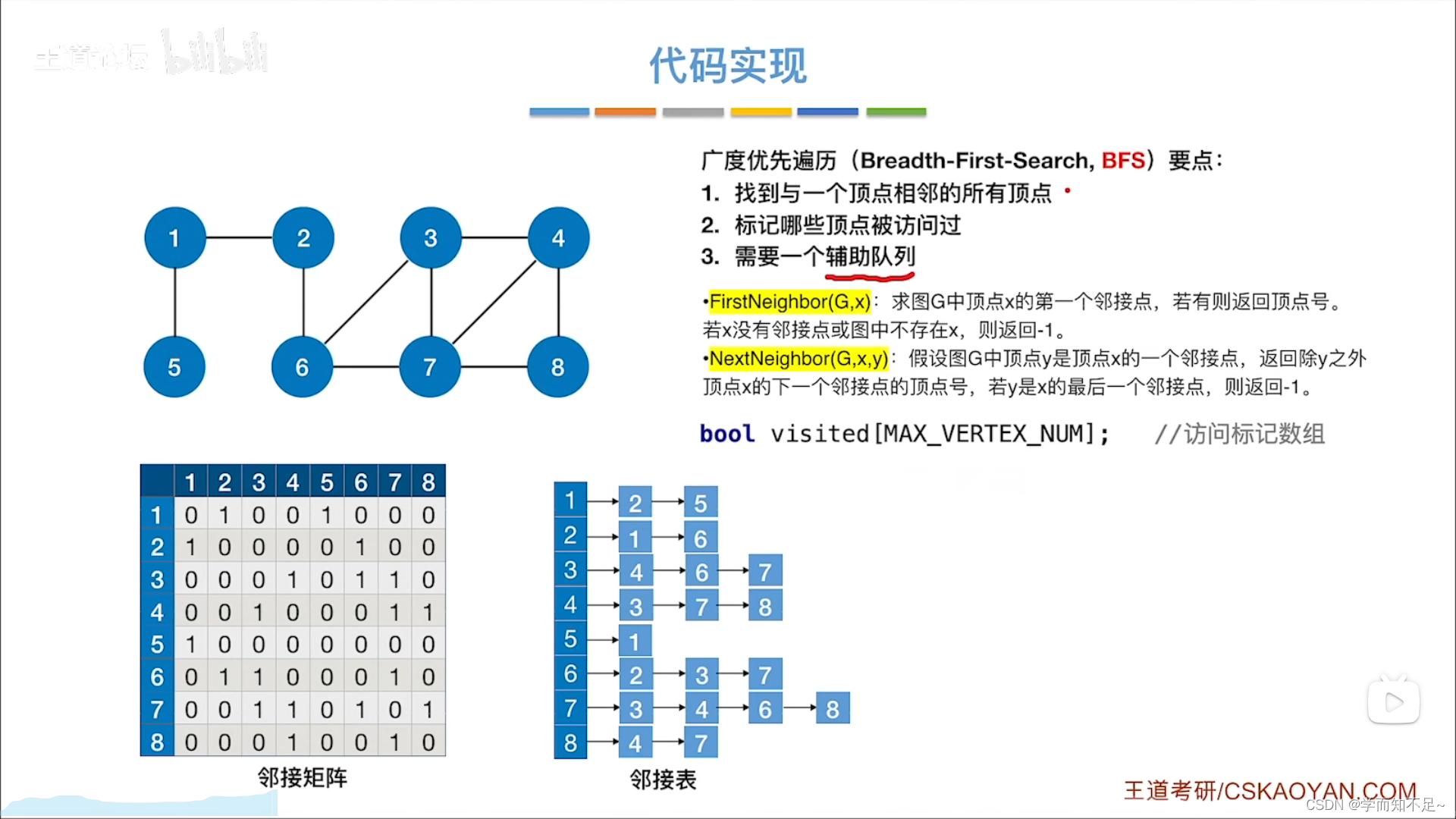
求图中顶点x的第一个邻接点
无向图:
有向图:
假设图中顶点x的一个邻接点y,返回除y之外顶点x 的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1
无向图:

获取并设置图中边的权值
图的遍历
- 广度优先遍历
- 深度优先遍历
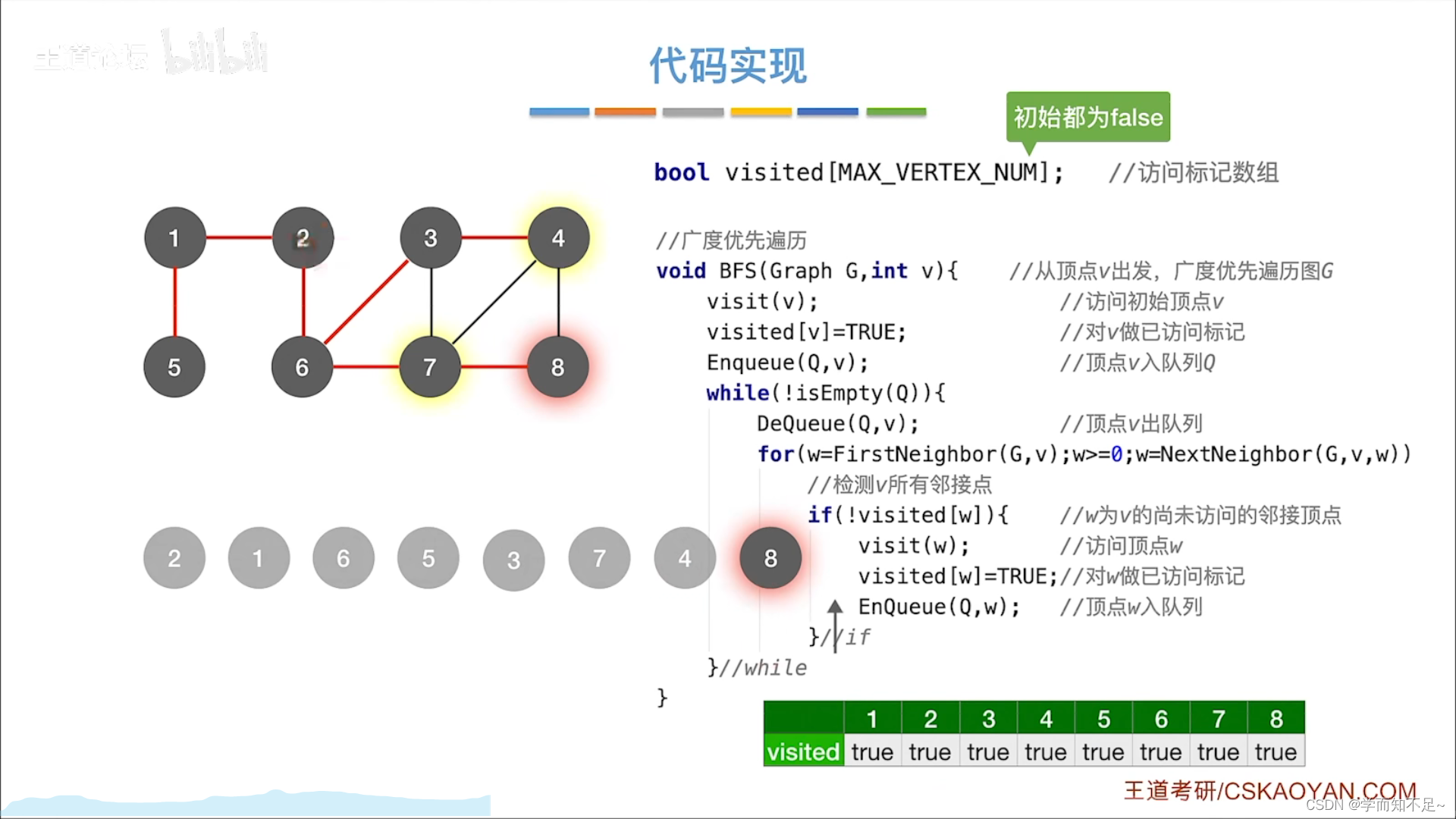
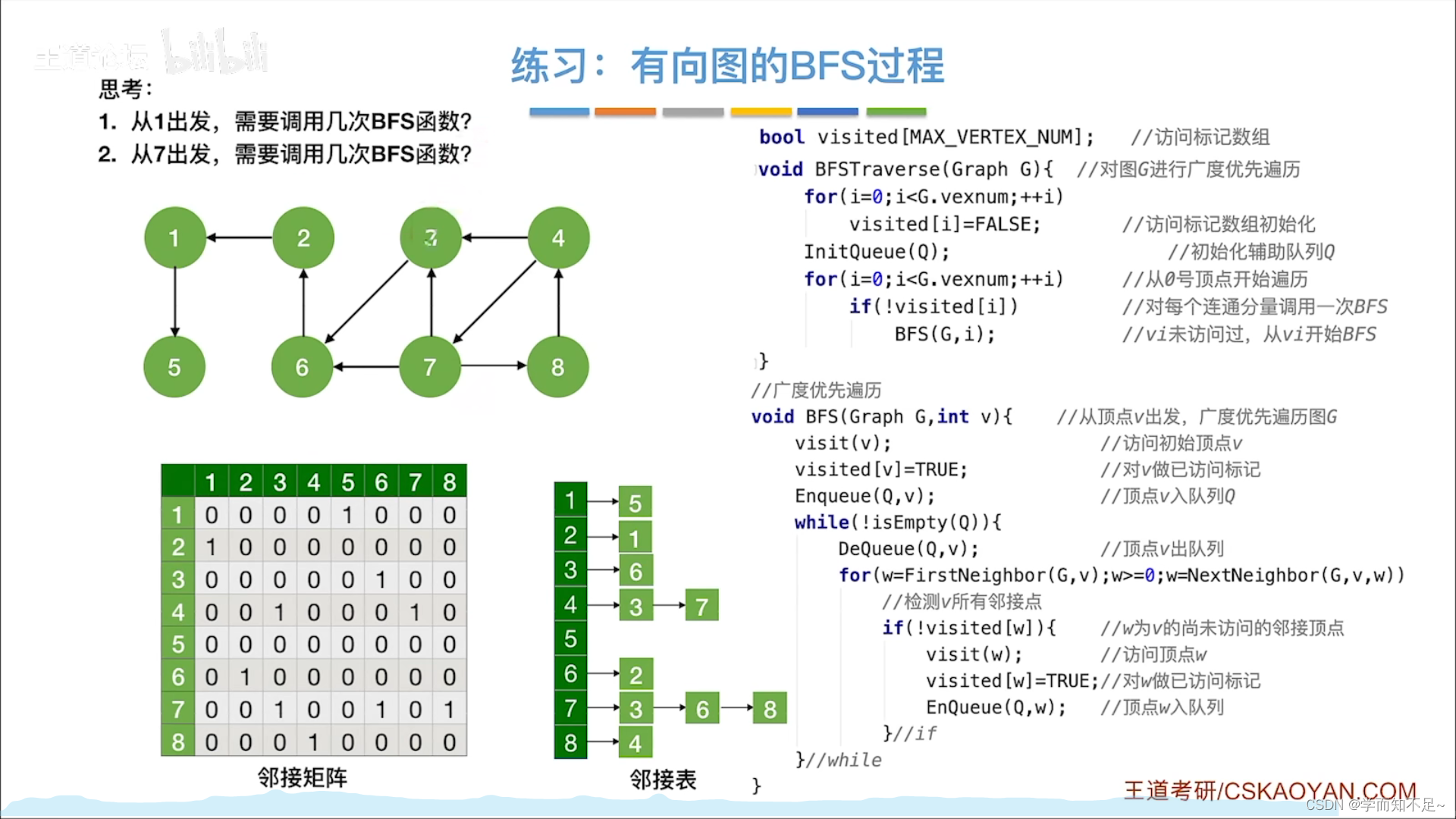
广度优先遍历
代码实现
遍历序列的可变性
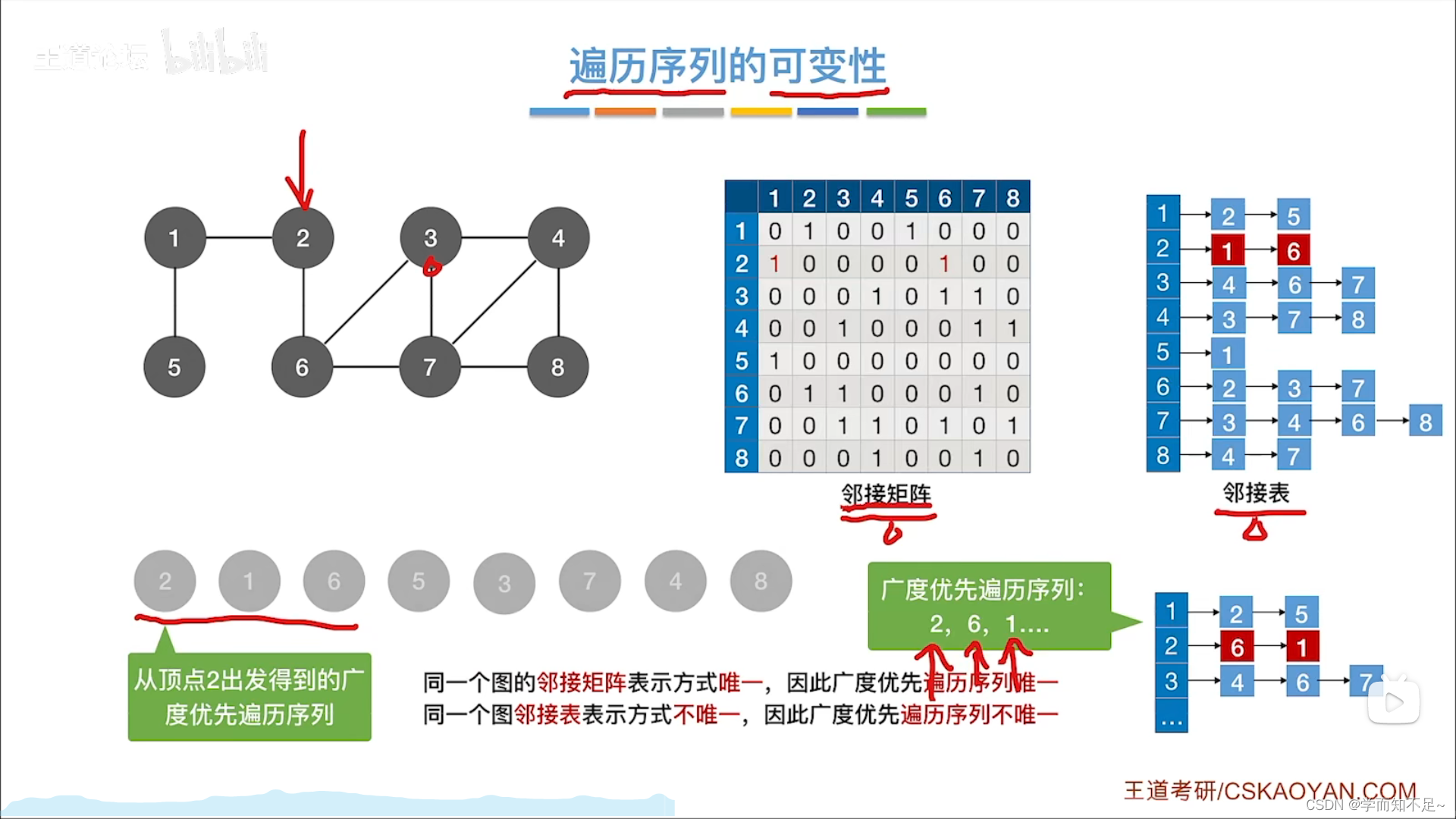
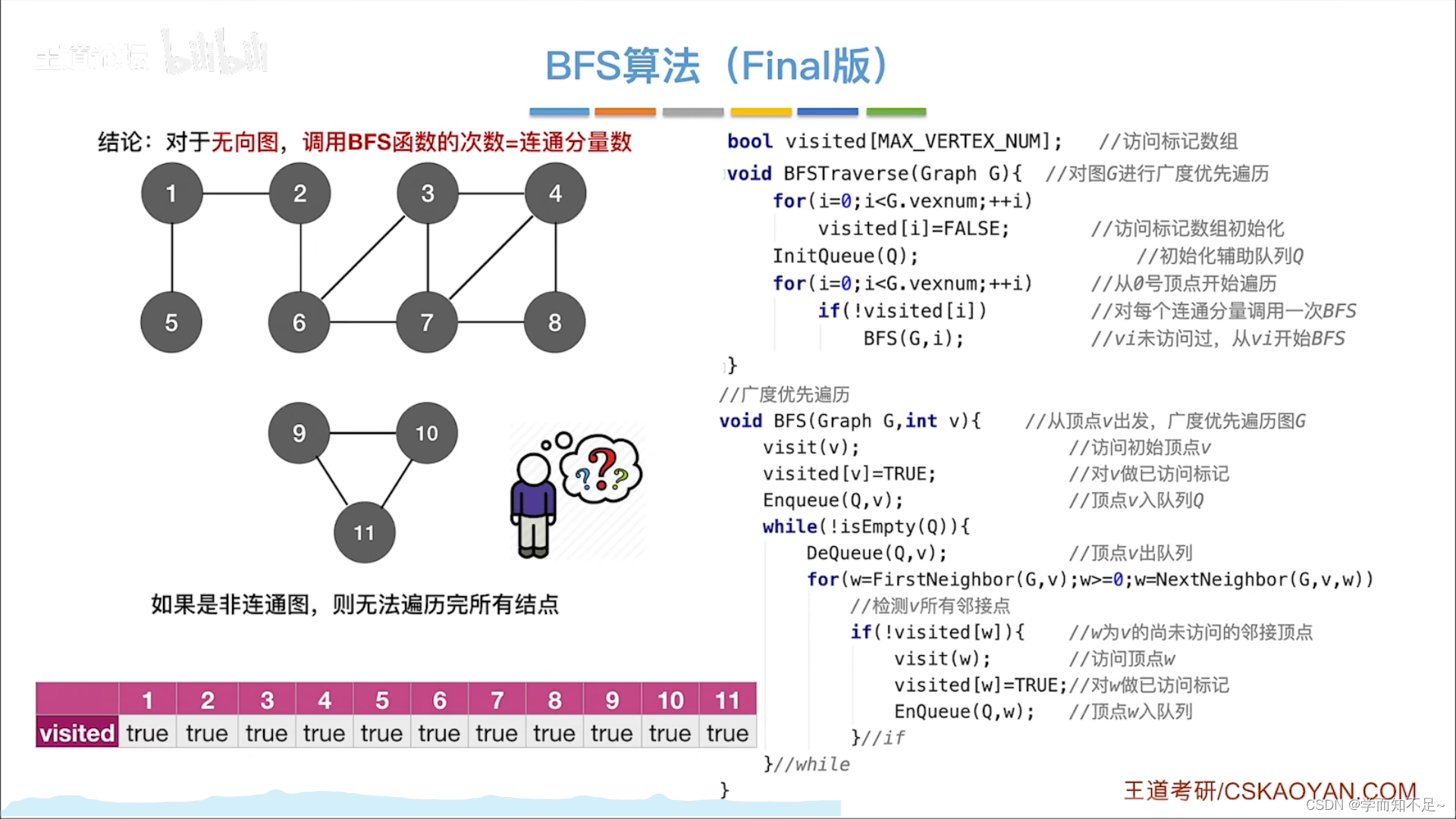
算法改进
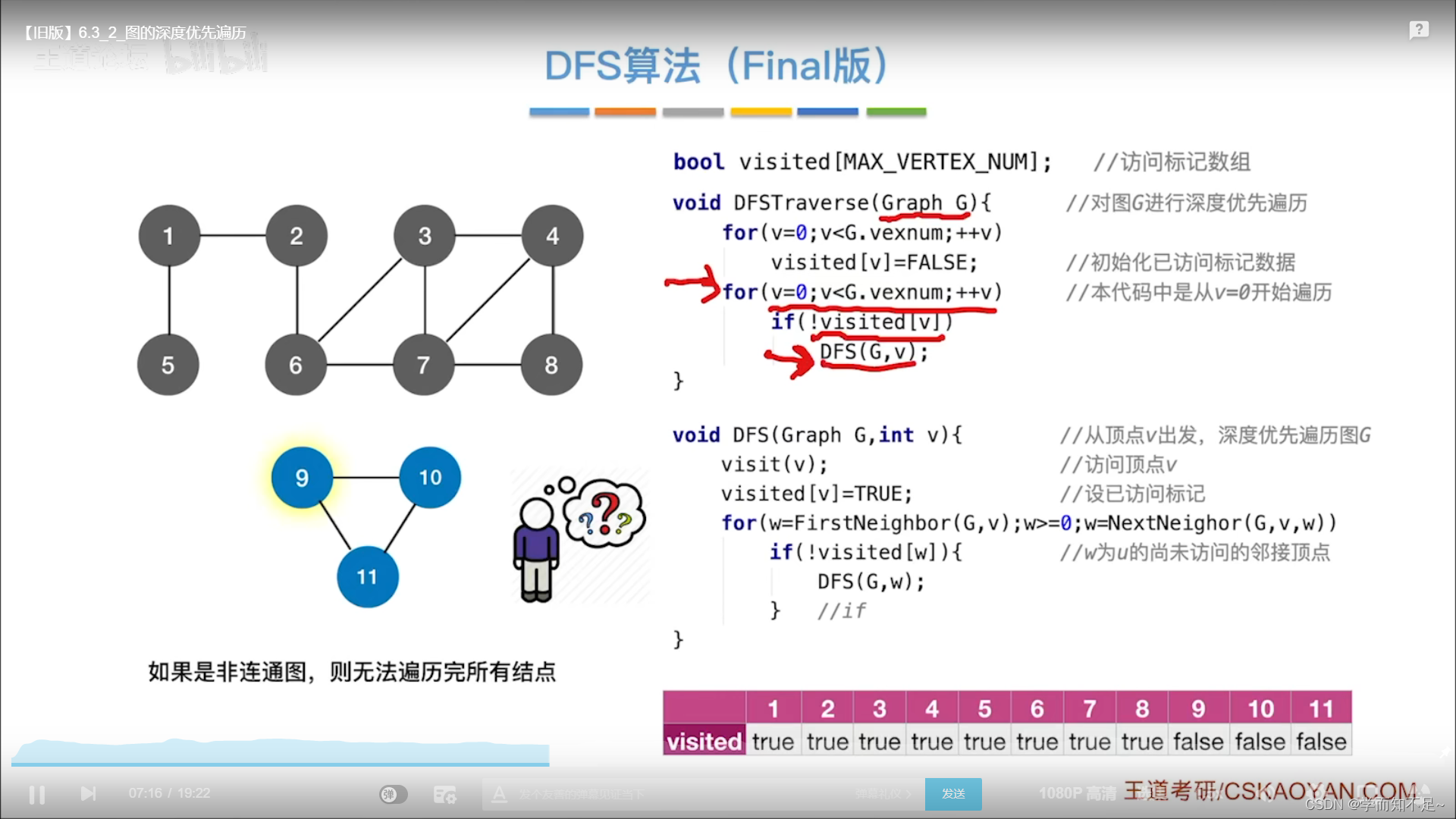
因为如果是非连通图,则无法遍历完所有结点
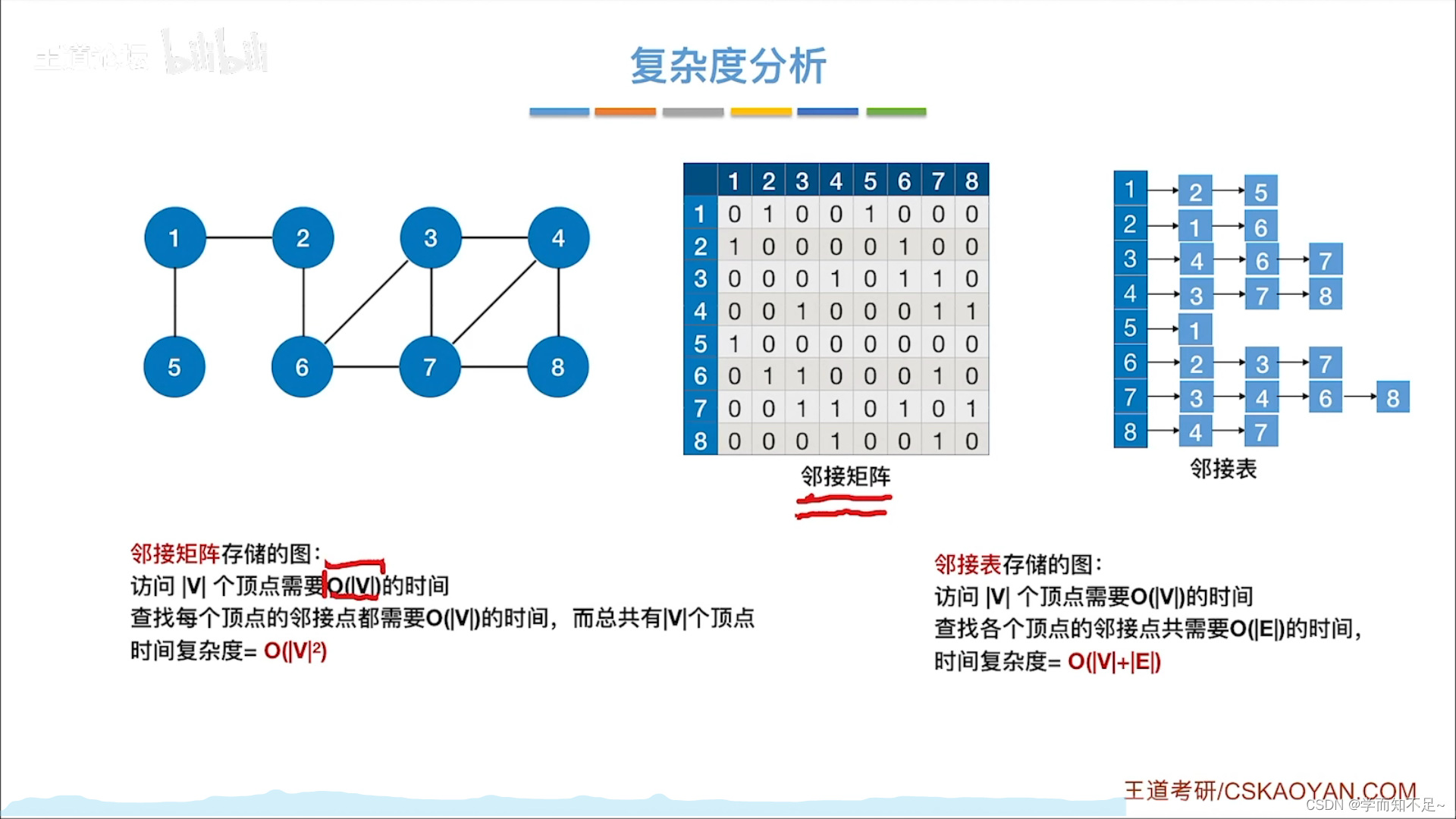
复杂度分析
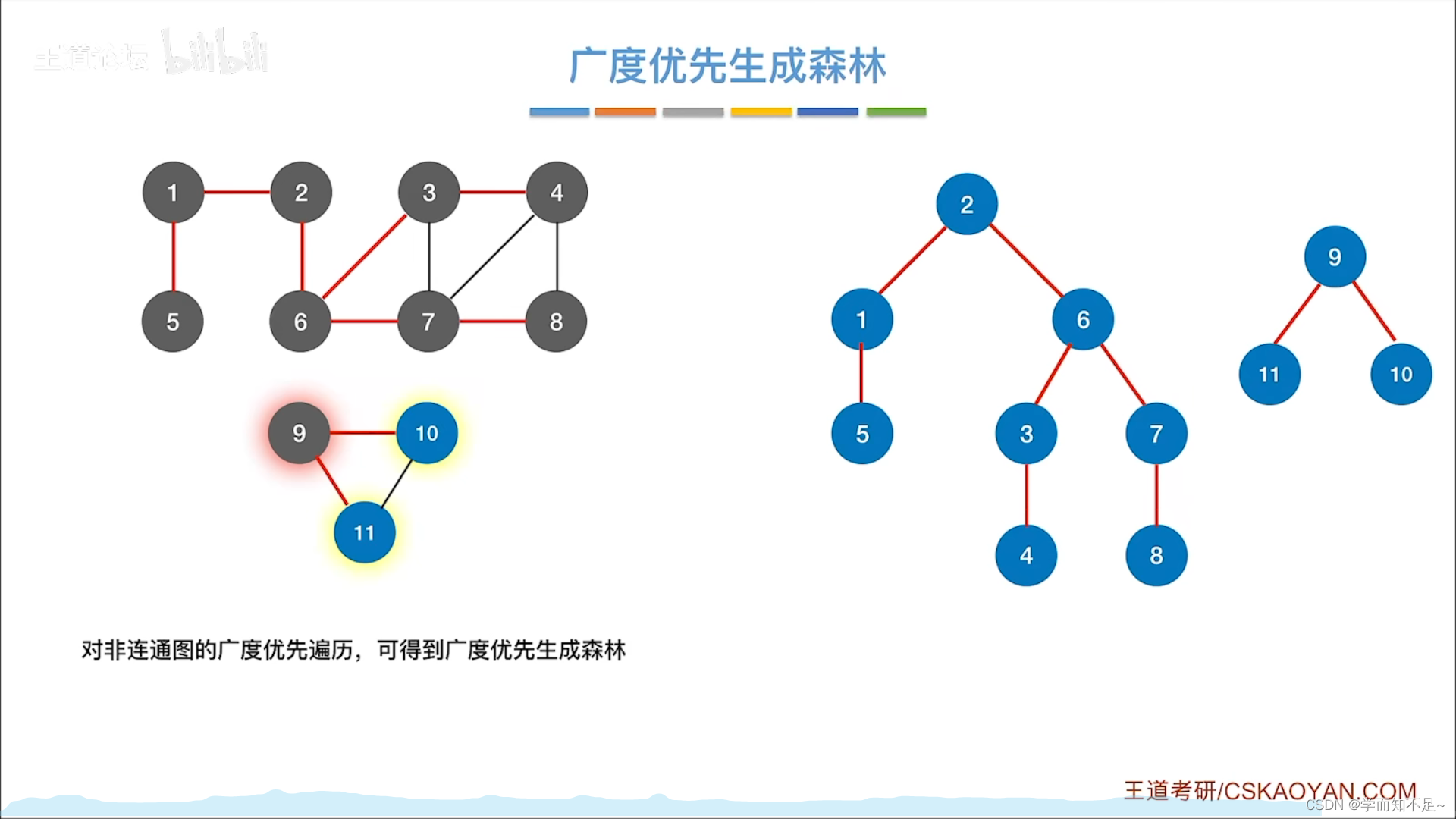
广度优先生成树

广度优先生成森林
练习
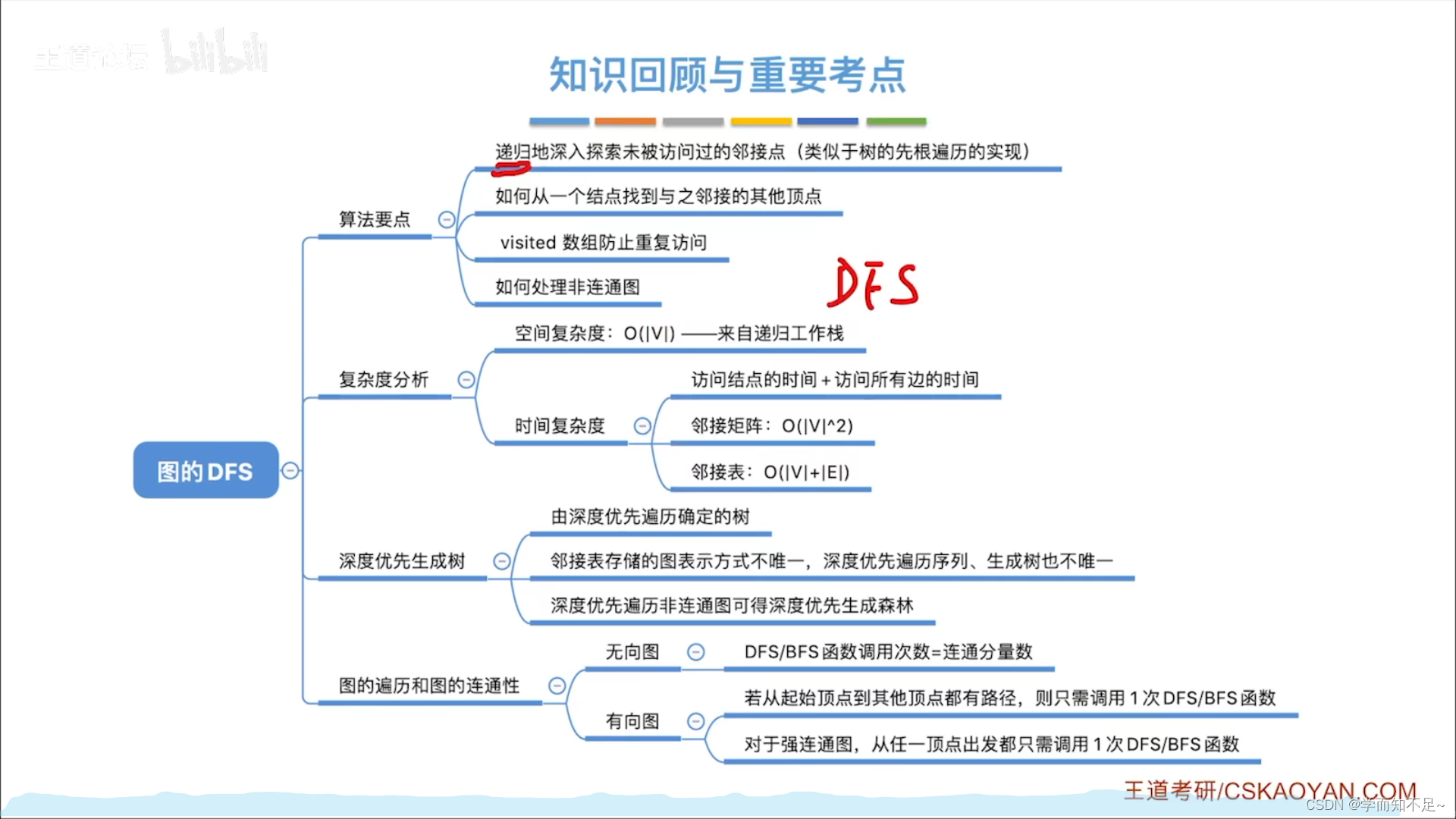
深度优先遍历
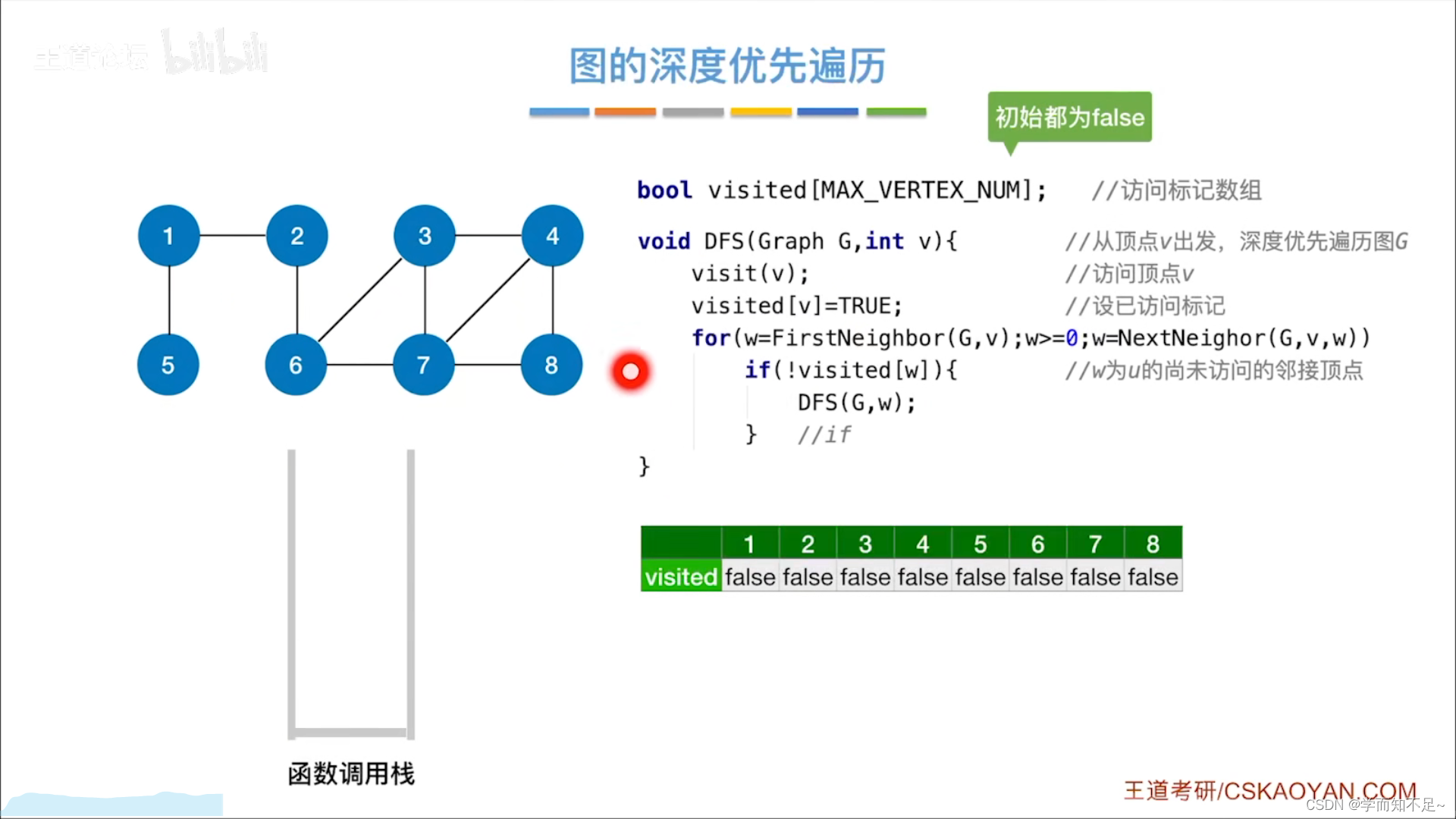
算法改进
复杂度分析
空间复杂度:
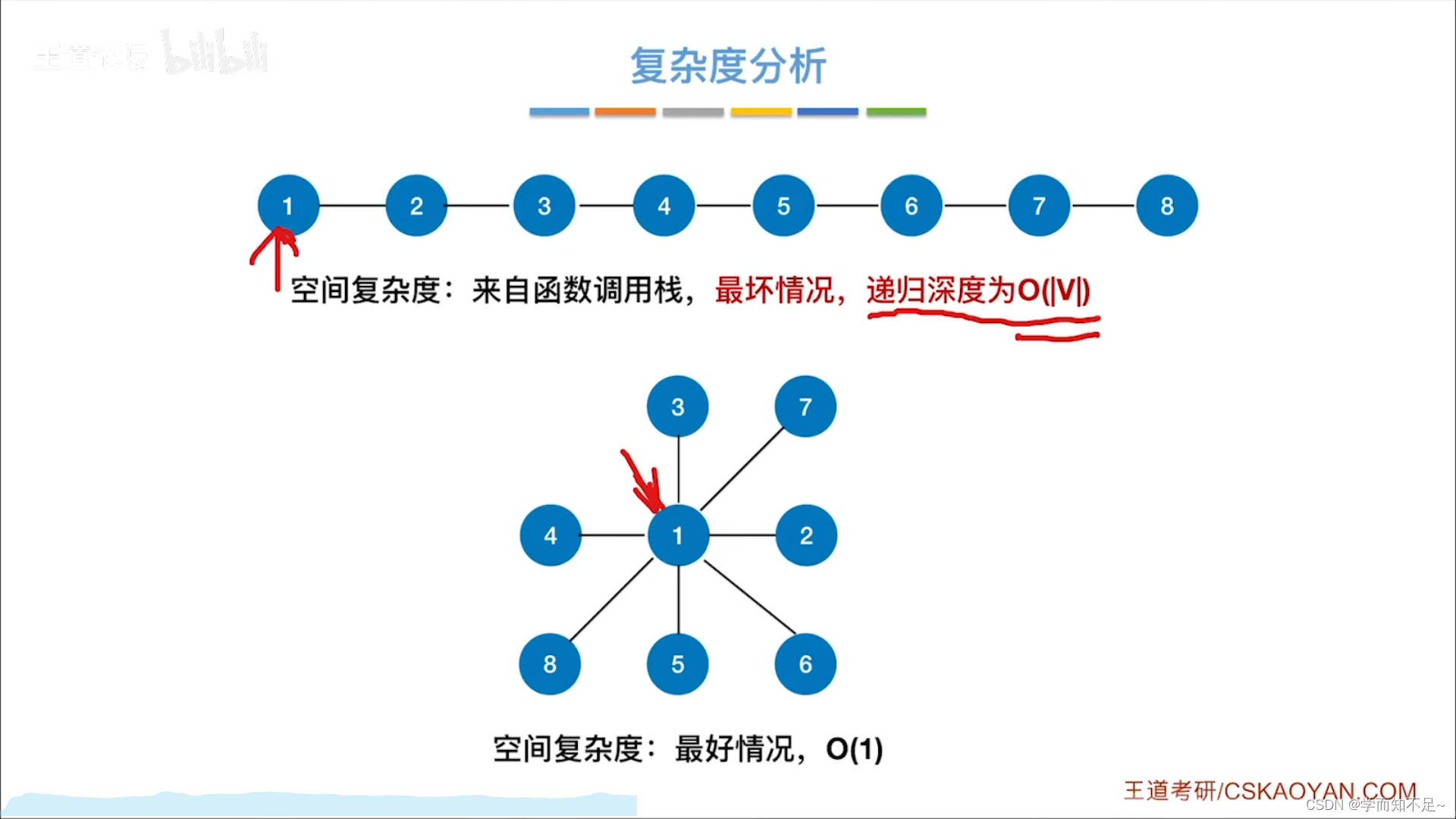
时间复杂度:

深度优先生成树
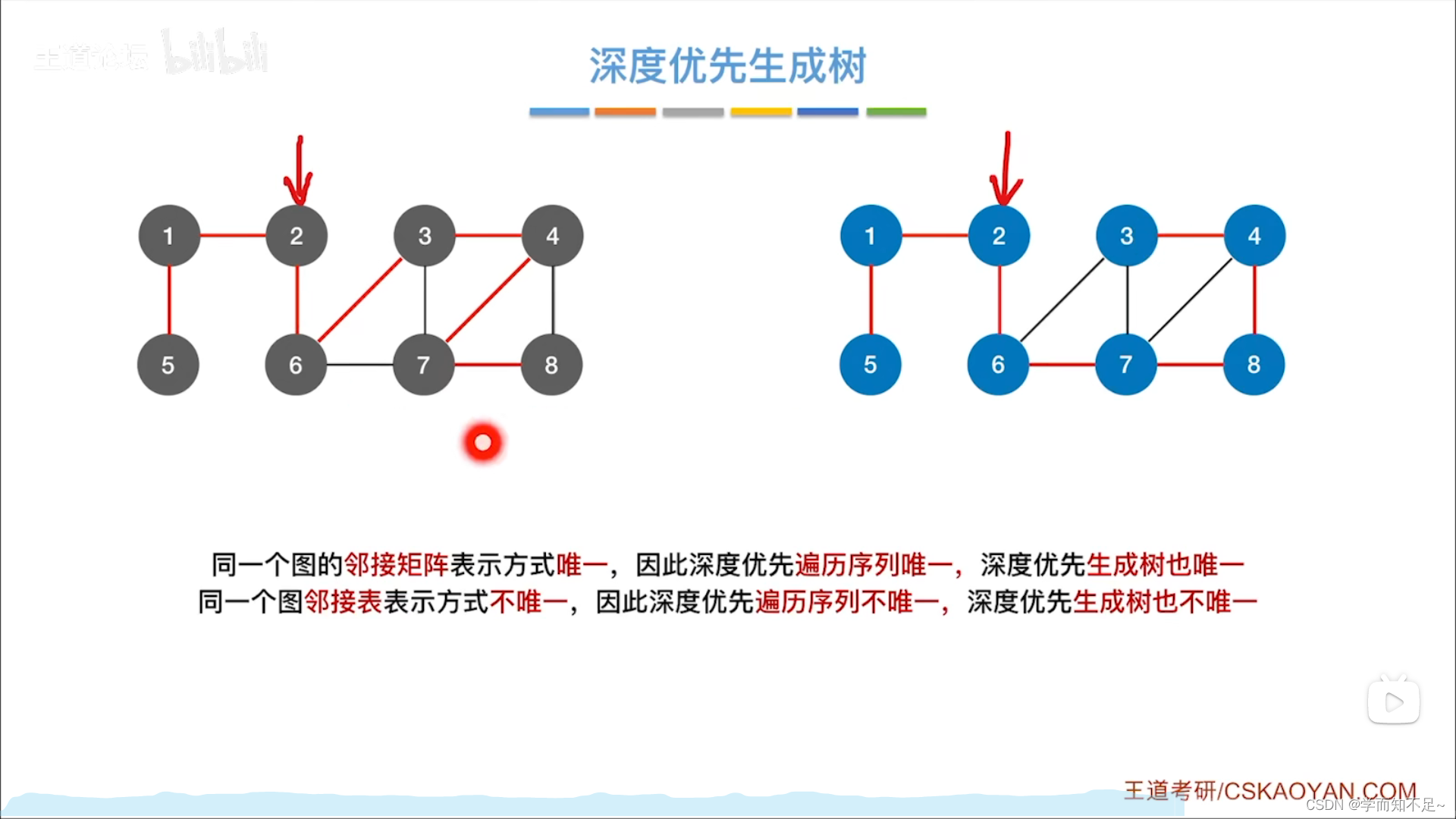
深度优先生成森林

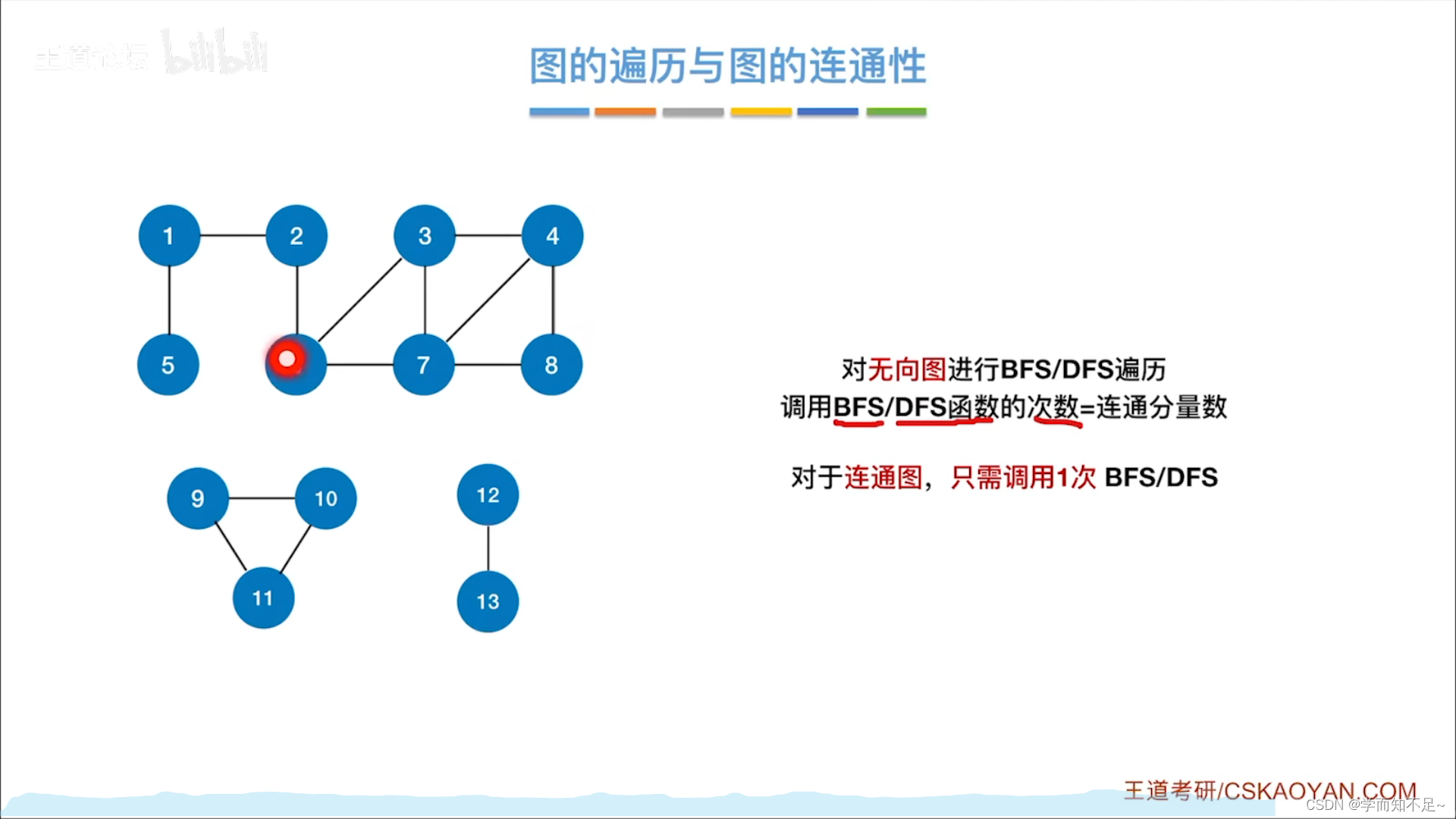
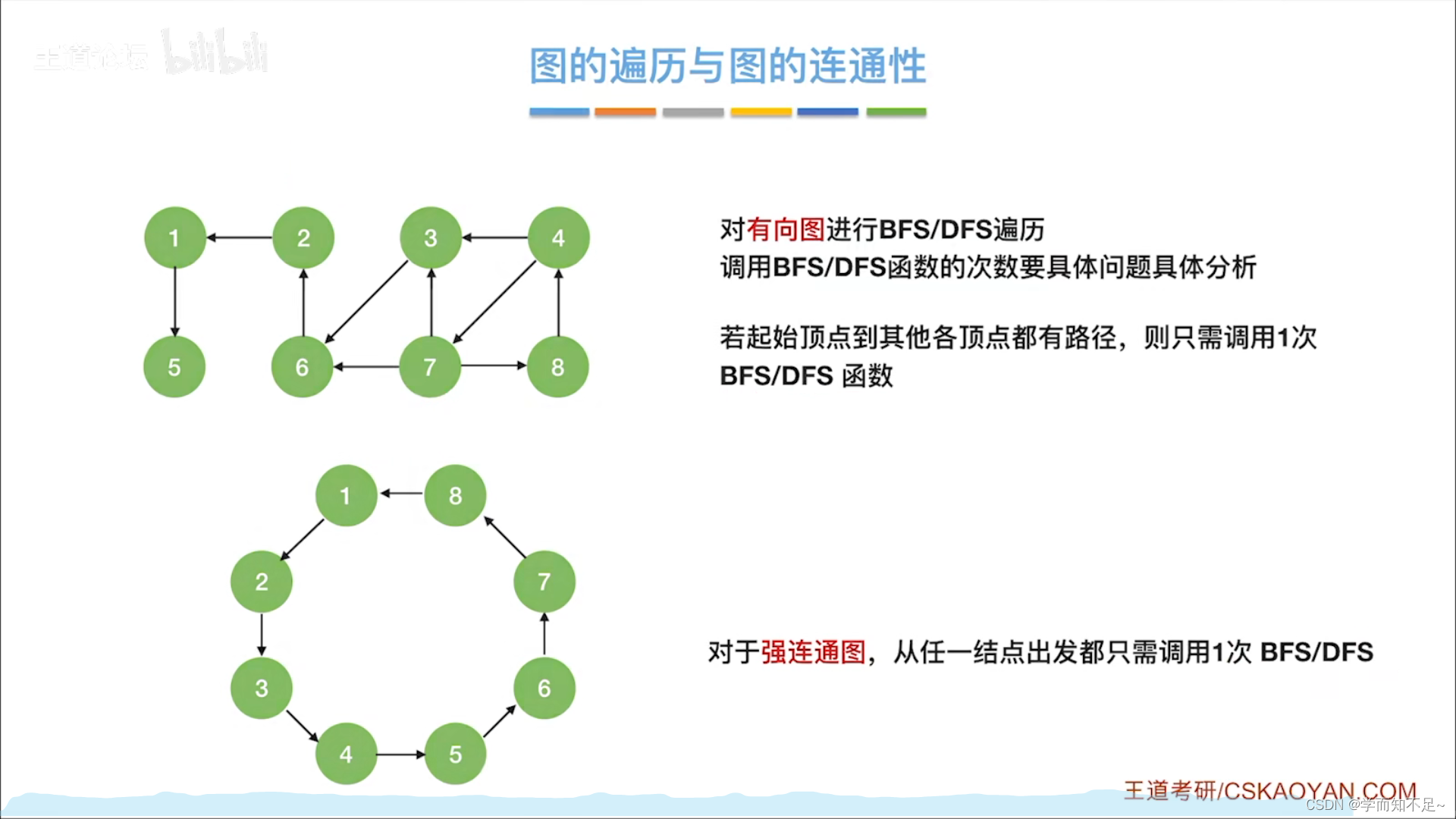
图的遍历和图的连通性
无向图:
有向图:
总结
图的最小生成树(MST)
概念


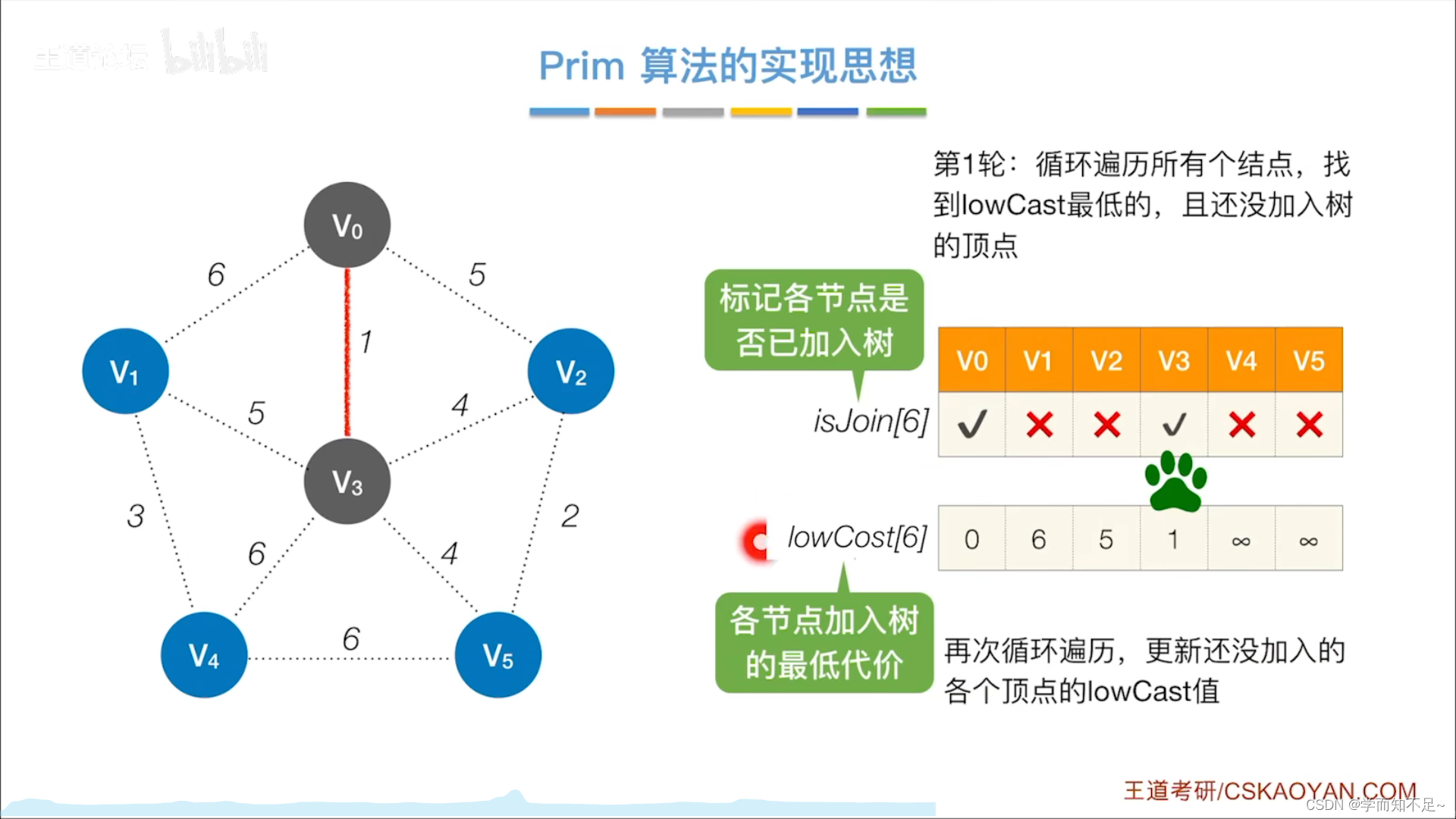
Prim算法(普里姆)

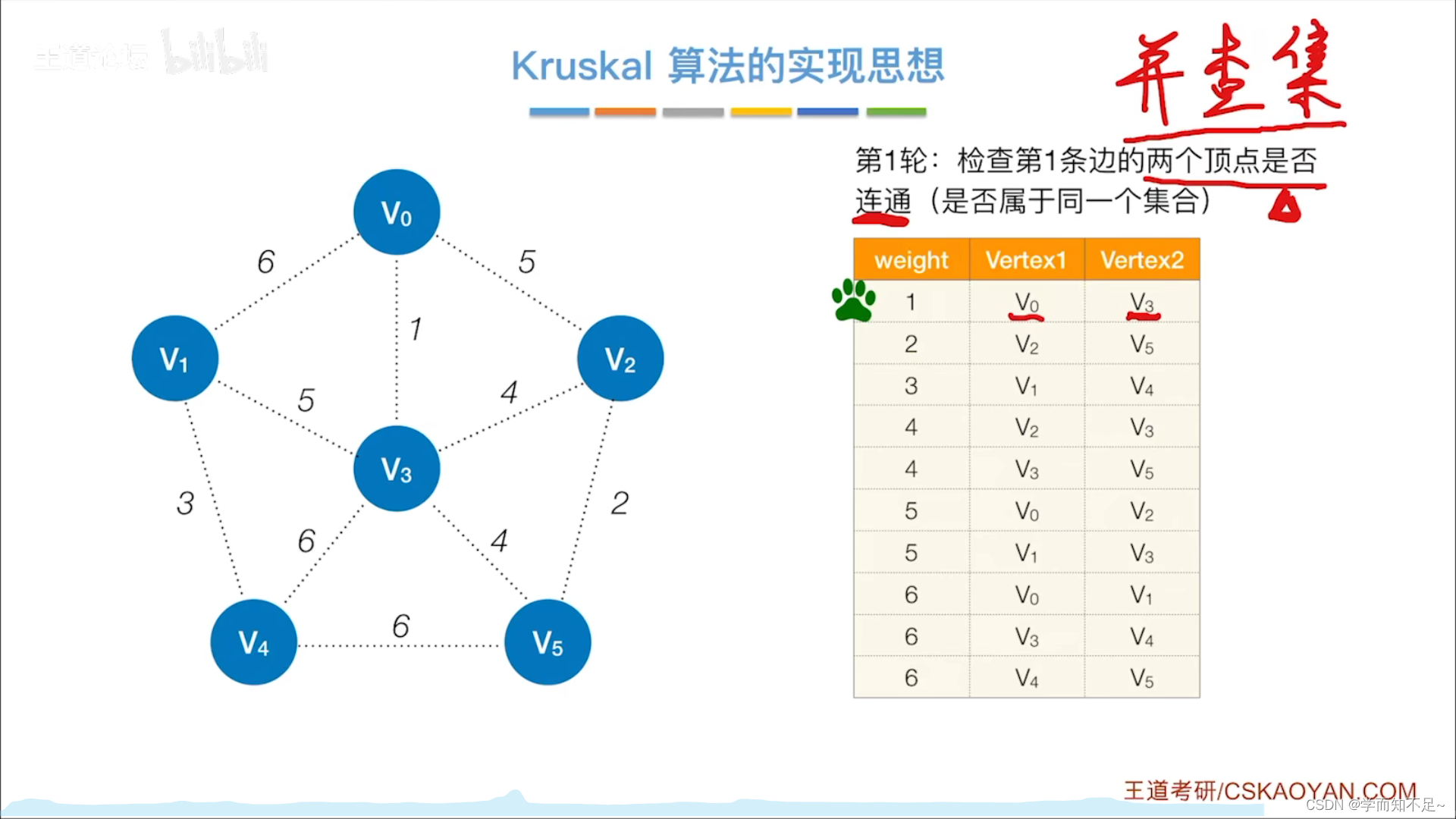
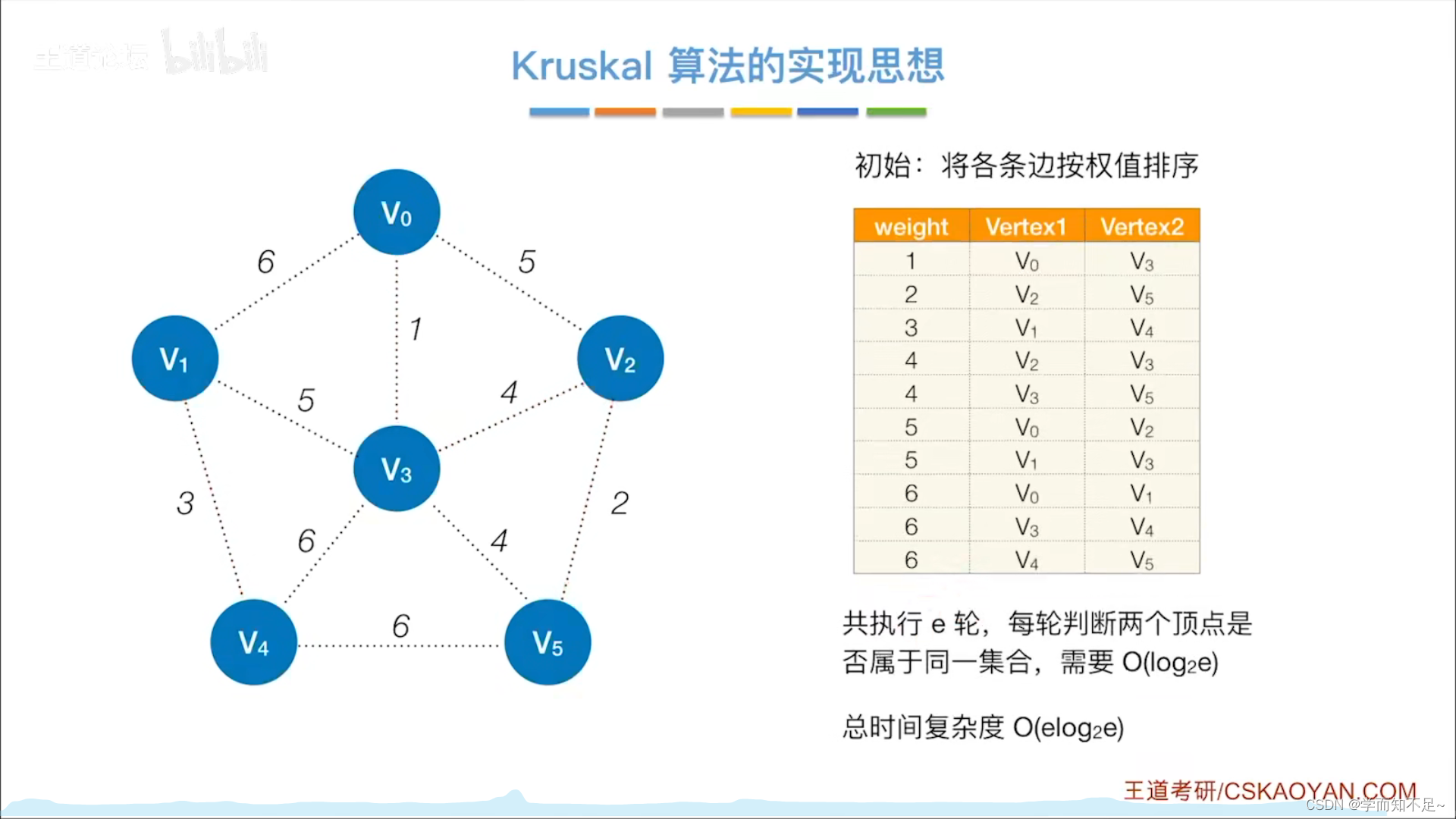
Kruskal算法(克鲁斯卡尔)
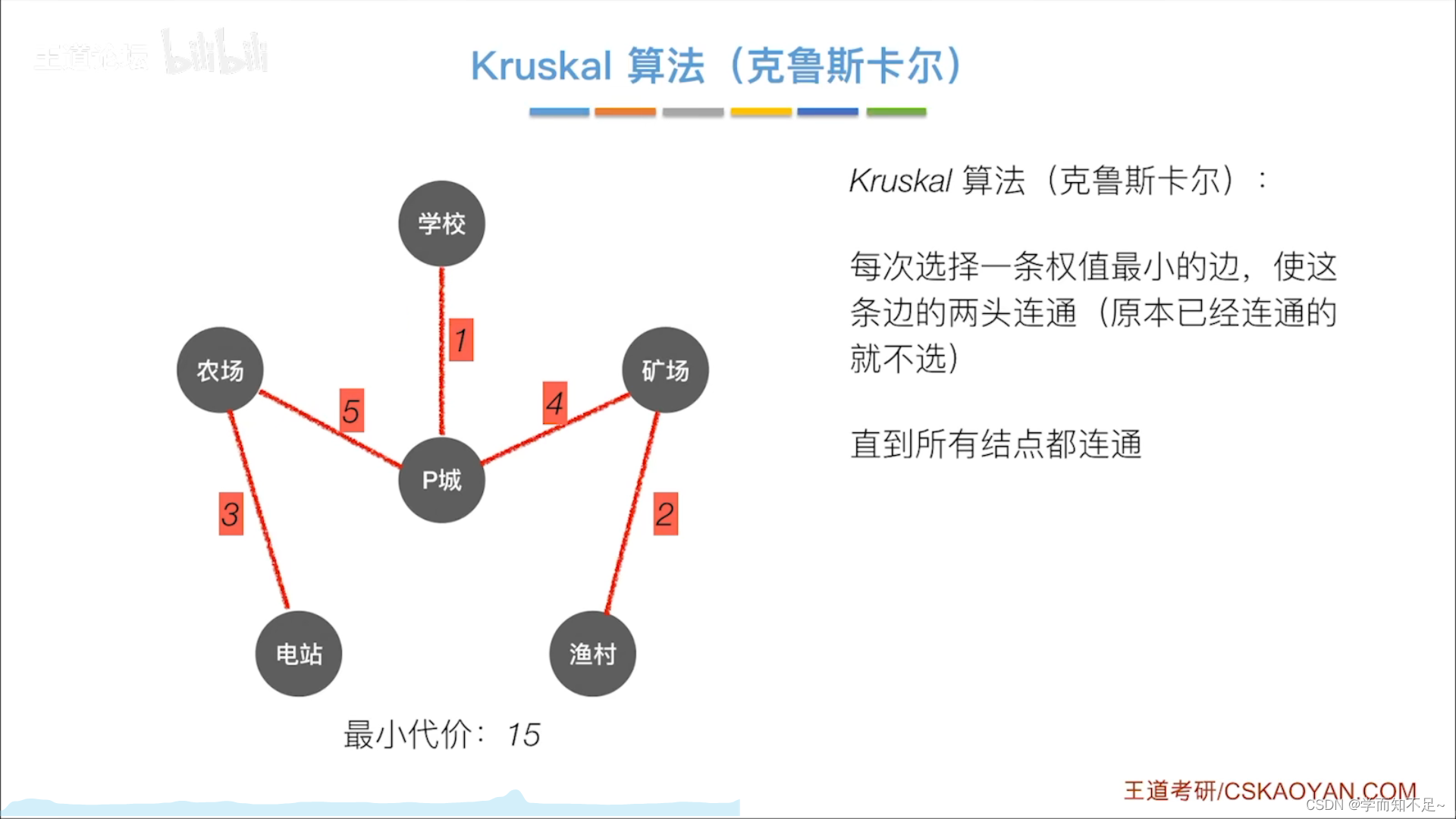
两种算法对比

Prim算法的实现思想
Kruskal算法的实现思想
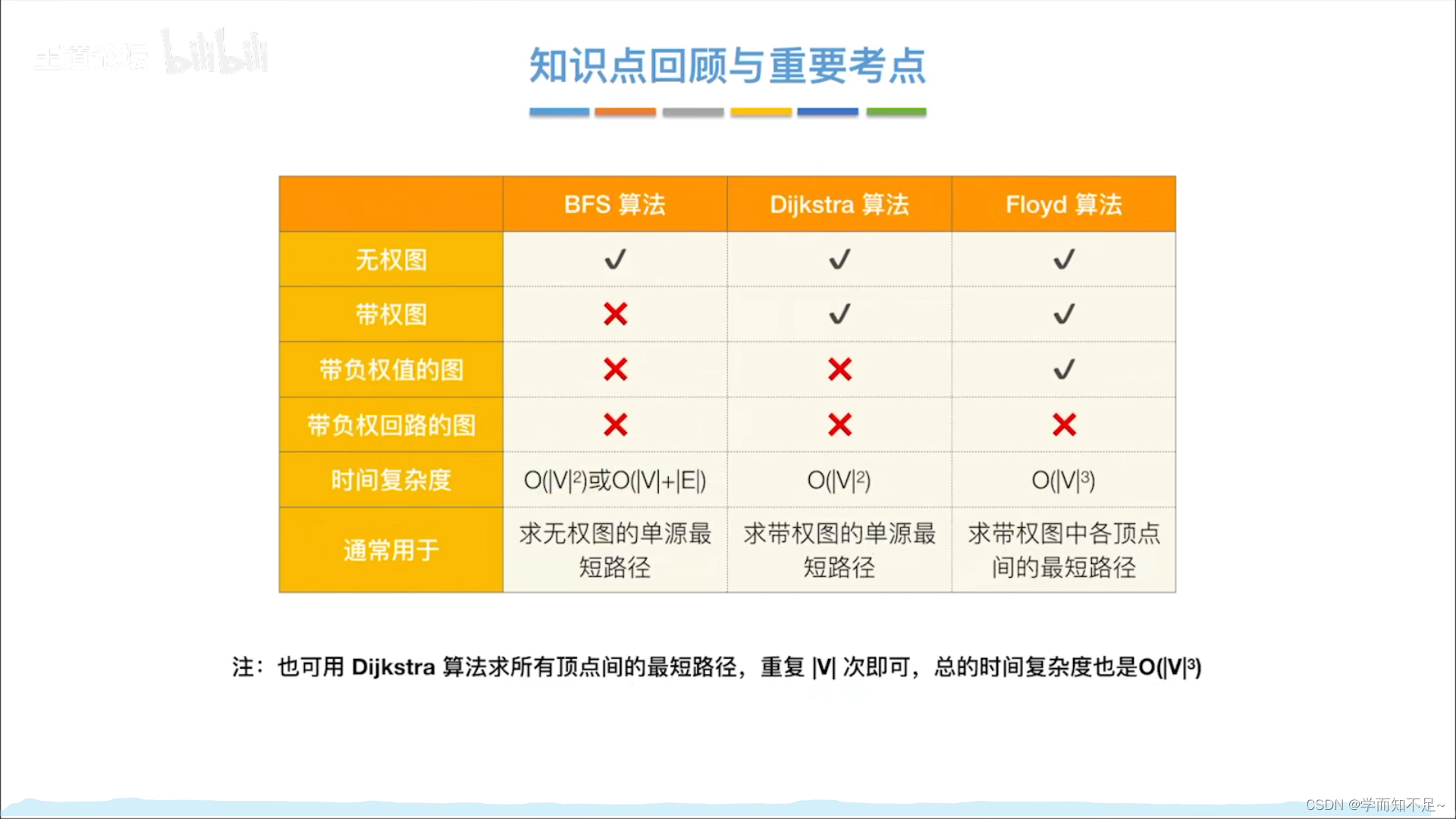
图的最短路径问题
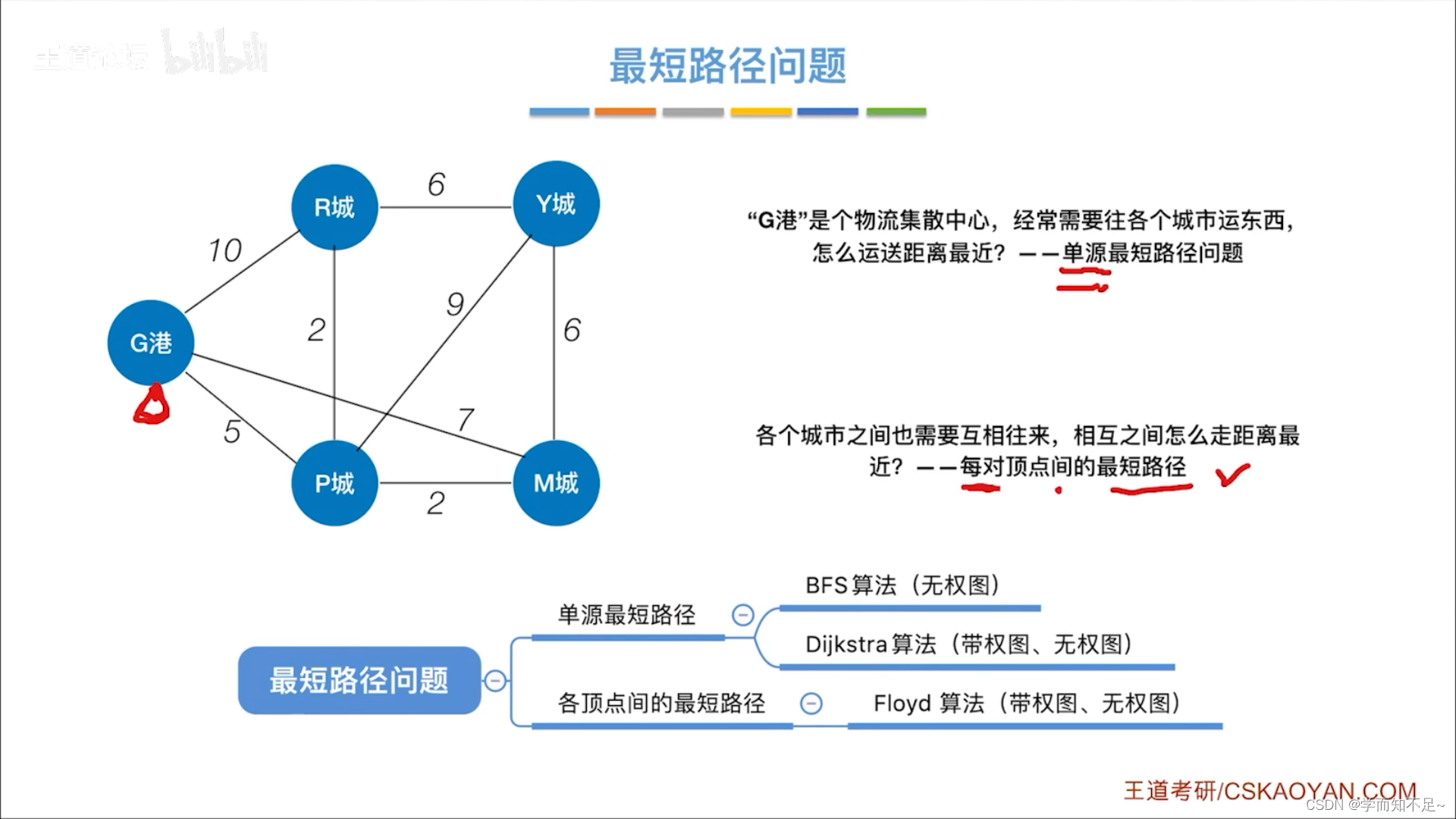
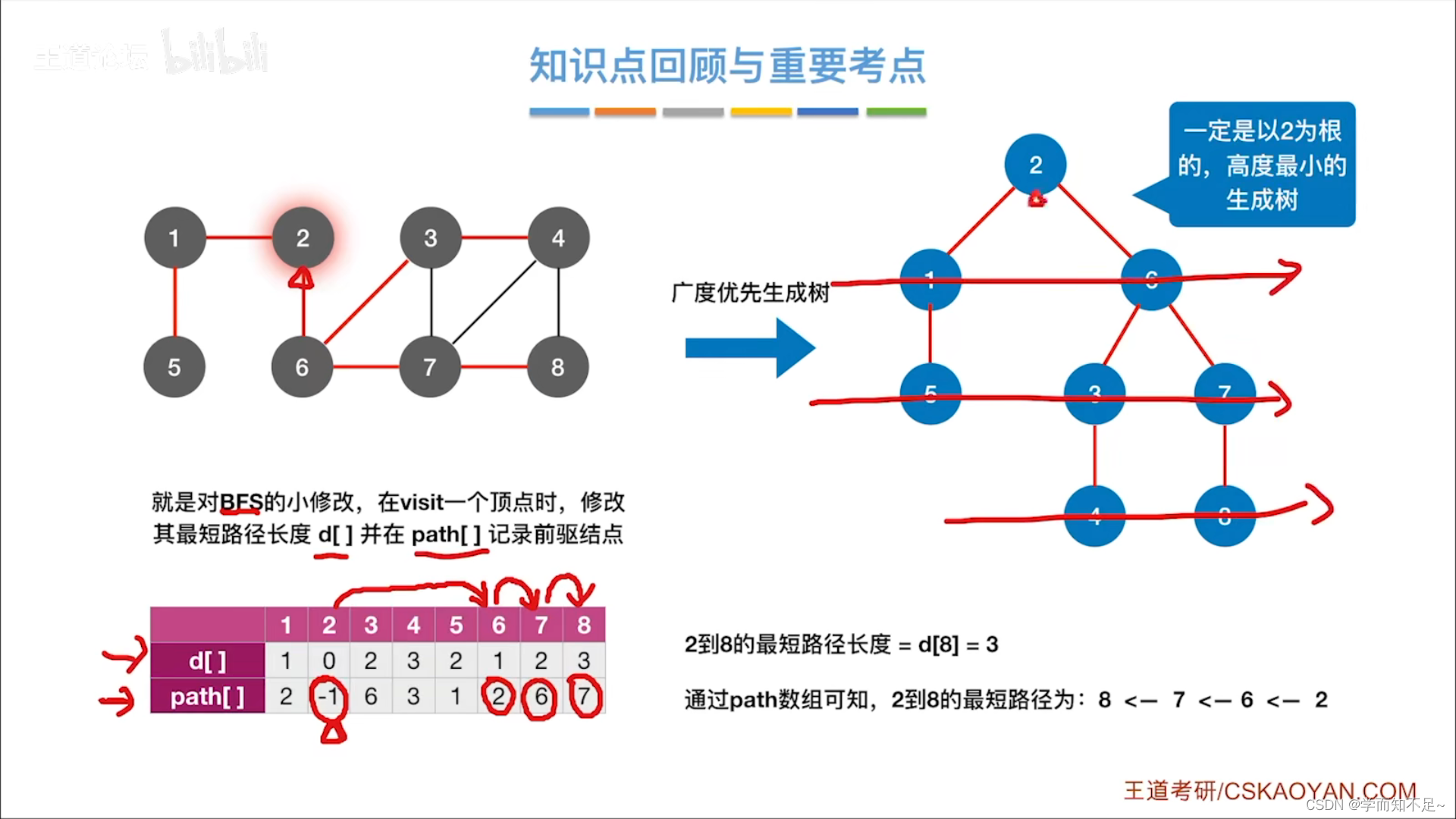
BFS求无权图的单源最短路径
BFS实际上的结果就是单源最短路径
缺点:只能用于不带权的图
代码实现

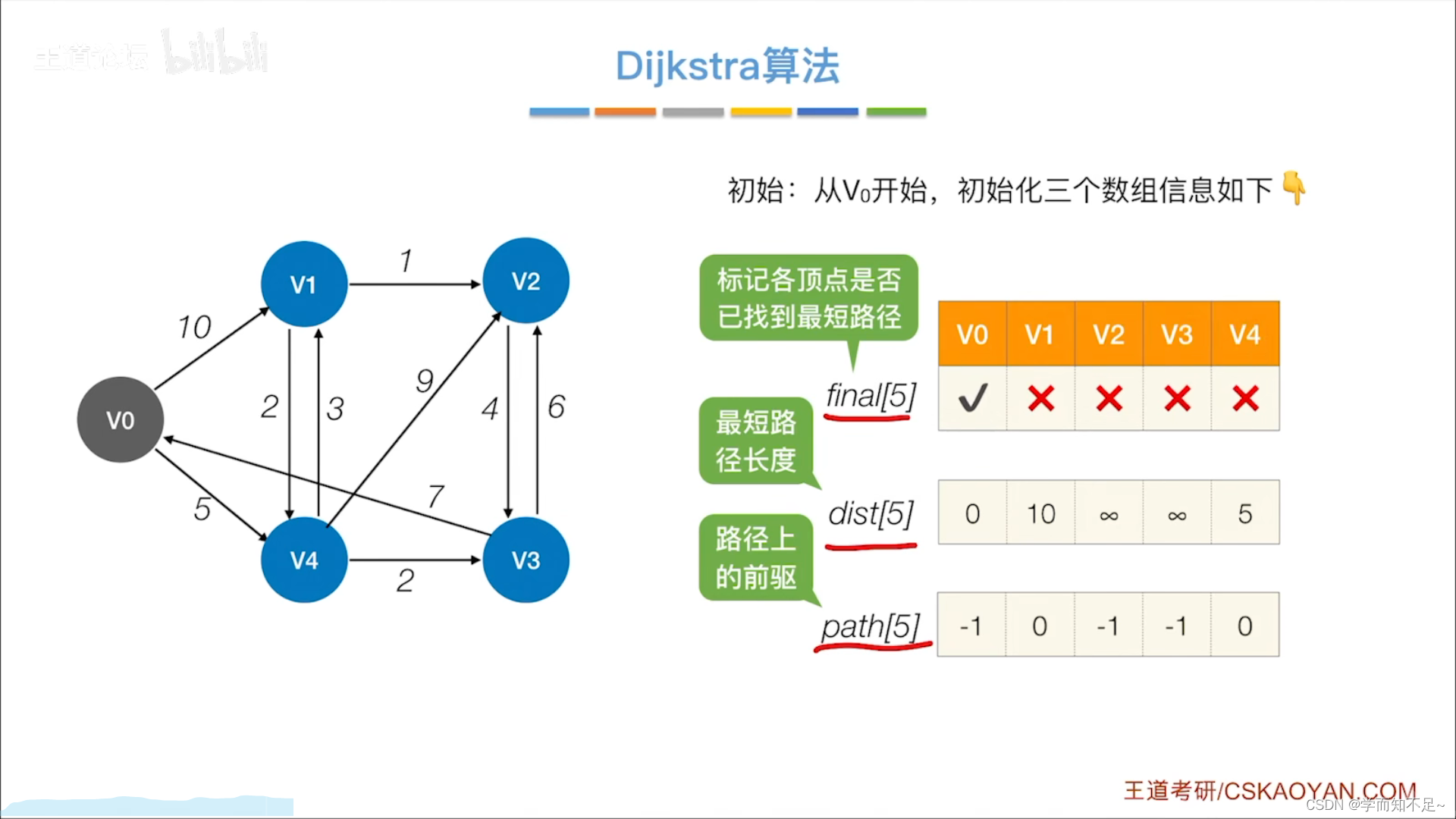
Dijkstra(迪杰斯特拉)算法

步骤
- 初始:
- 第一轮:
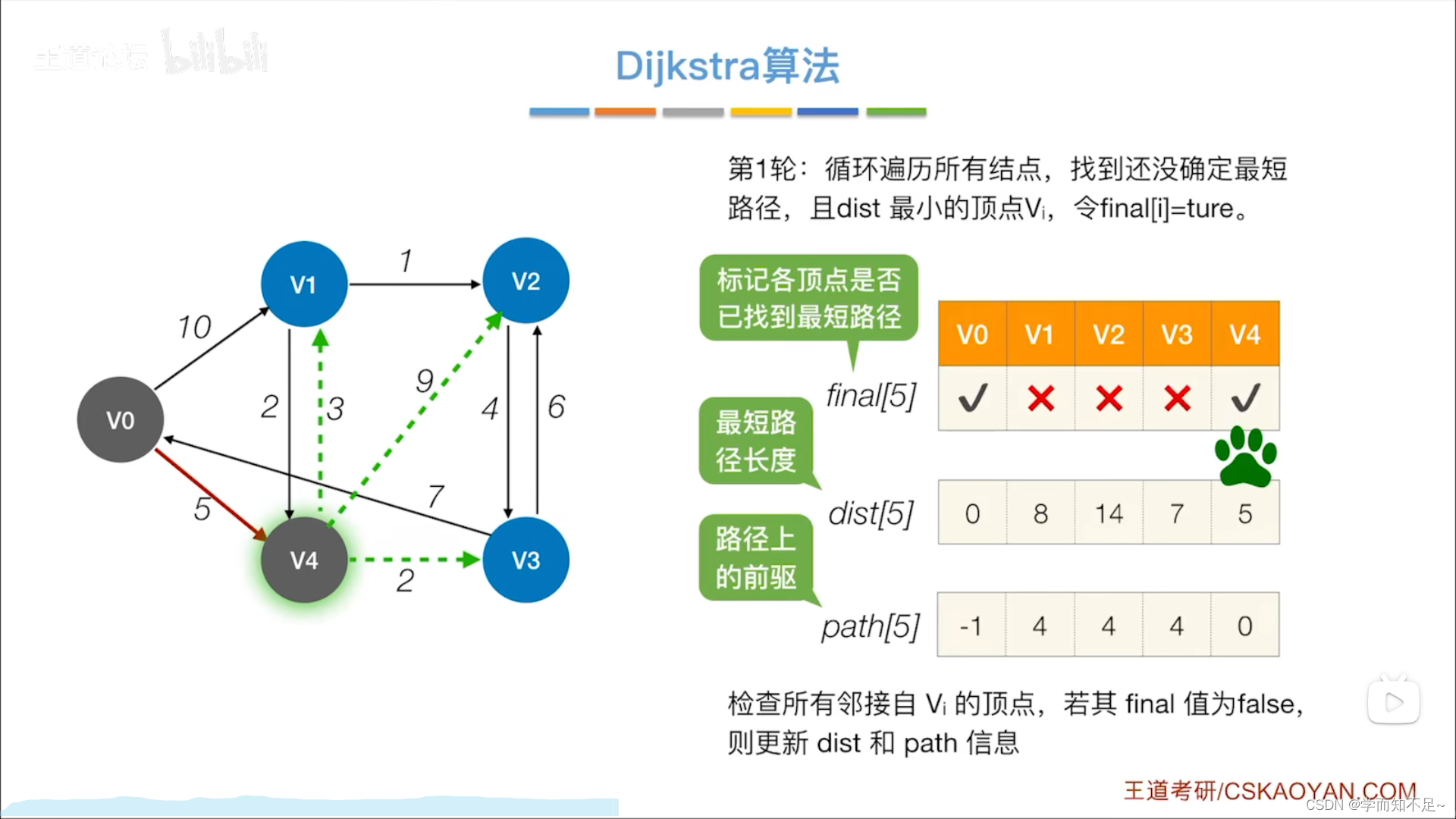
- 第二轮:
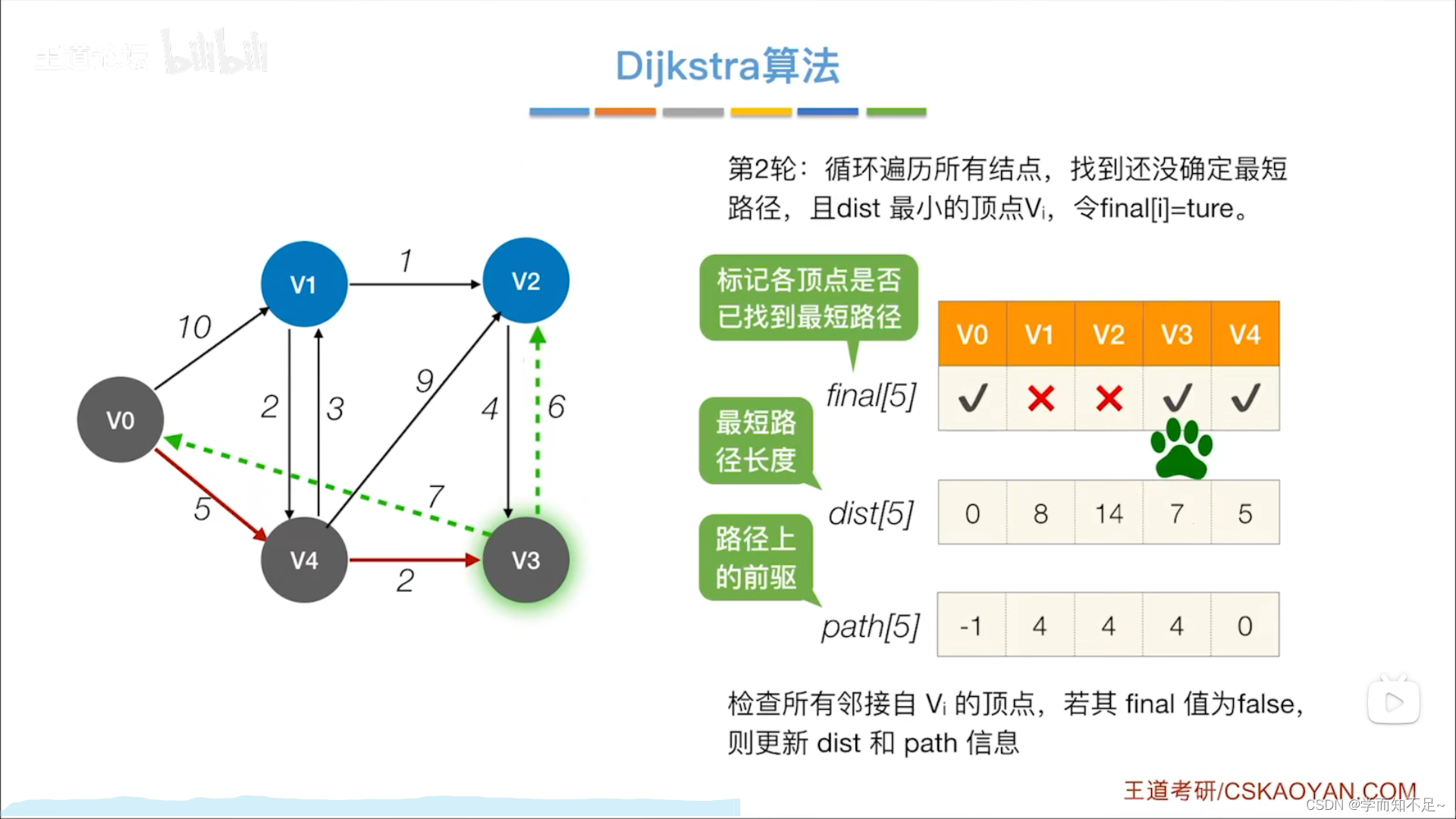
- 第三轮:
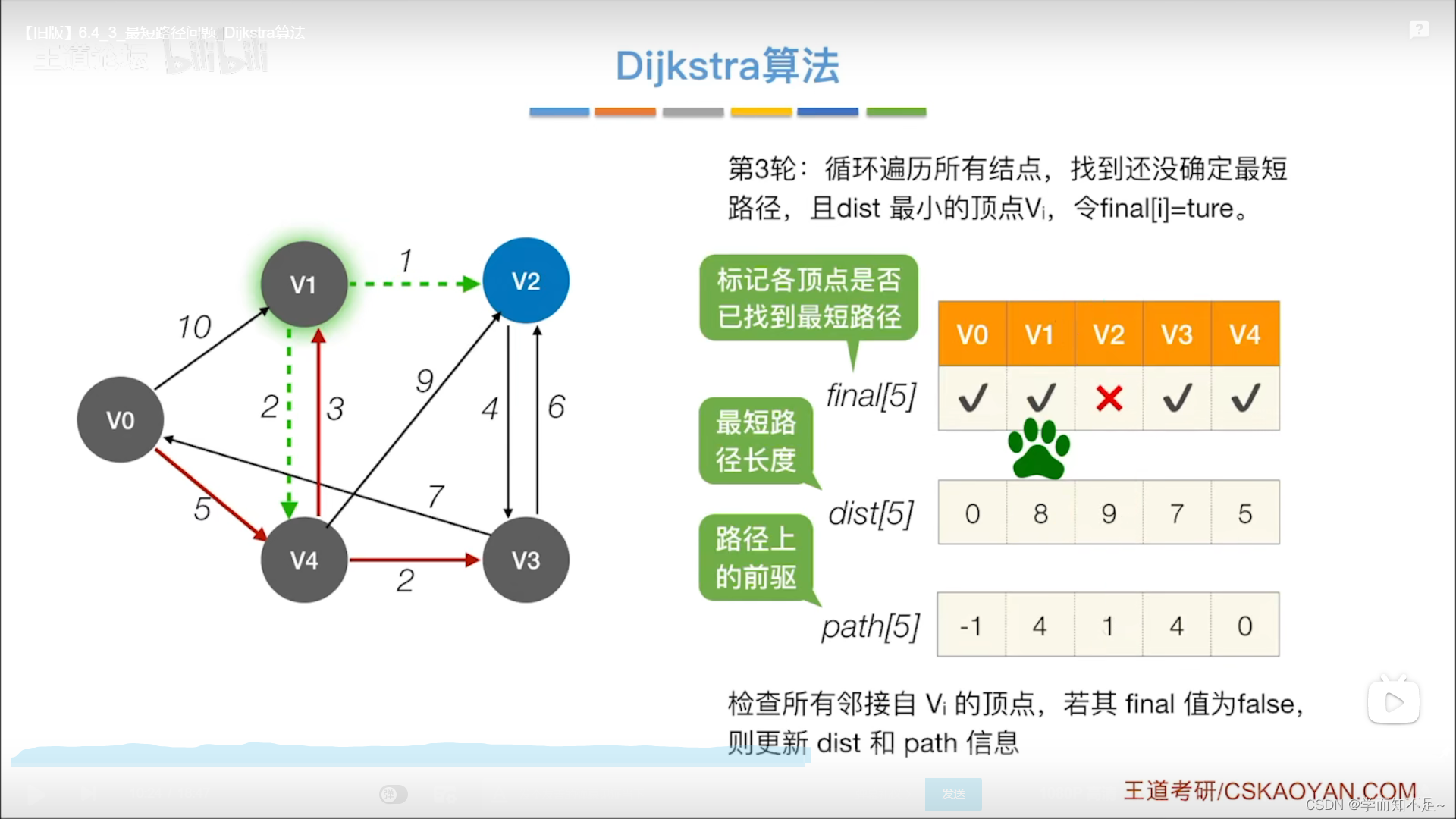
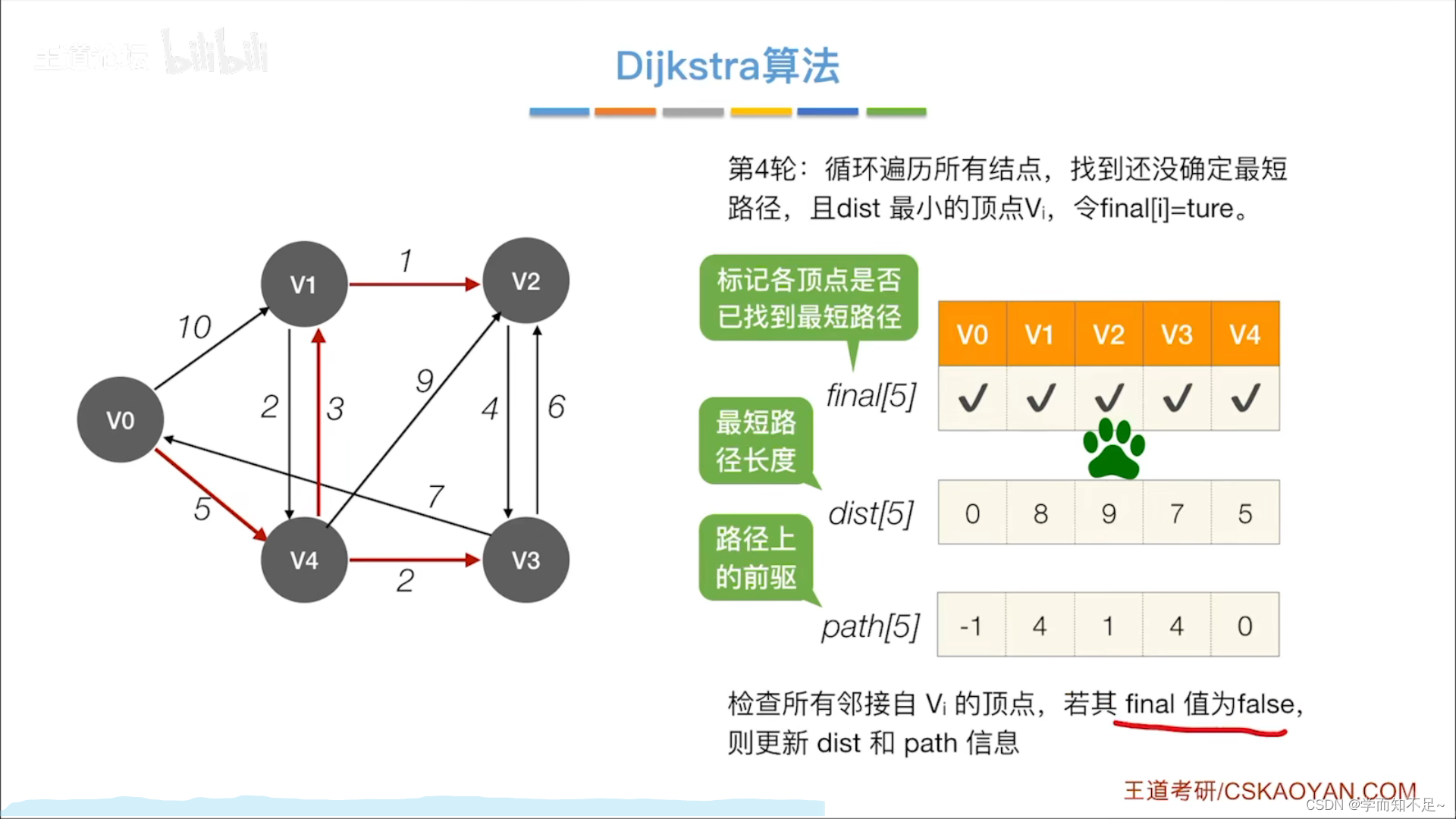
- 第四轮:
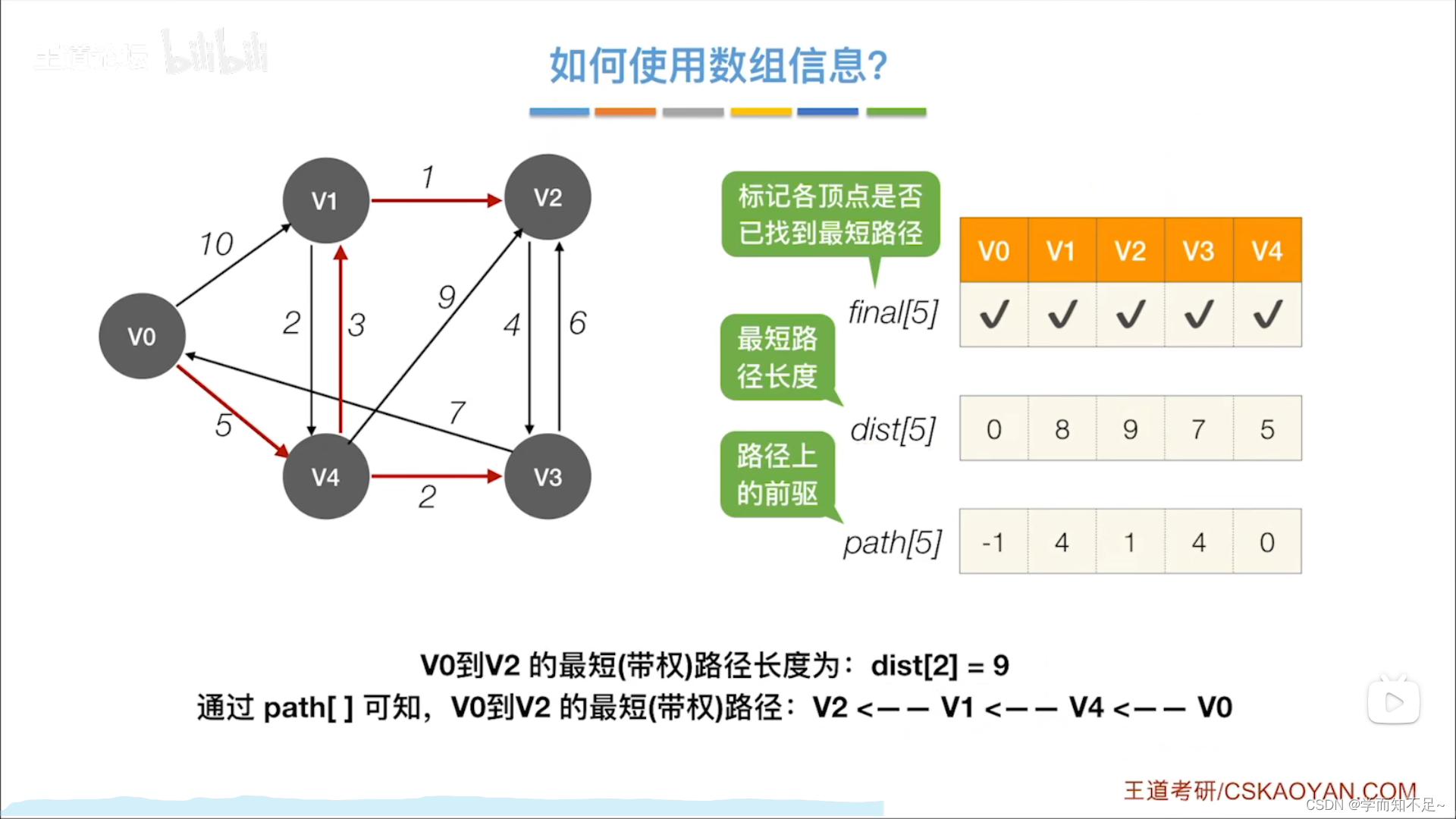
如何使用数组信息
时间复杂度
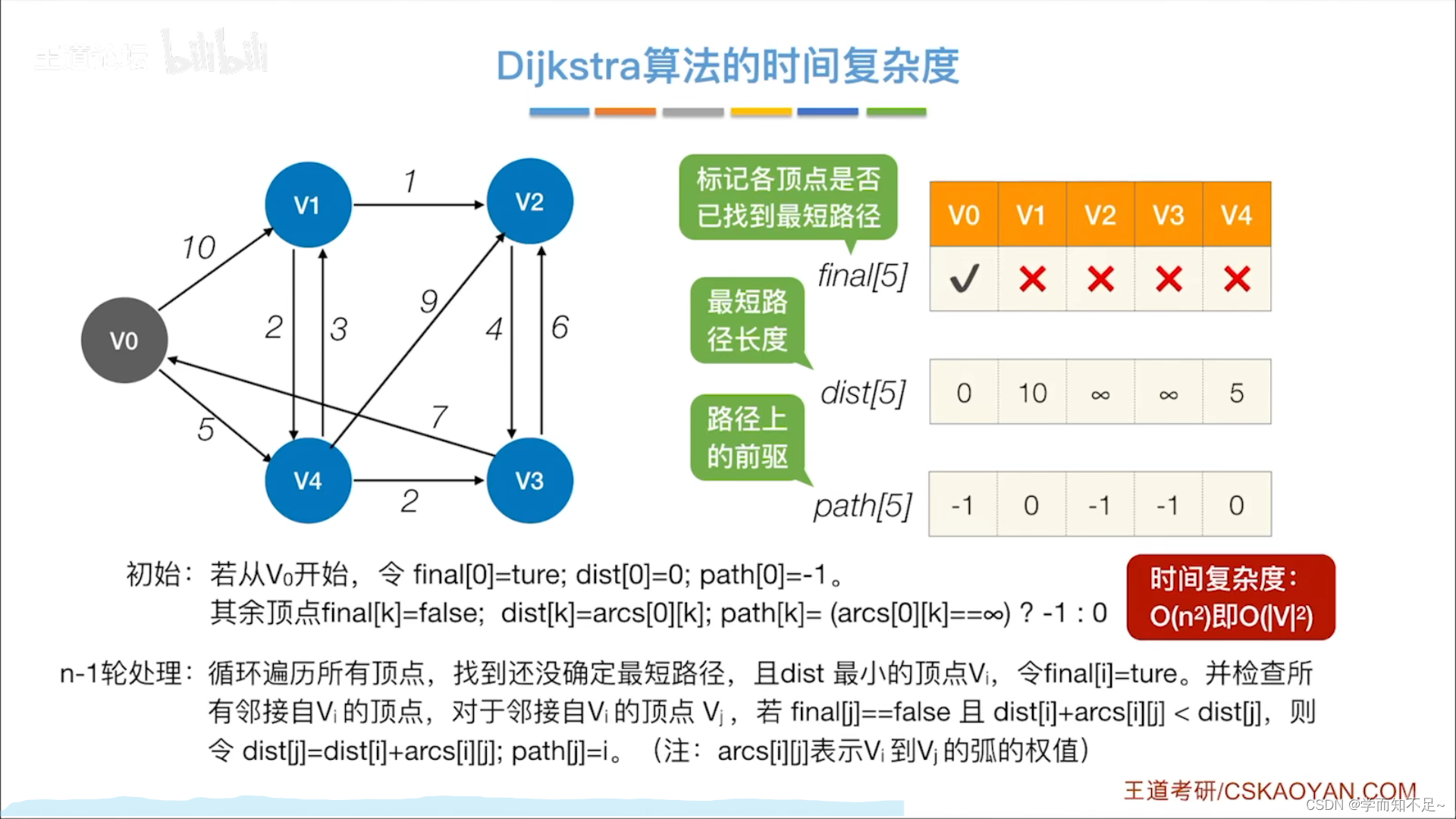
对比Prim算法的实现思想
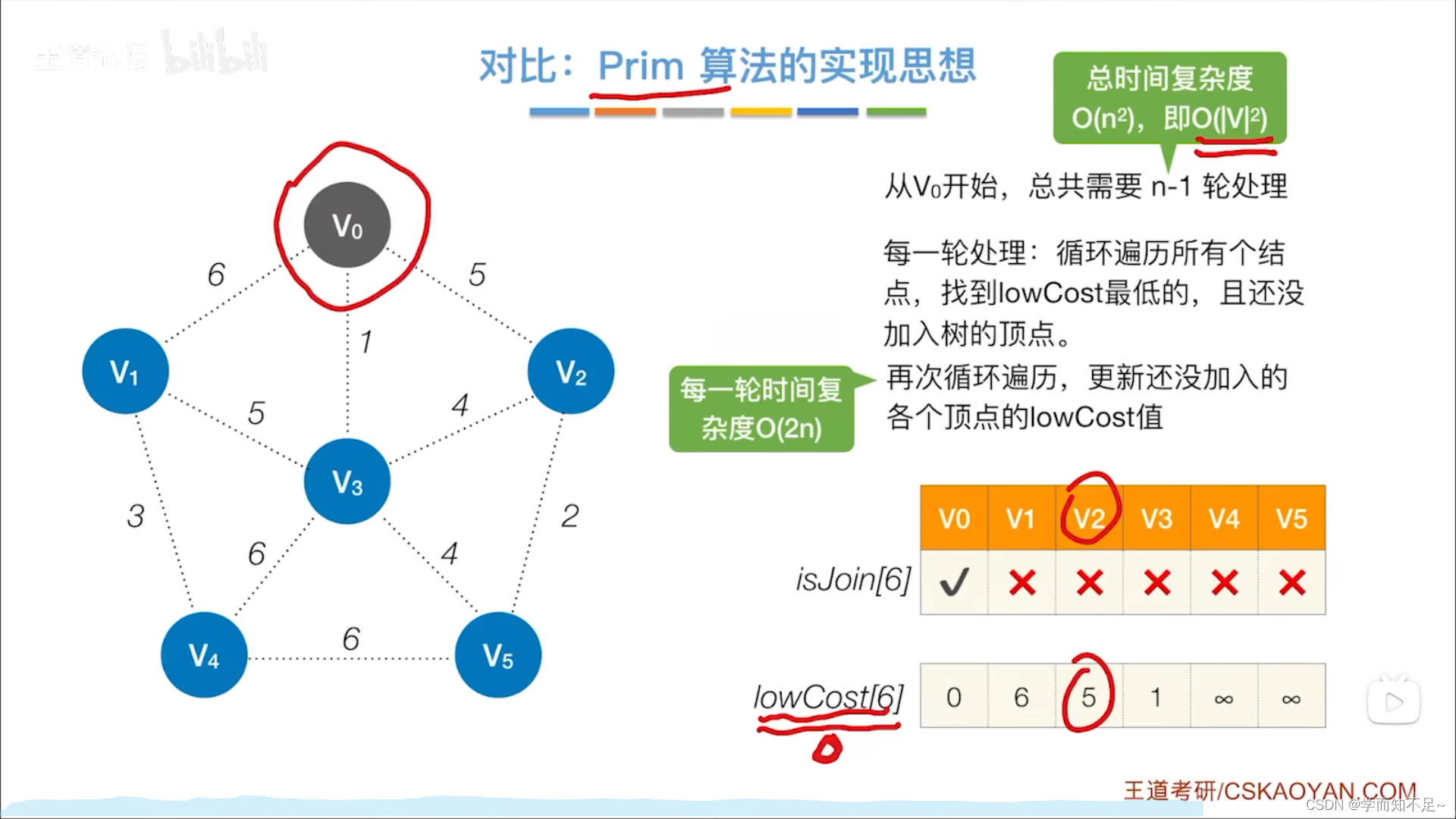
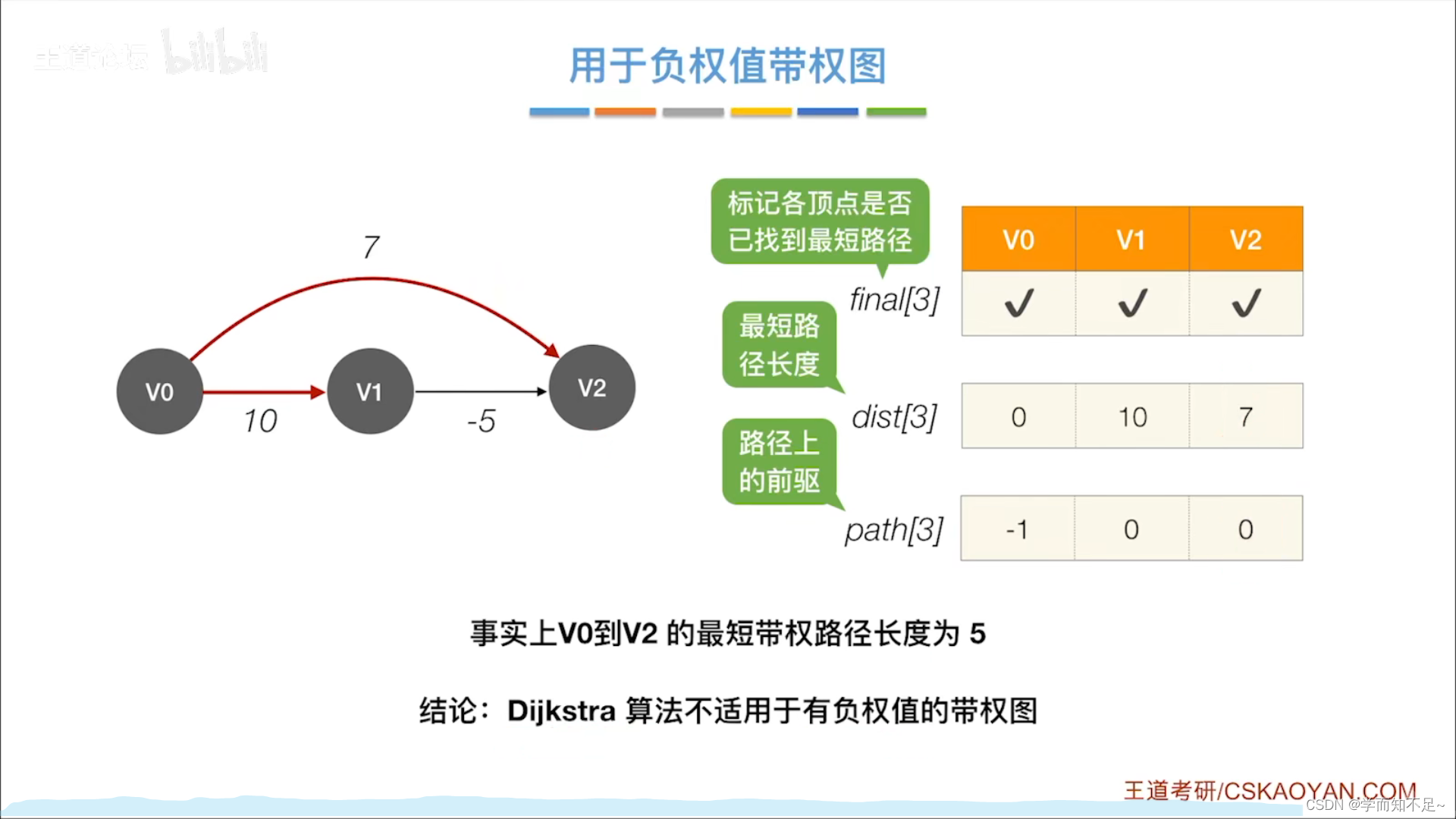
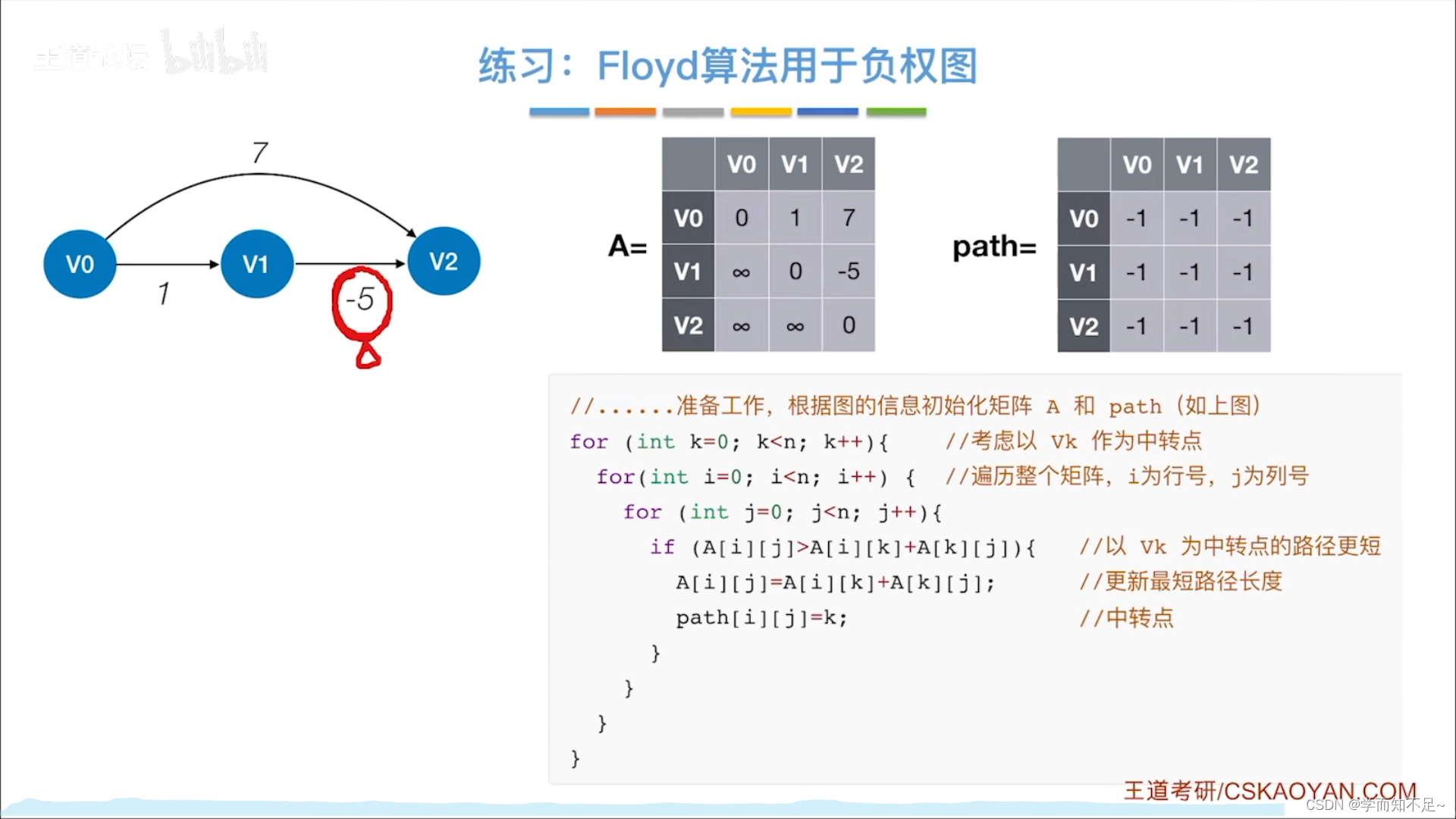
用于负权值带权图
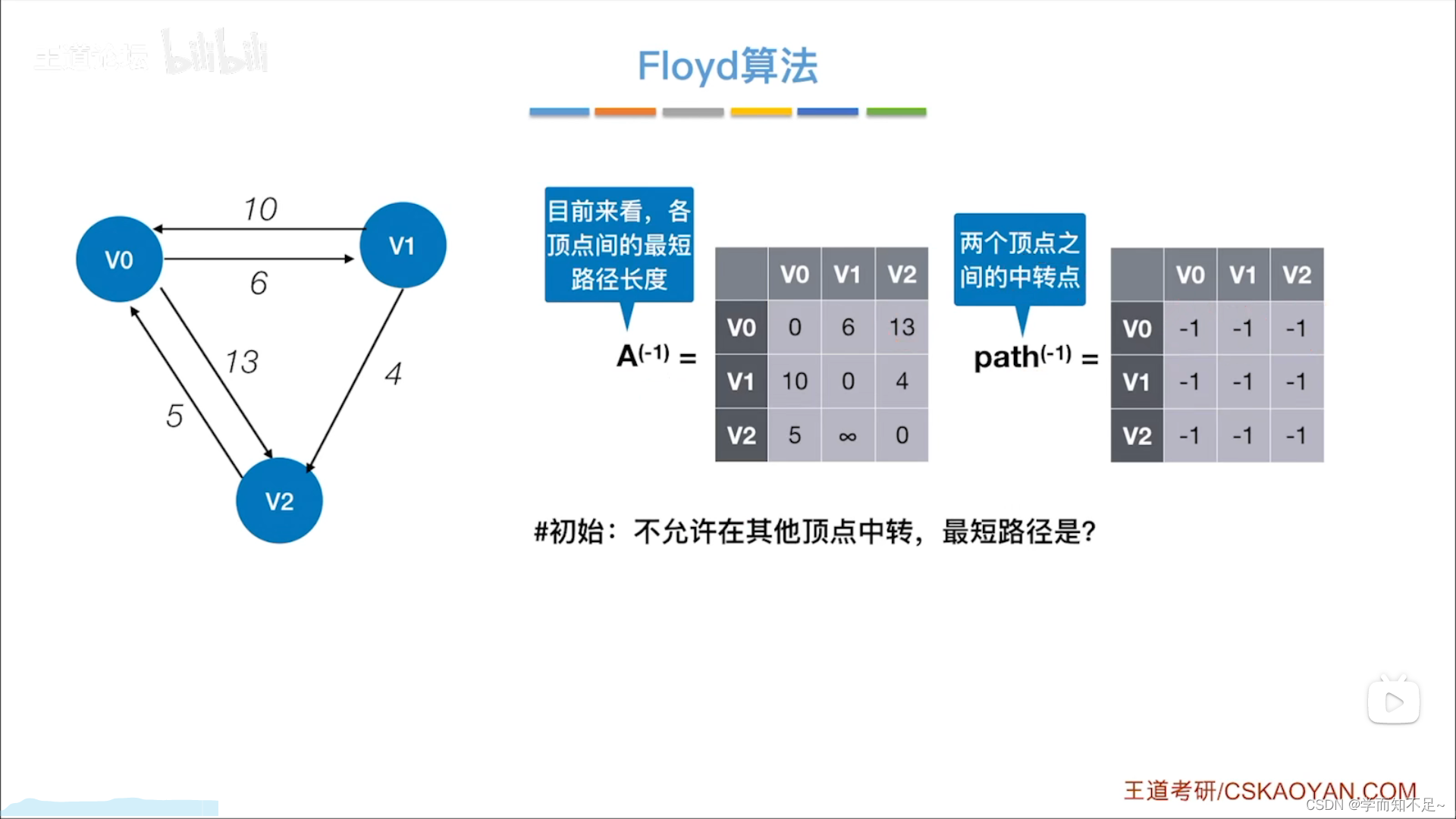
Floyd算法


步骤
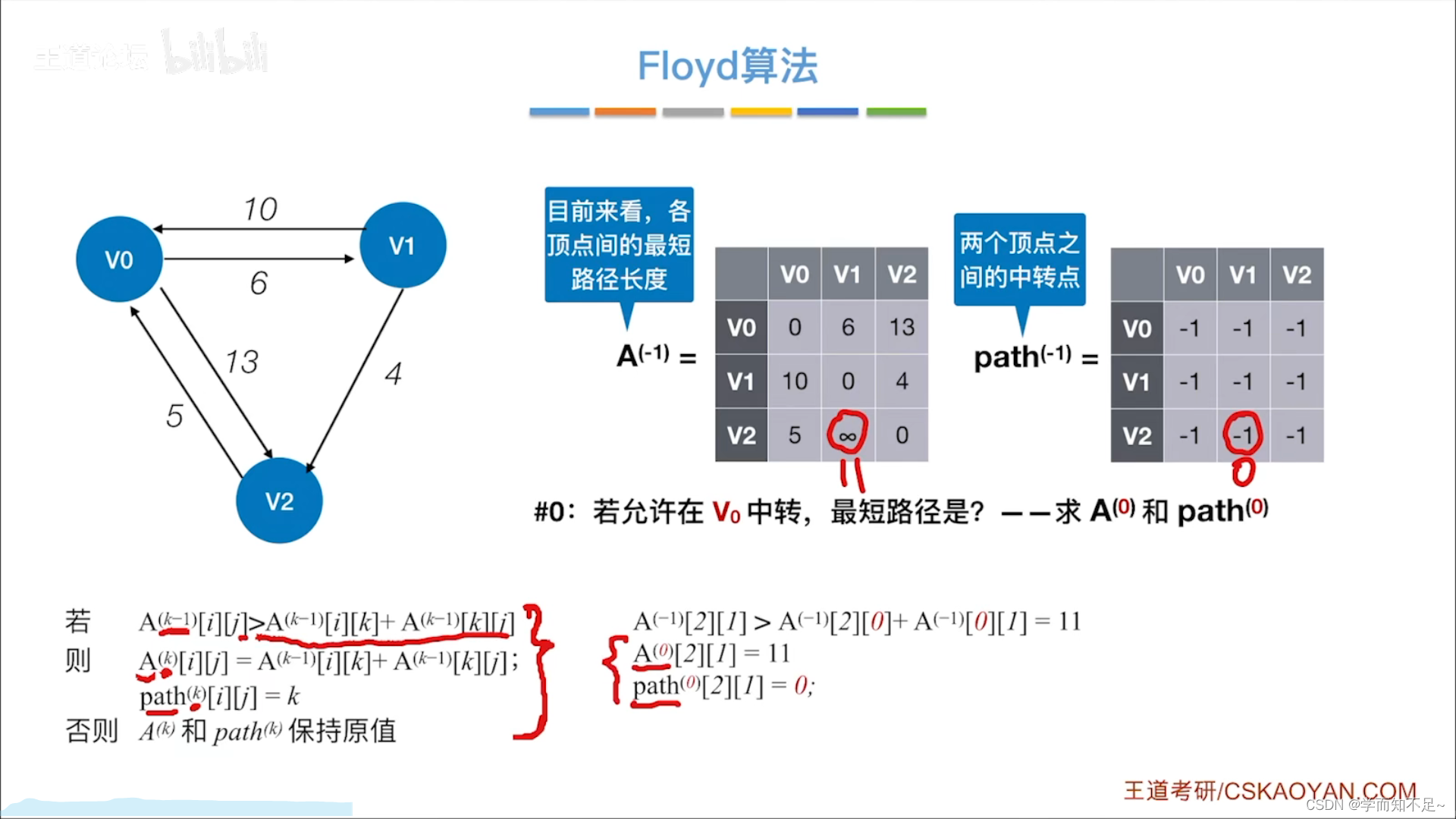

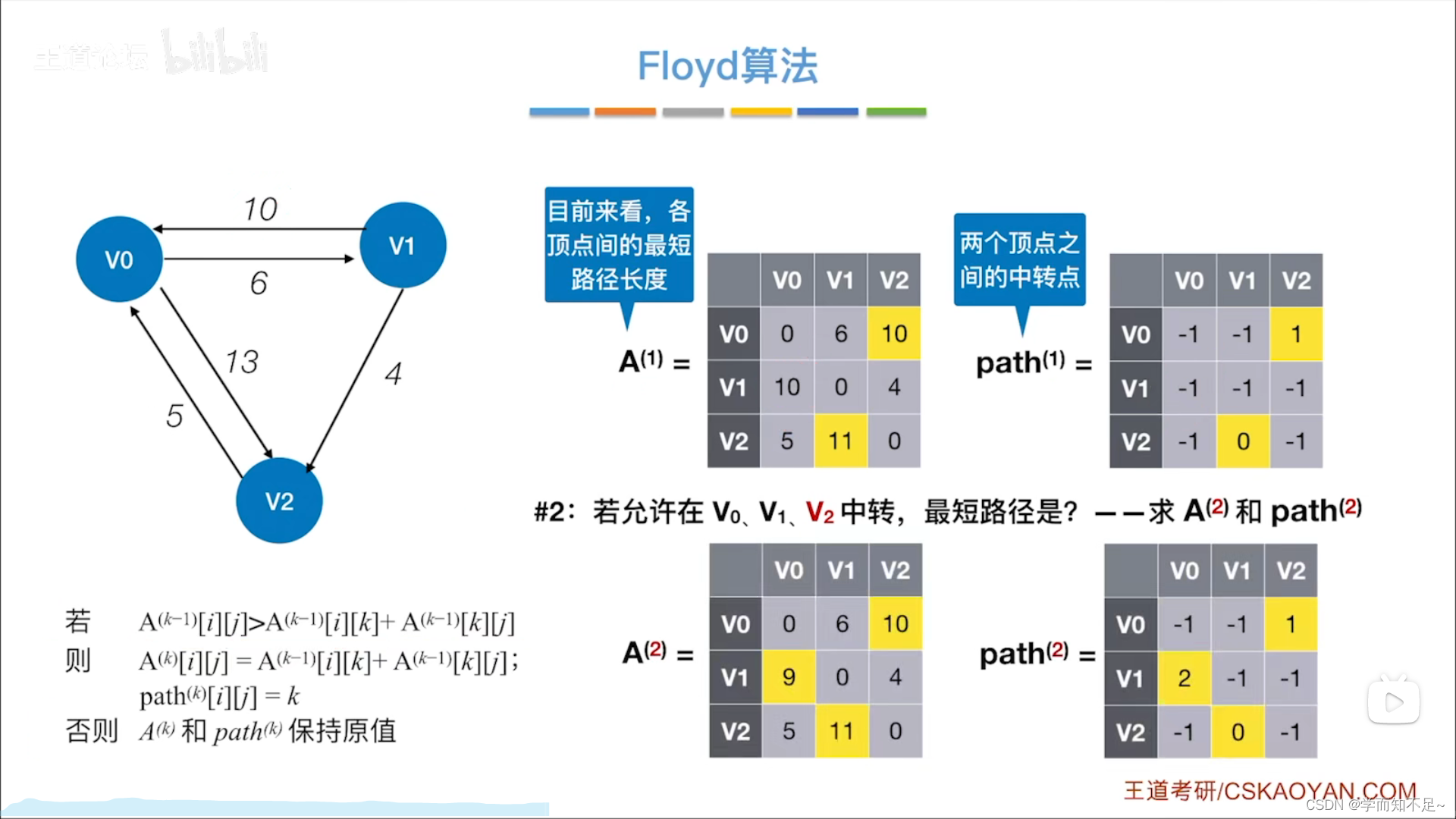
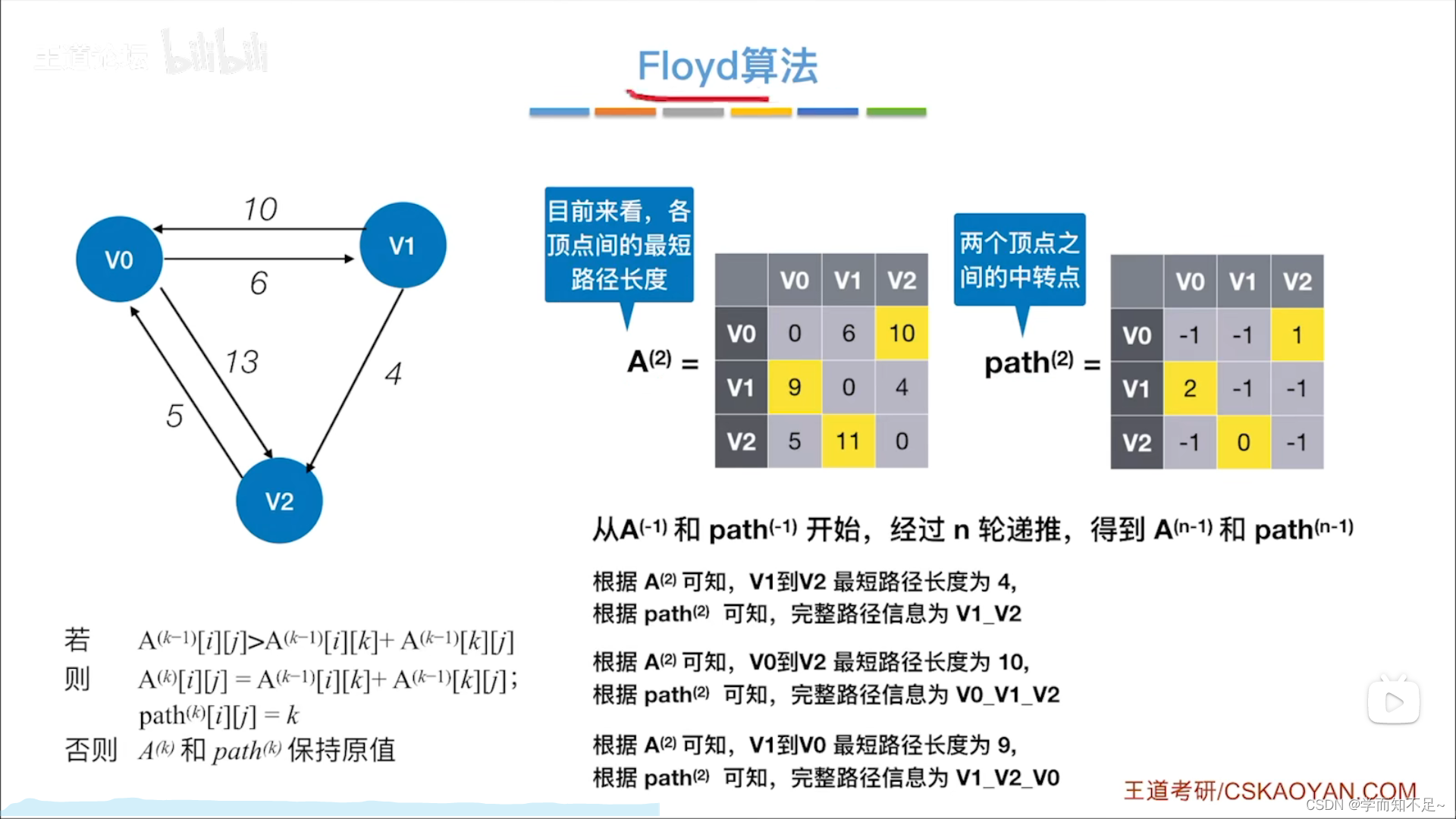
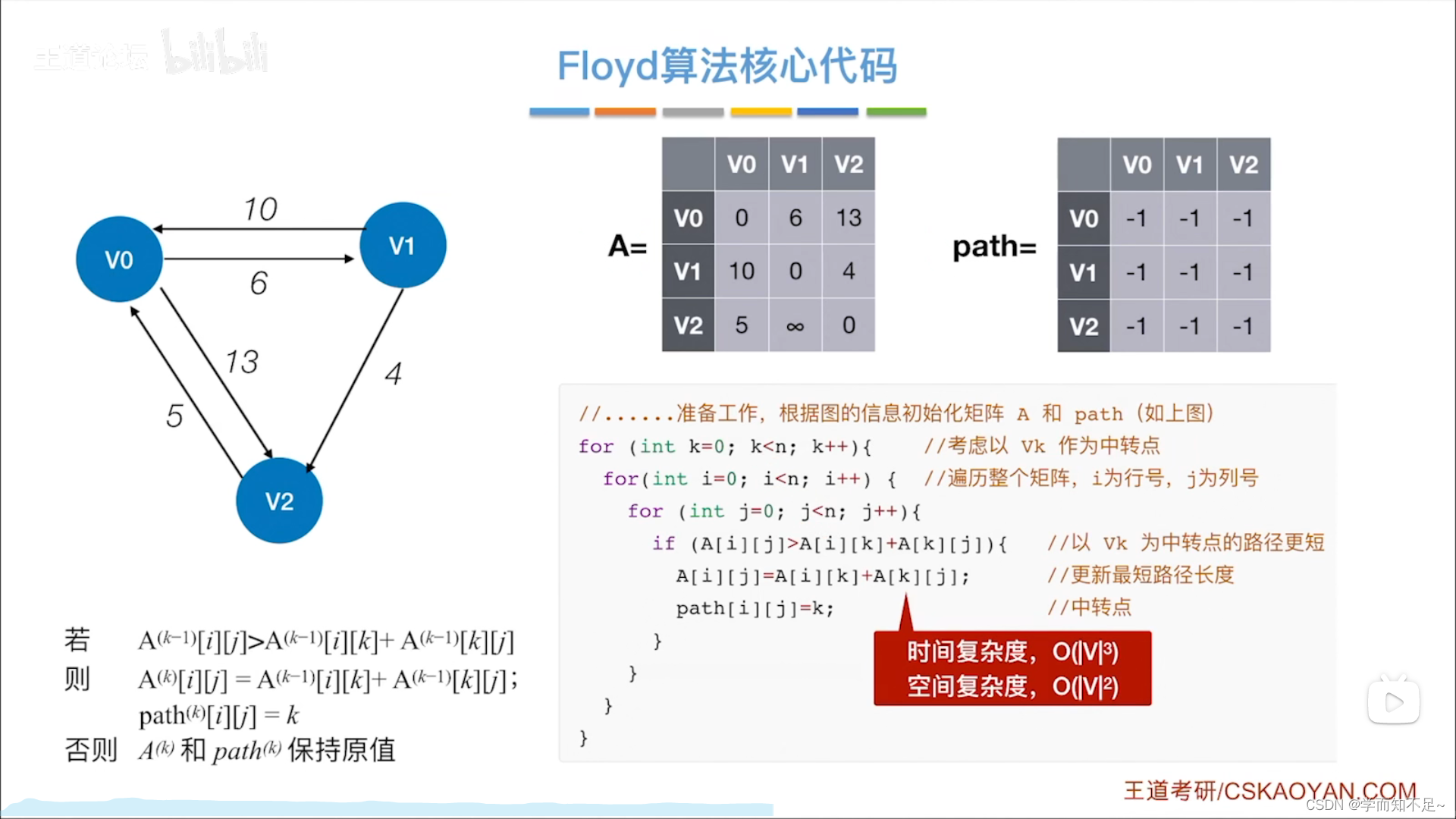
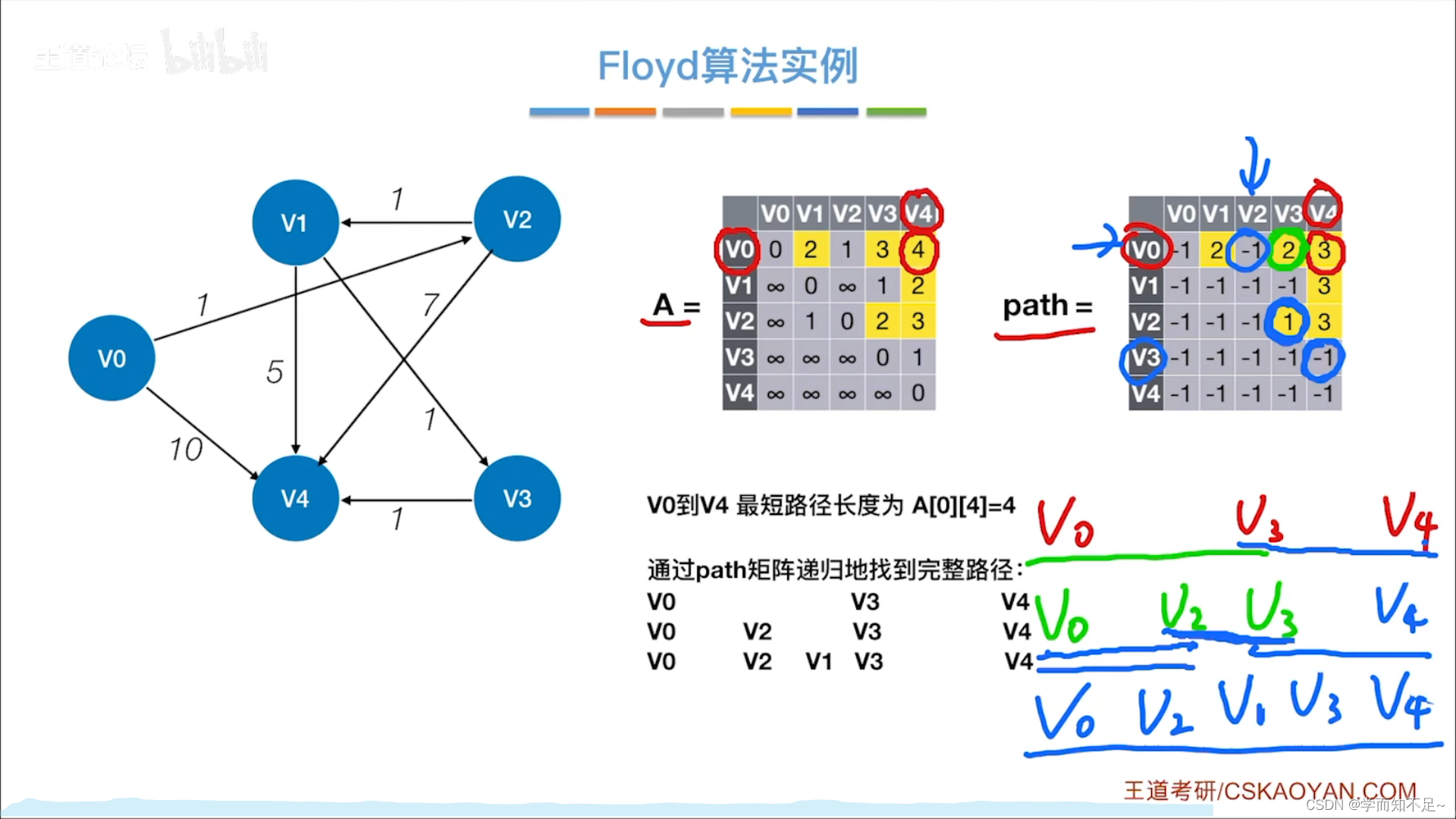
练习
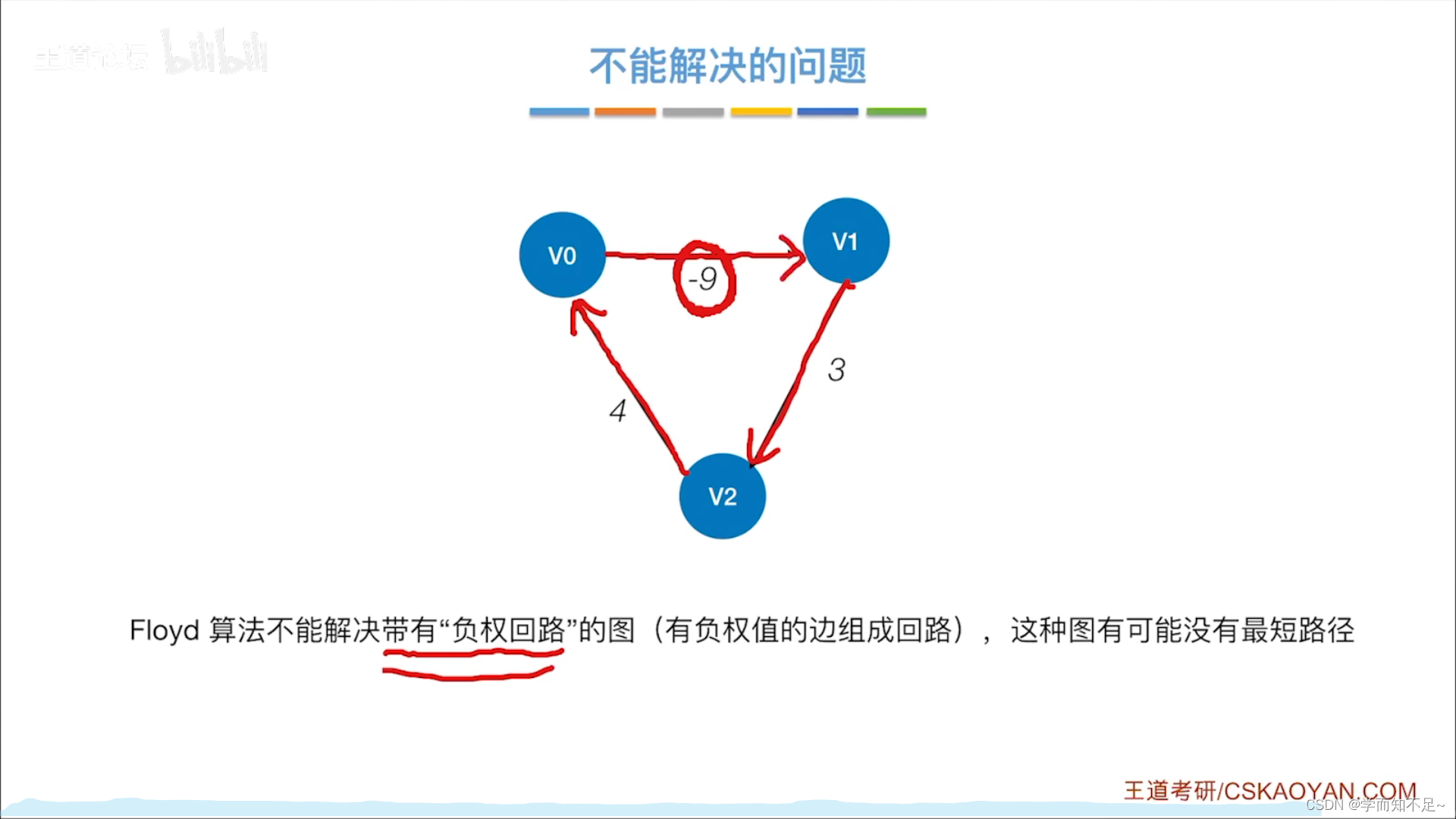
不能解决的问题
总结
有向无环图描述表达式

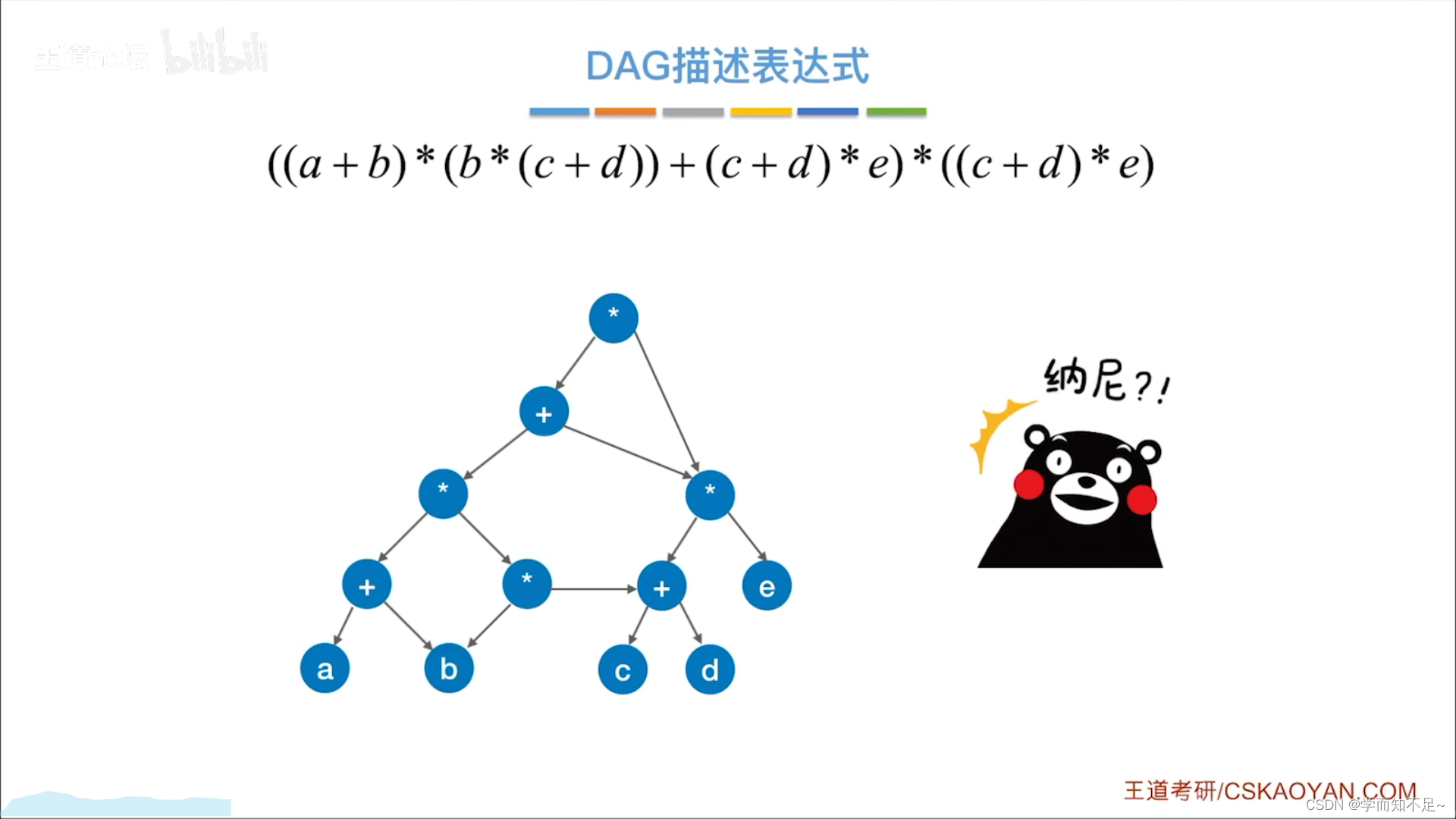
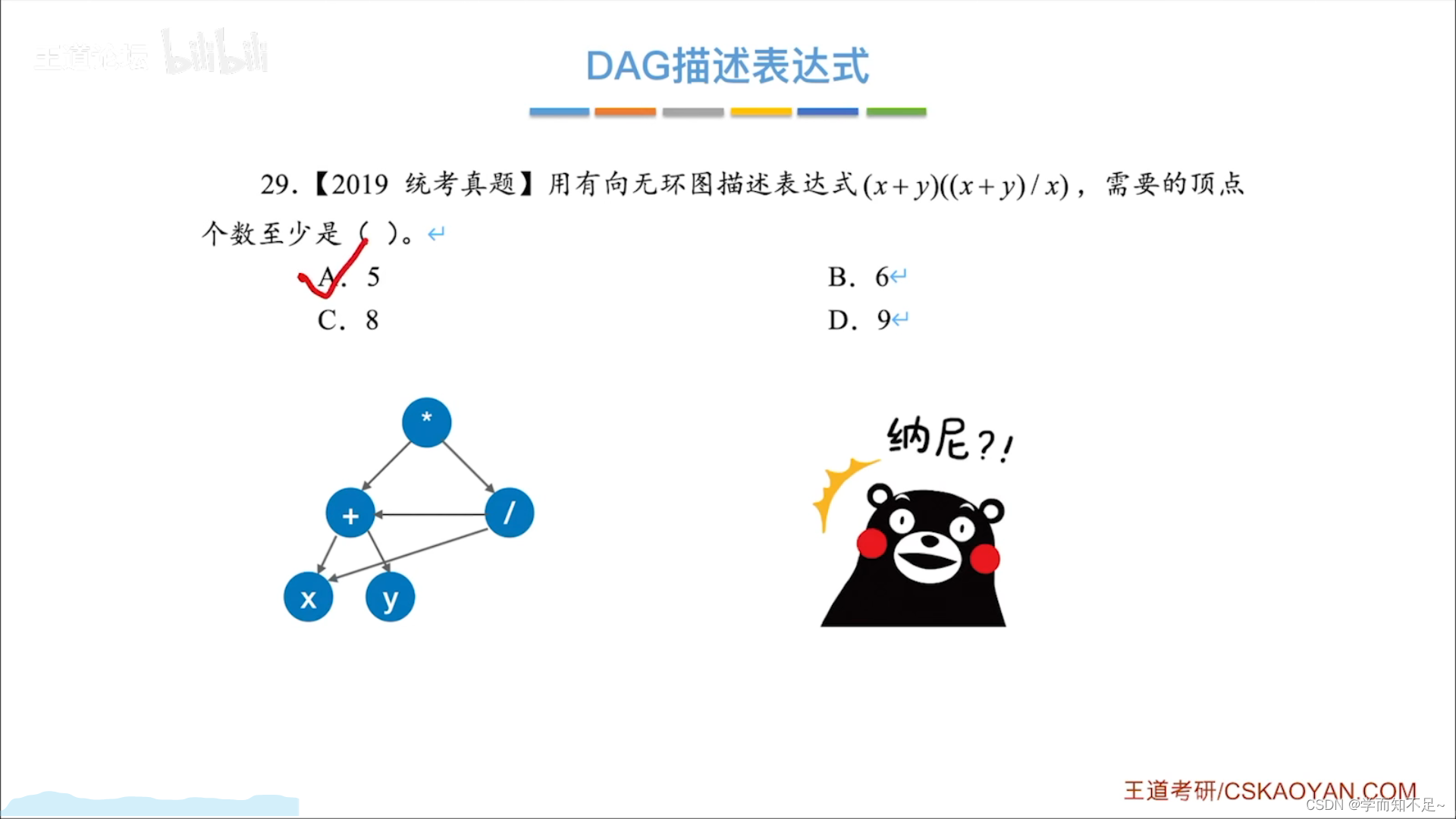
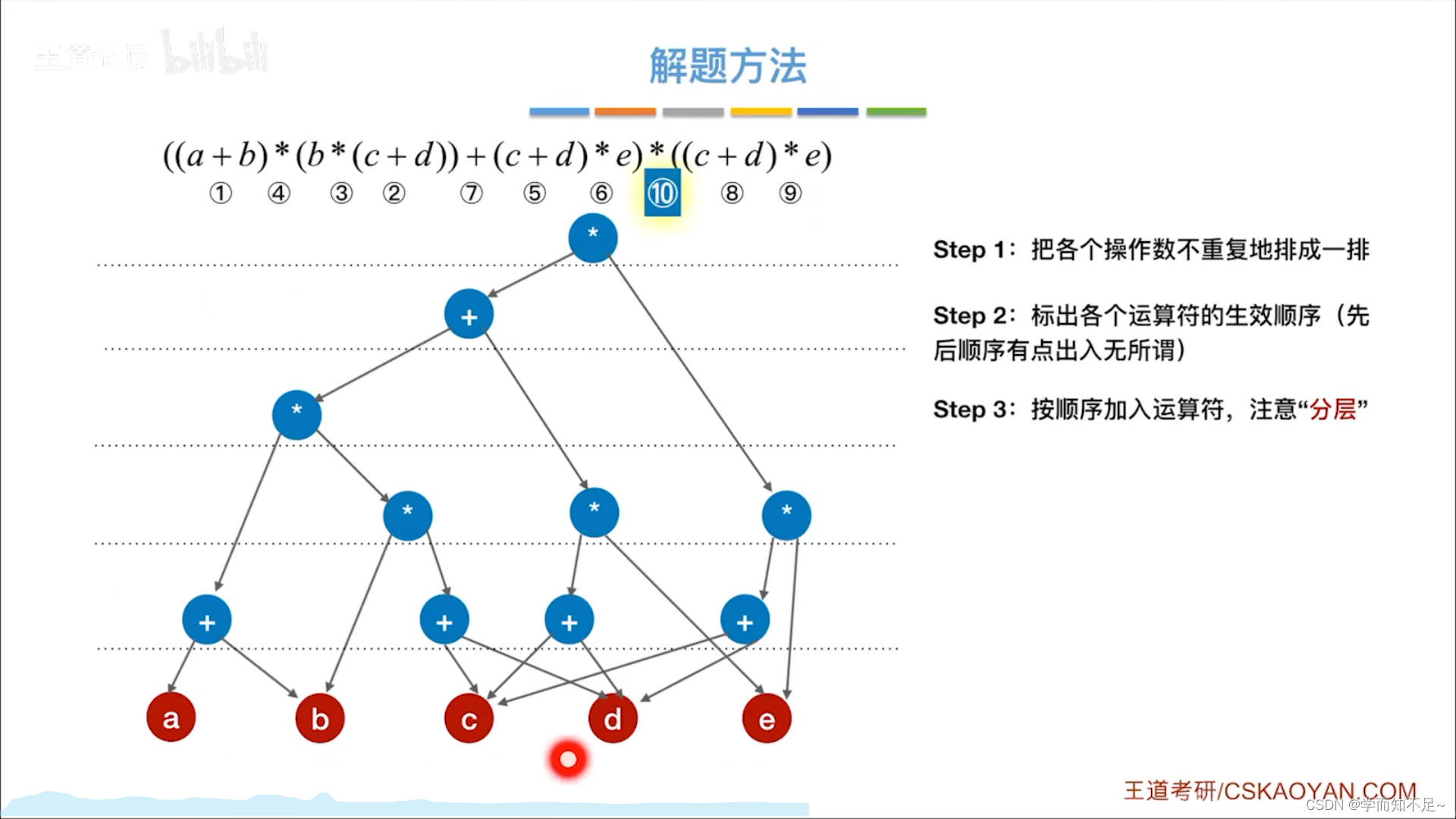
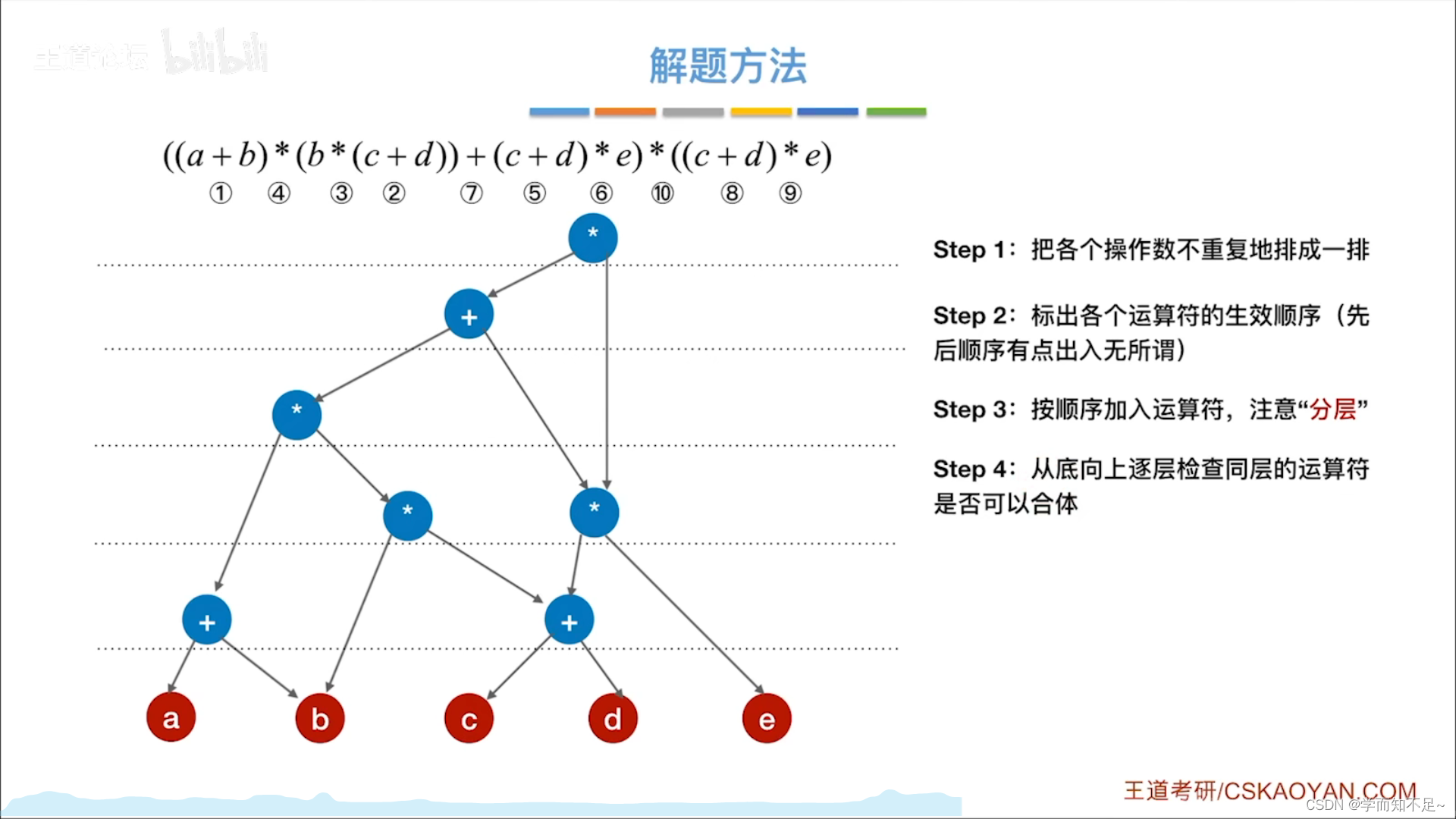
拓扑排序
AOV网
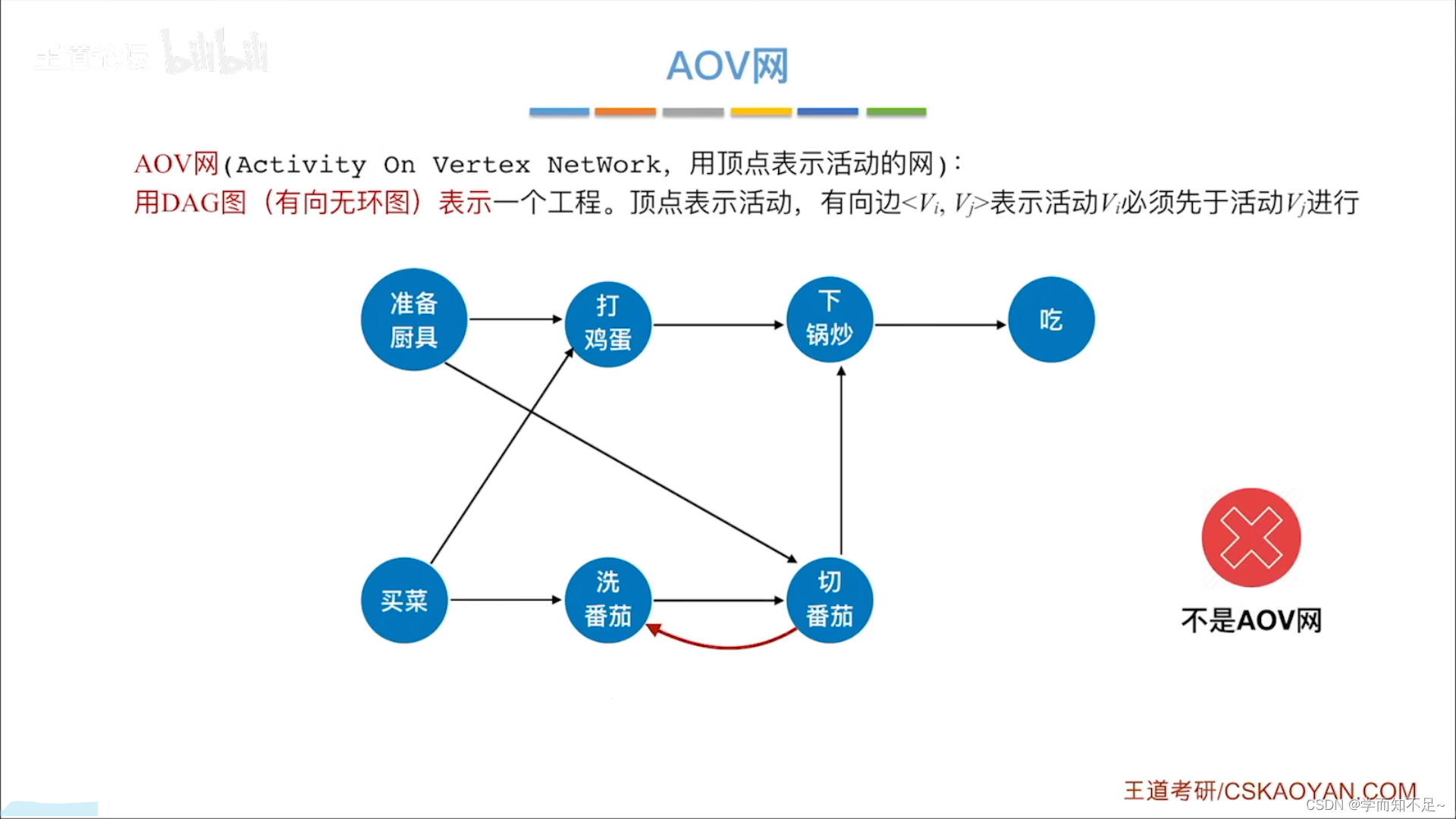
概念
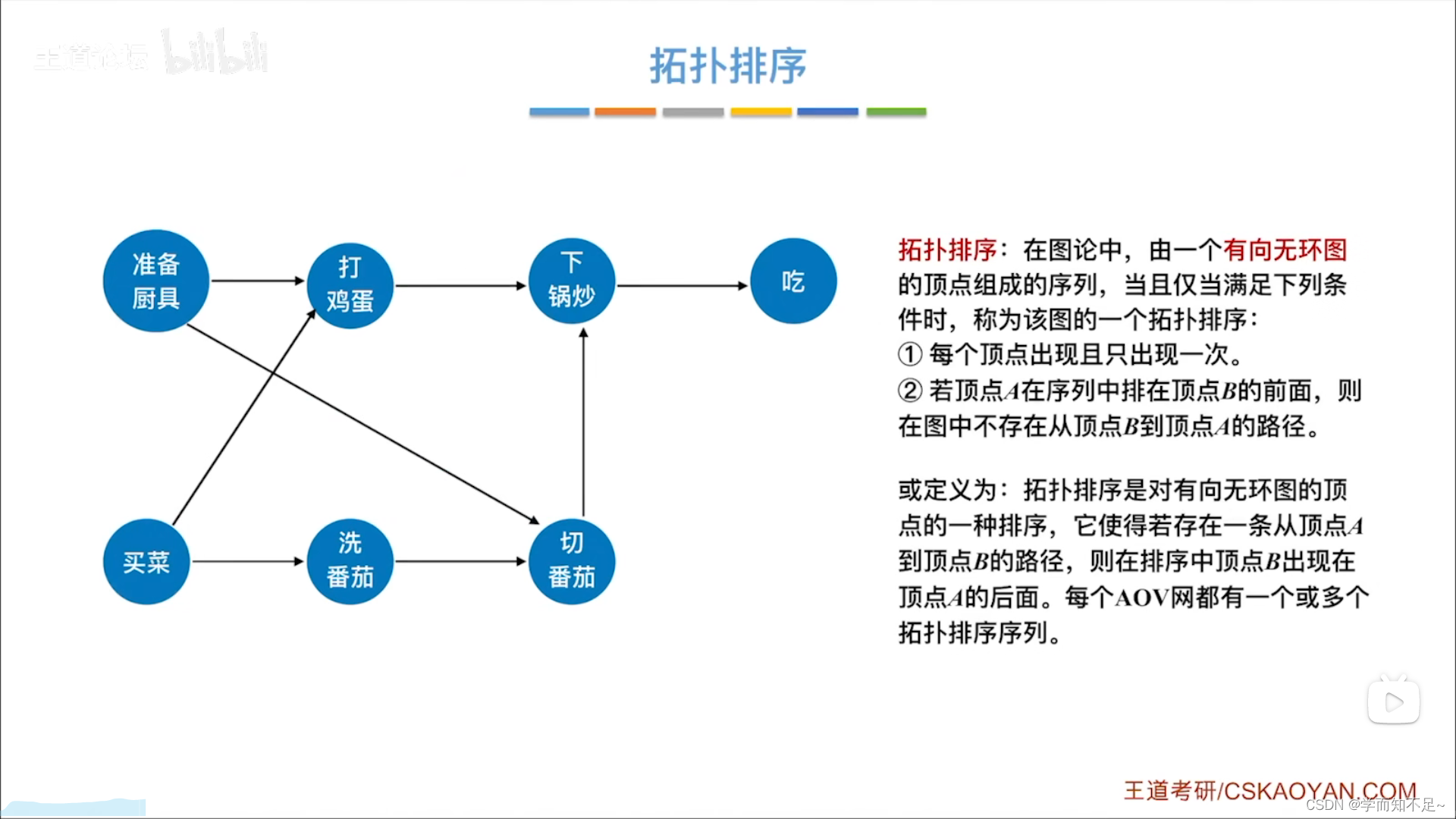

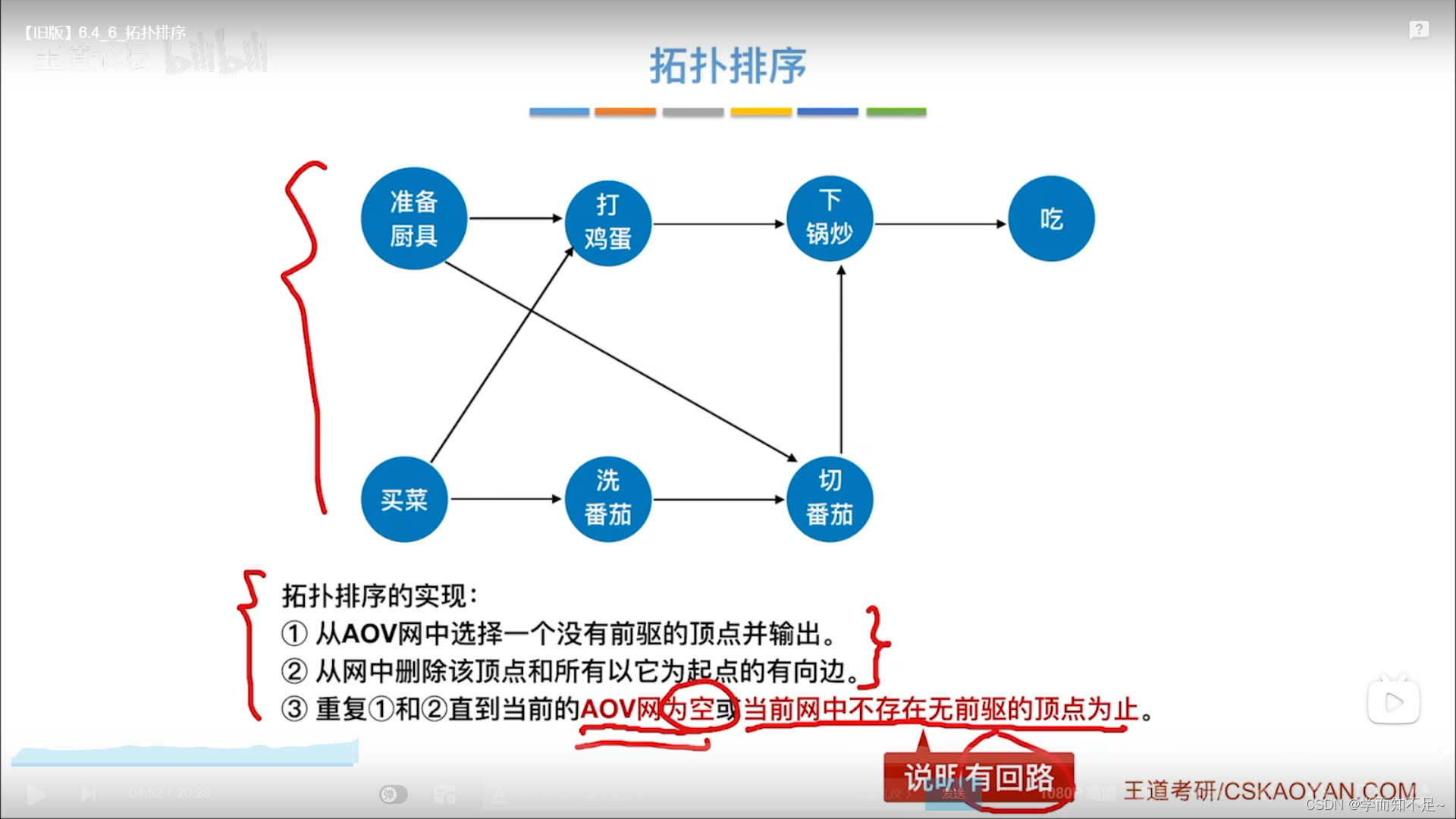
代码实现



逆拓扑排序



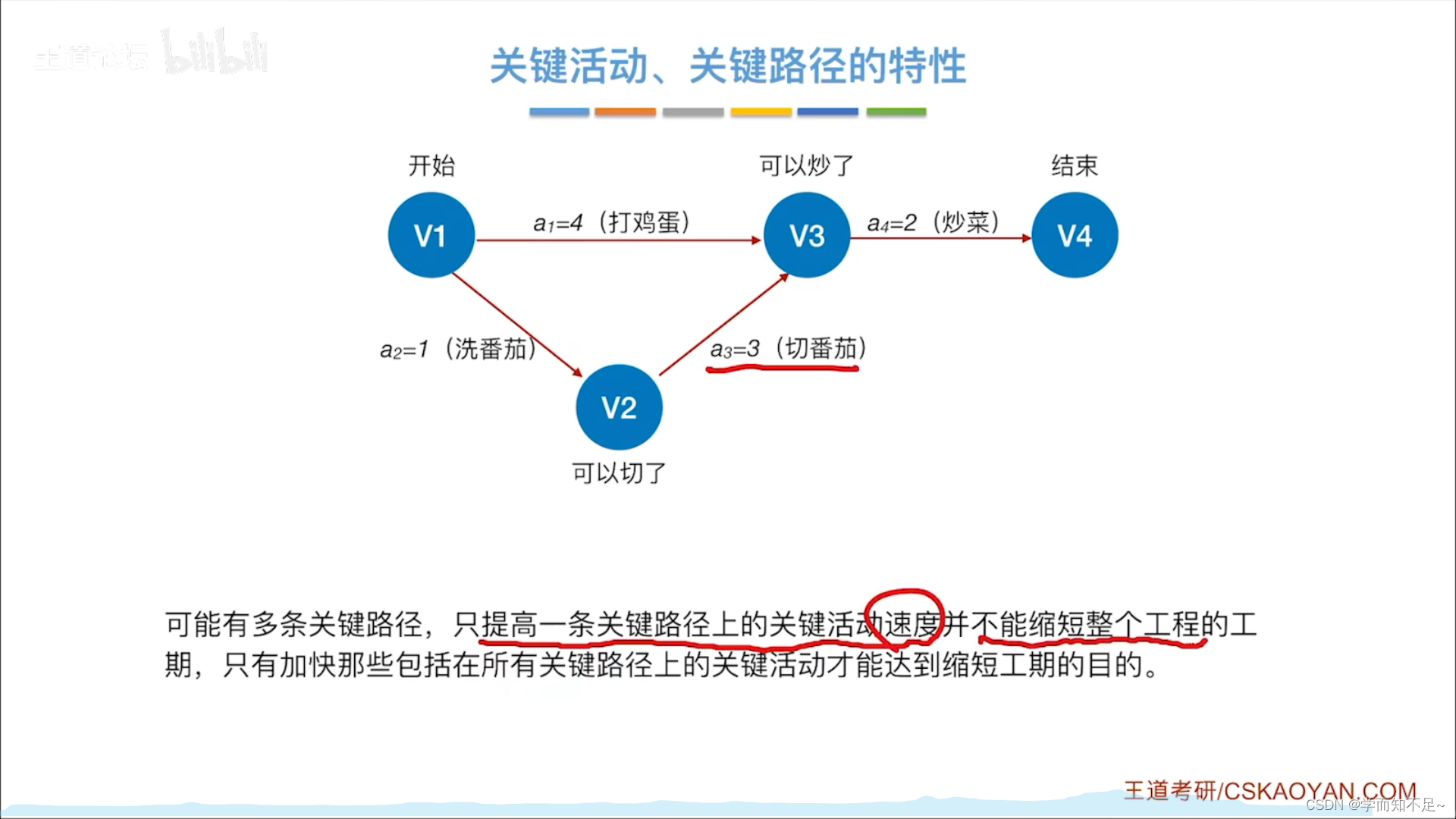
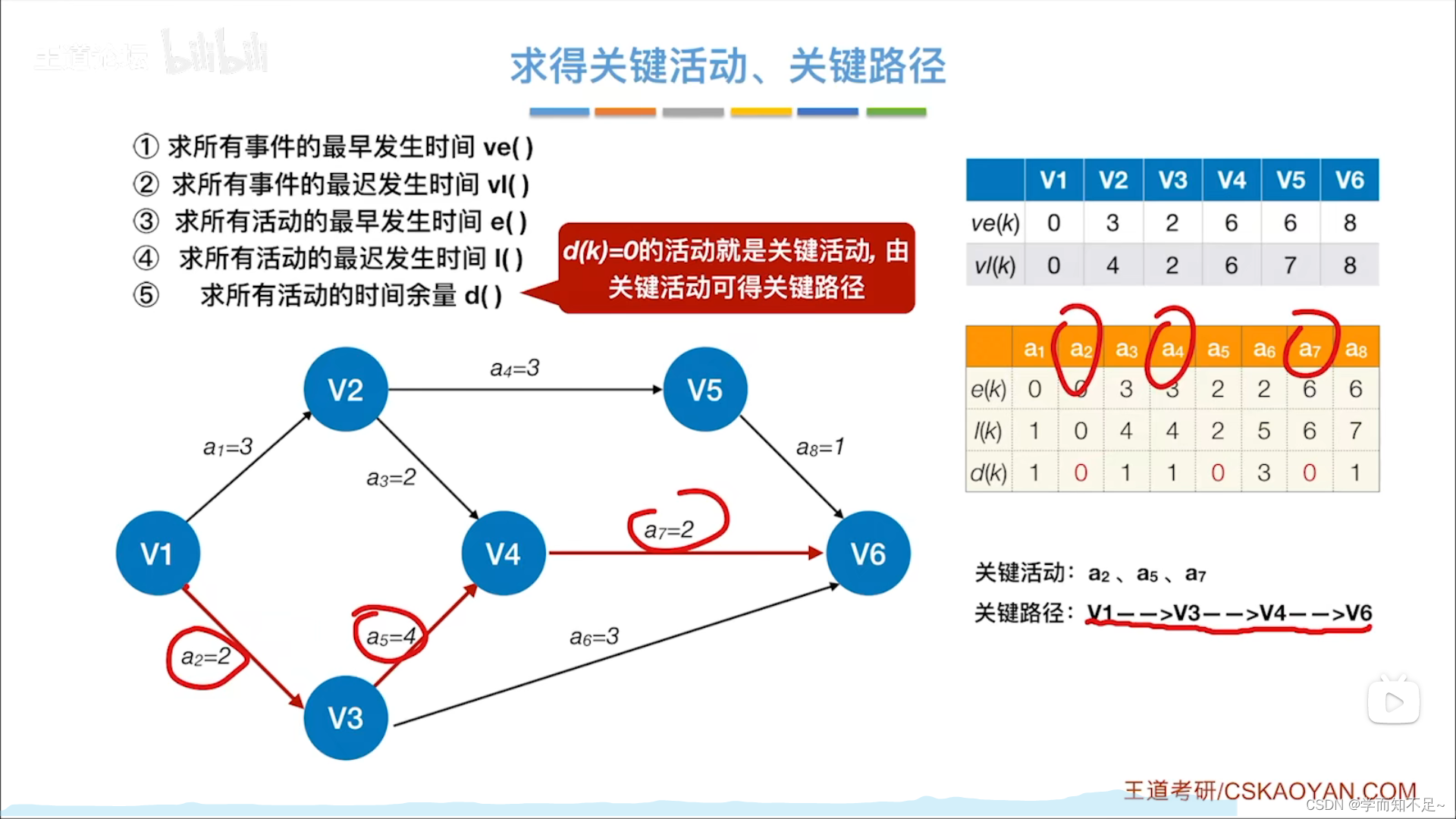
关键路径
AOE网
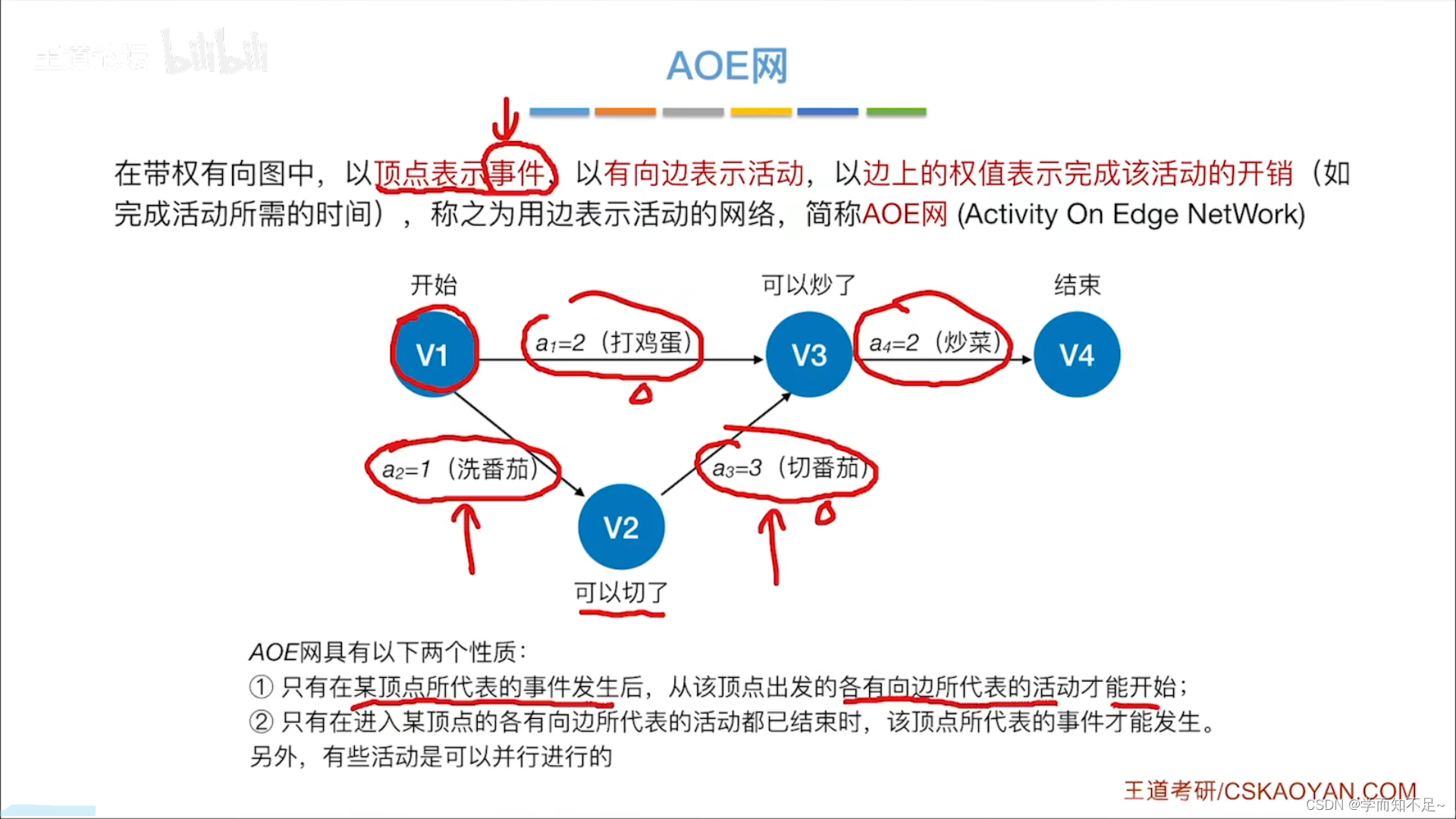
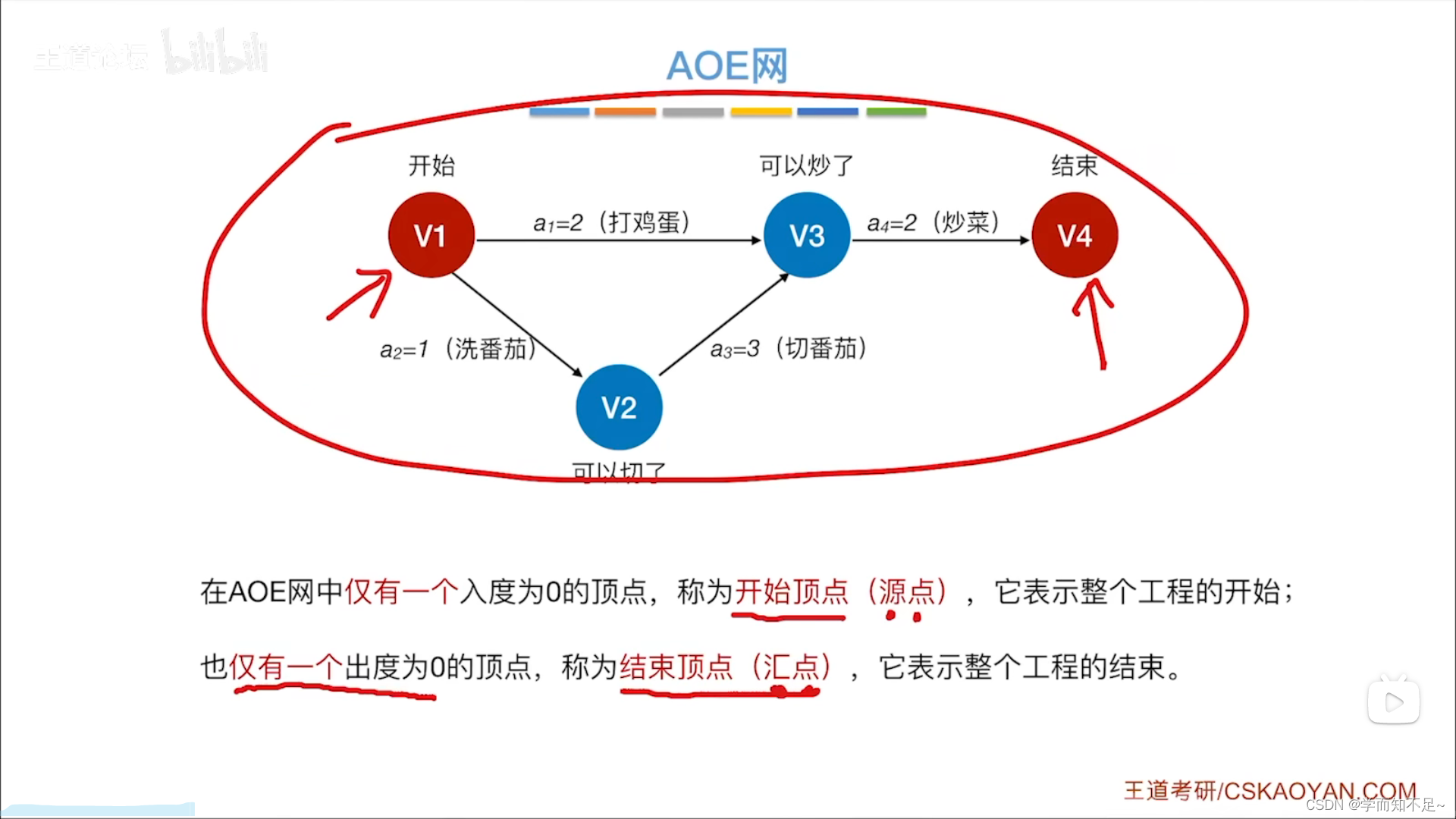
概念
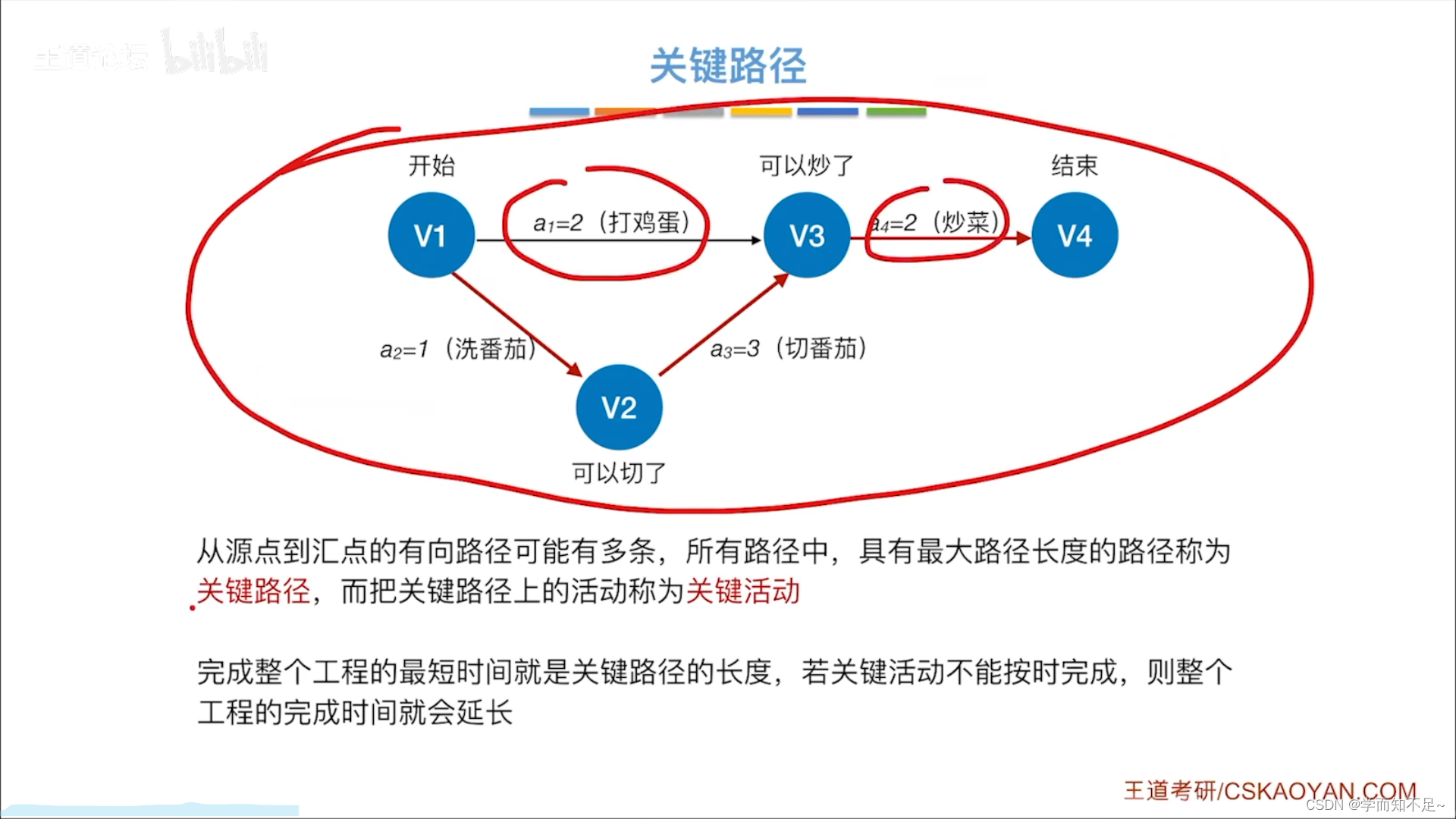

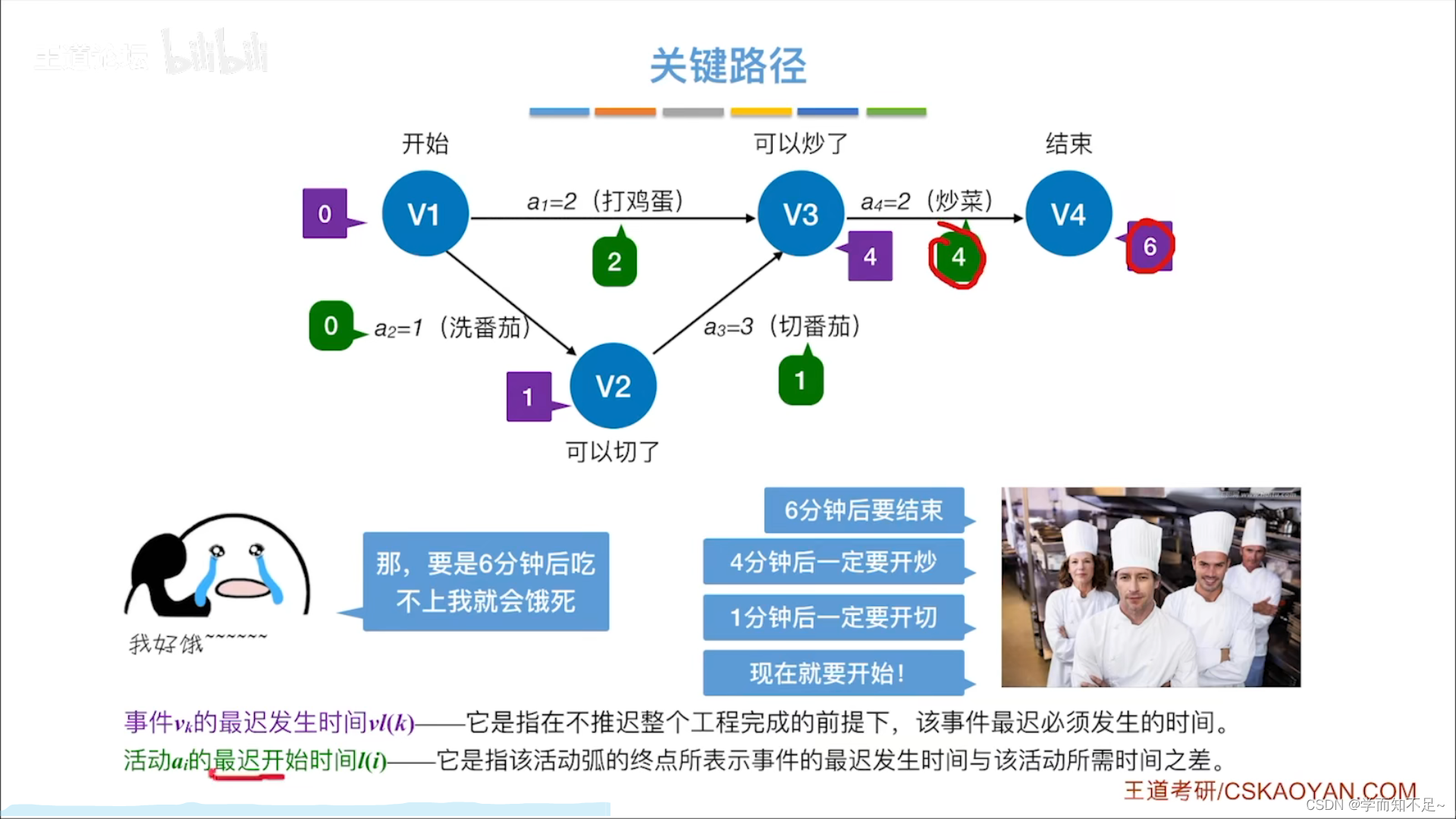

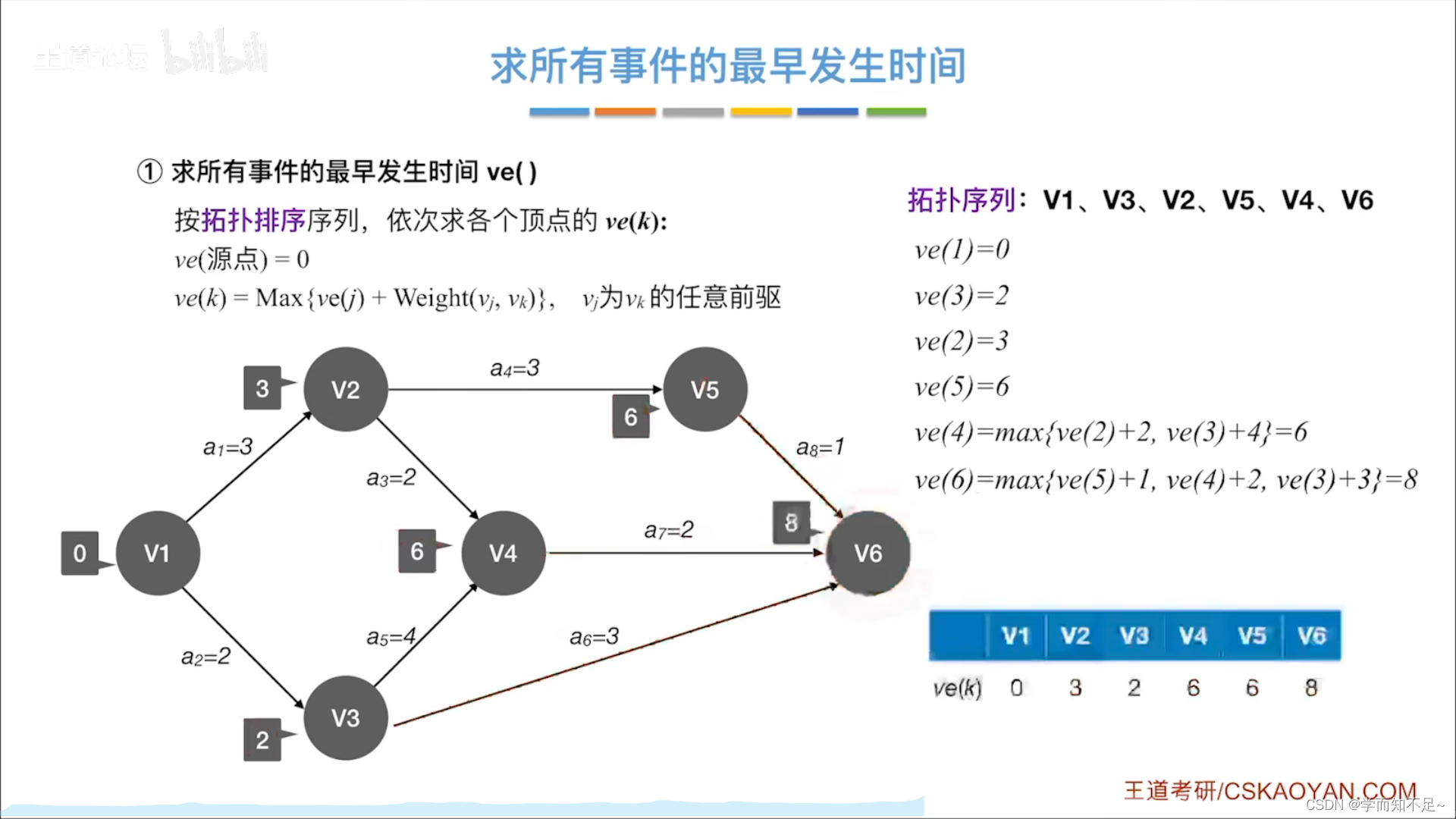
求所有事件的最早发生时间
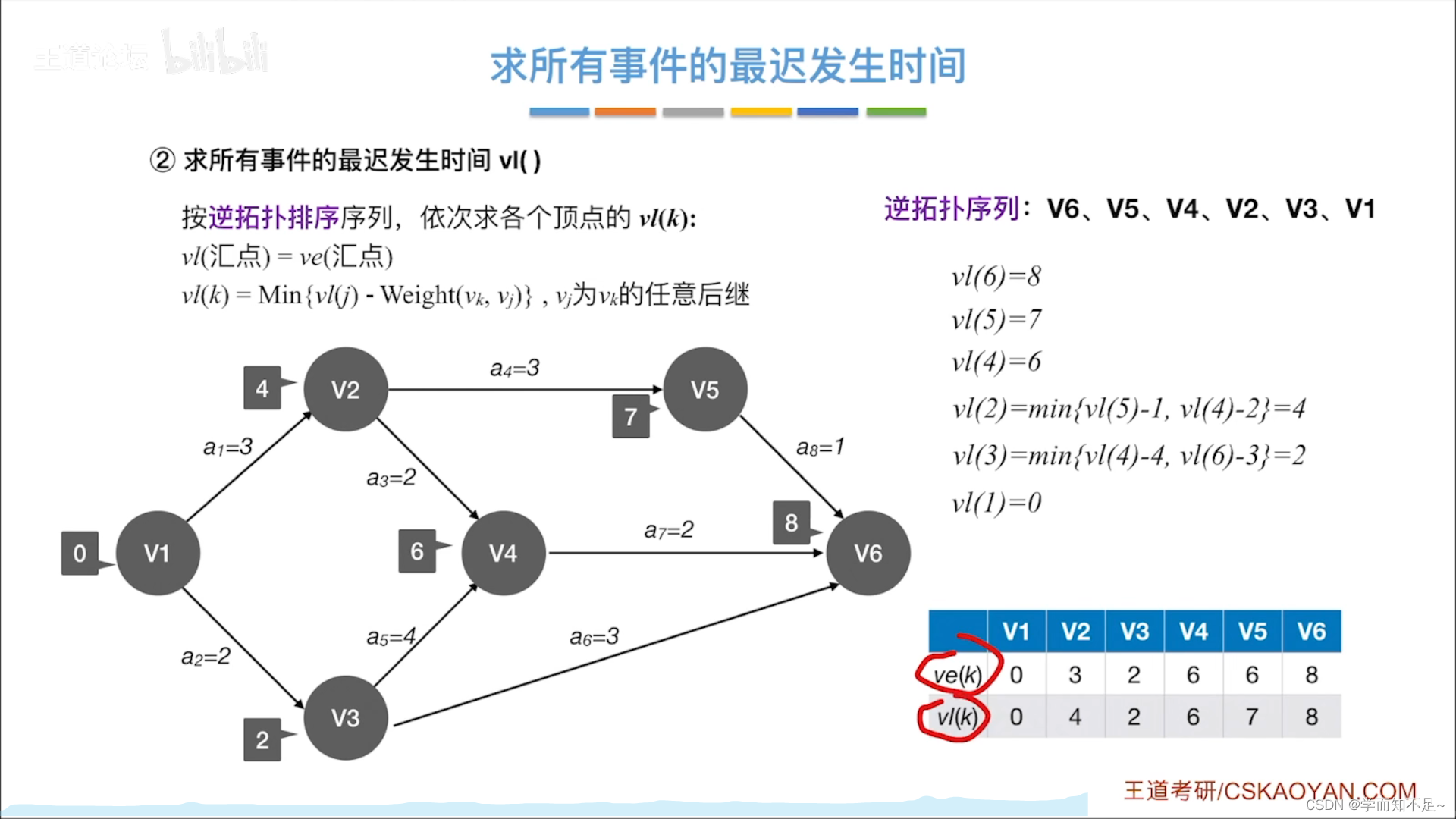
求所有事件的最迟发生时间
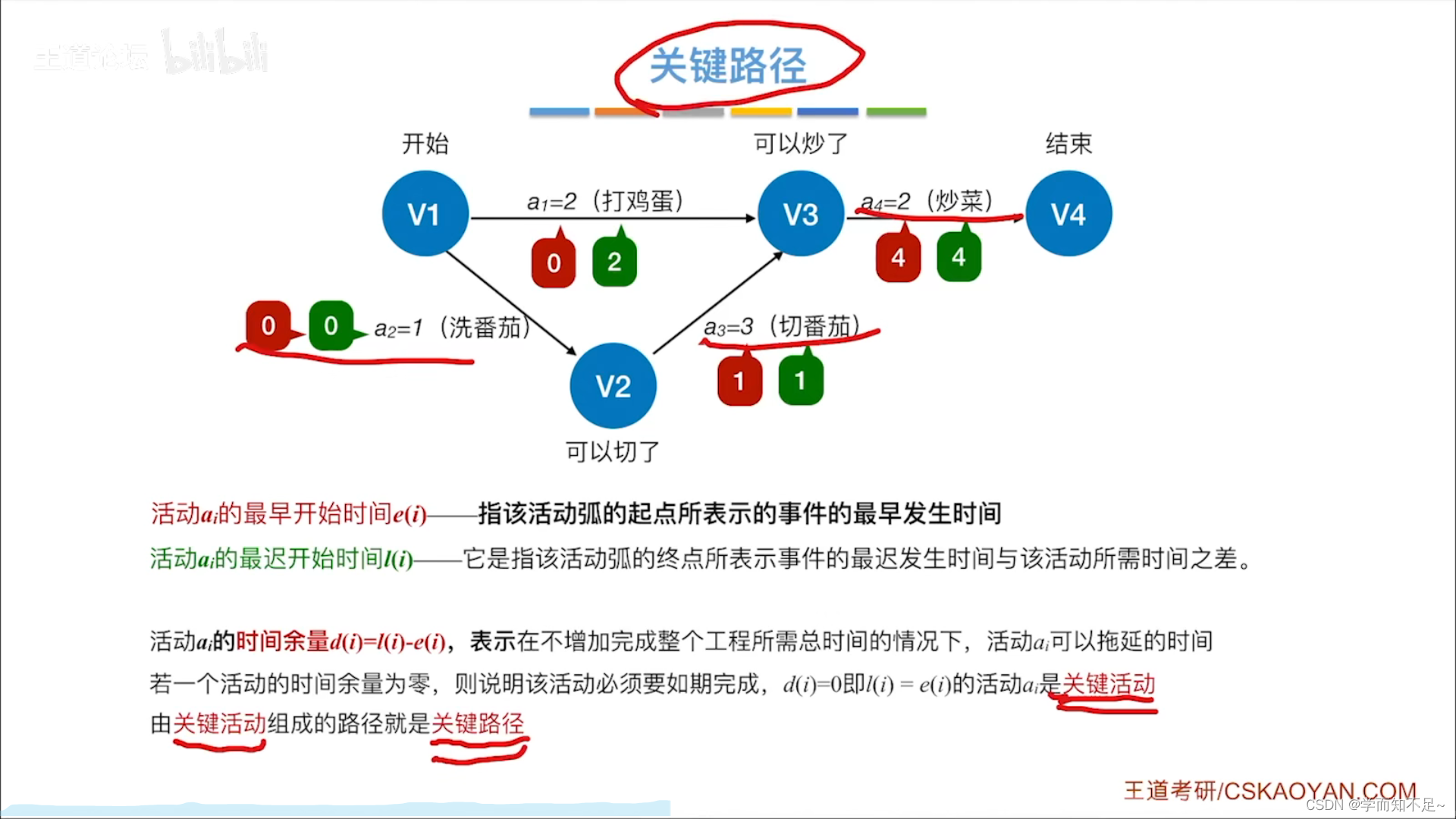
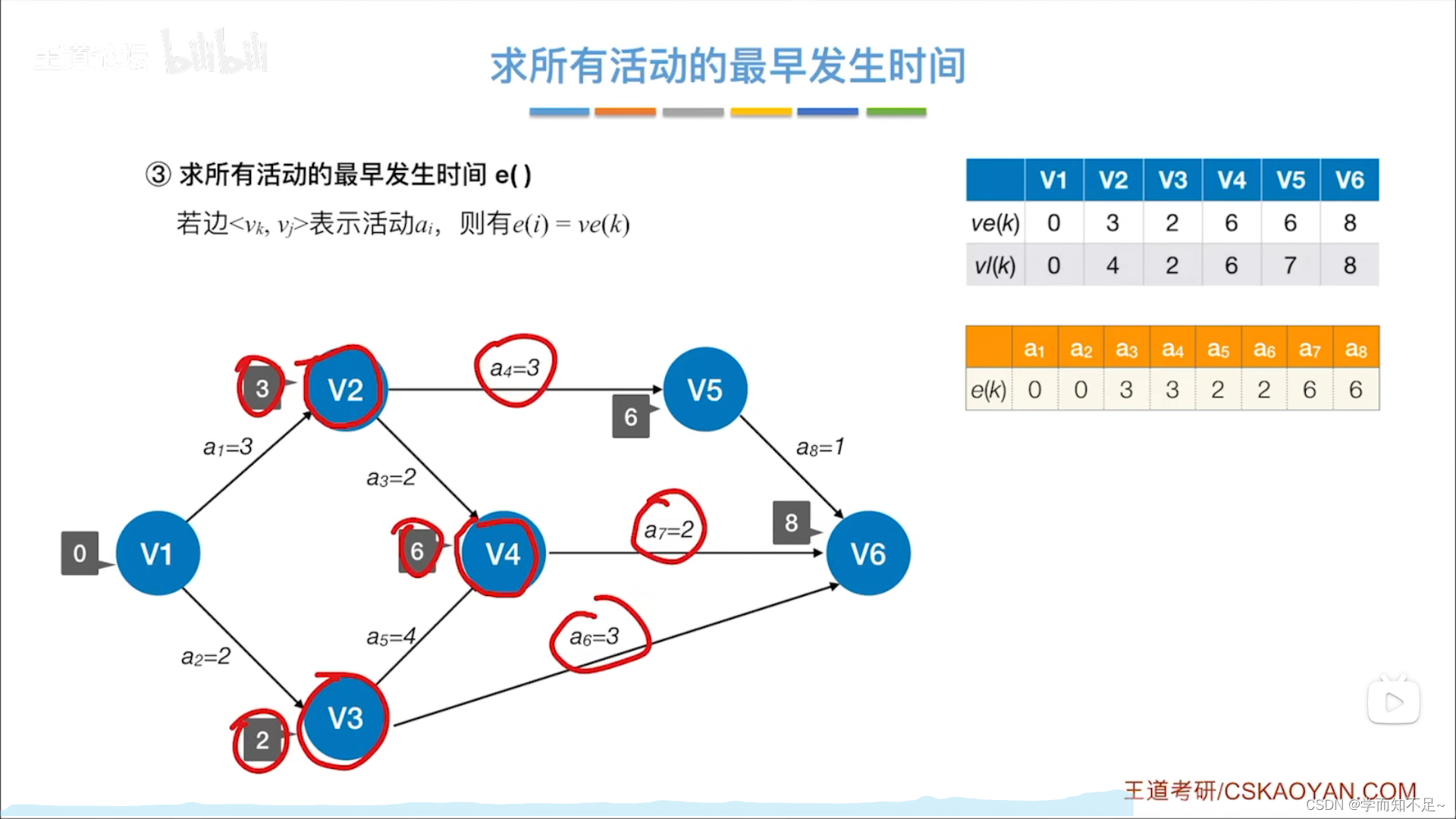
求所有活动的最早发生时间
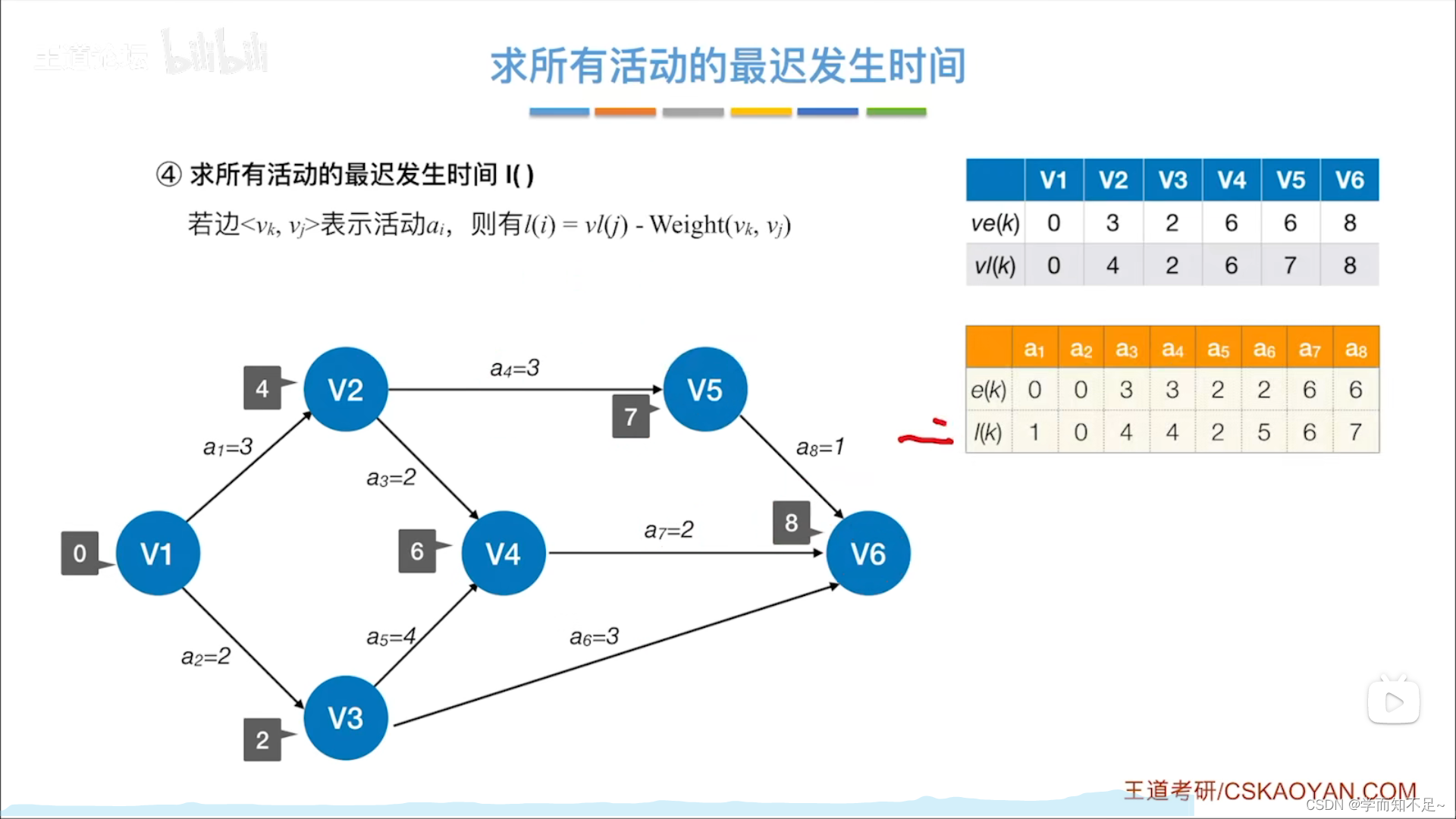
求所有活动的最迟发生时间
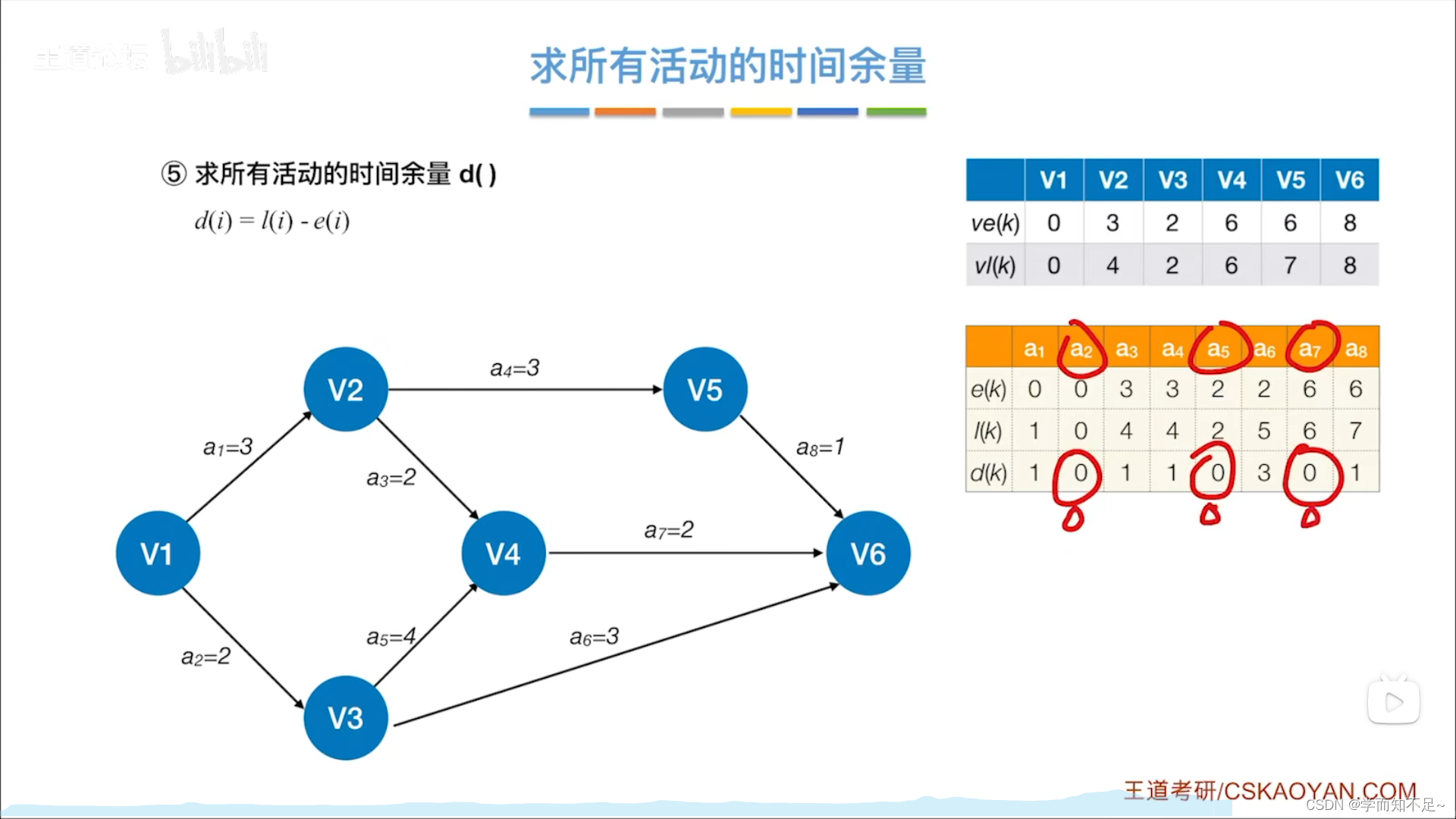
求所有活动的时间余量
求得关键活动、关键路径
关键活动、关键路径的特性