[数据结构与算法]leecode-C语言实现-6. Z 字形变换

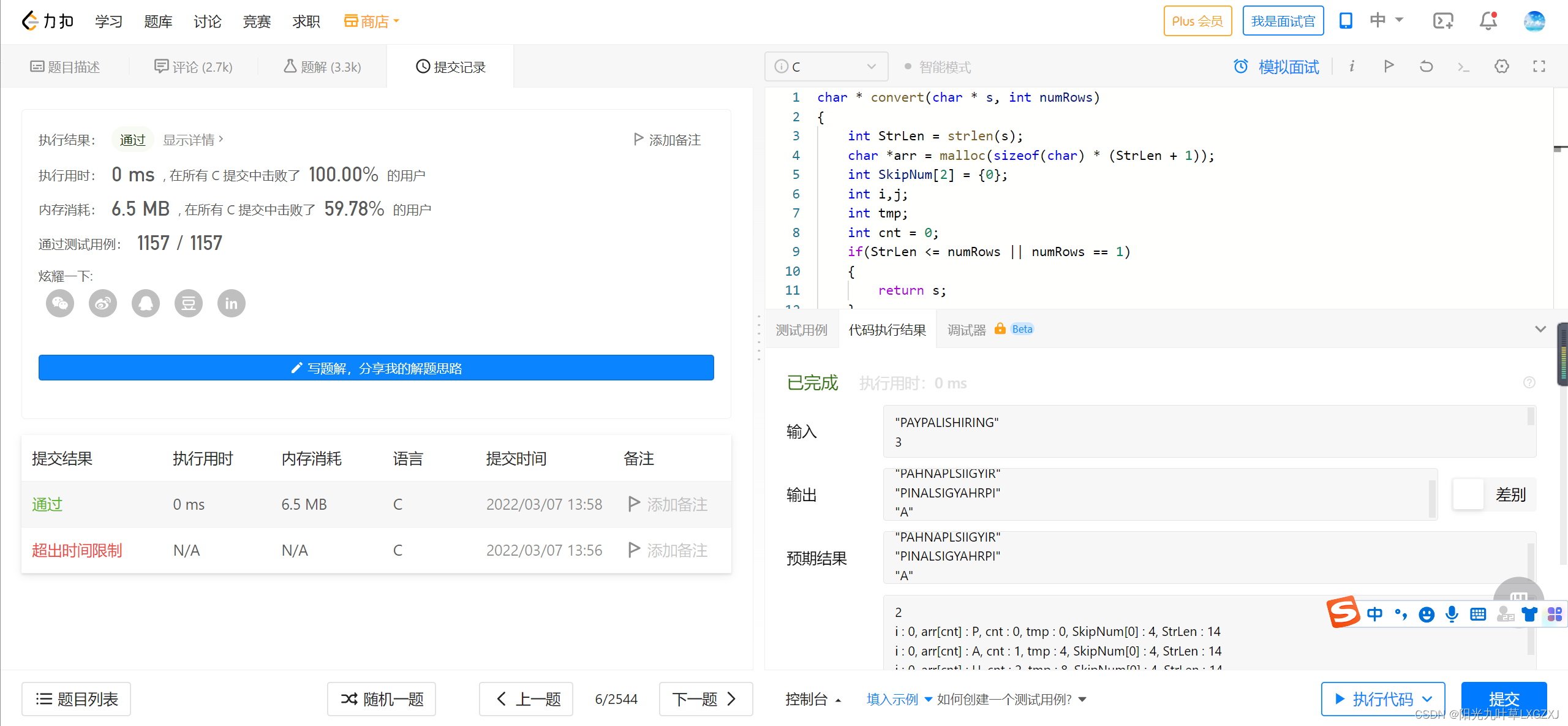
一、题目


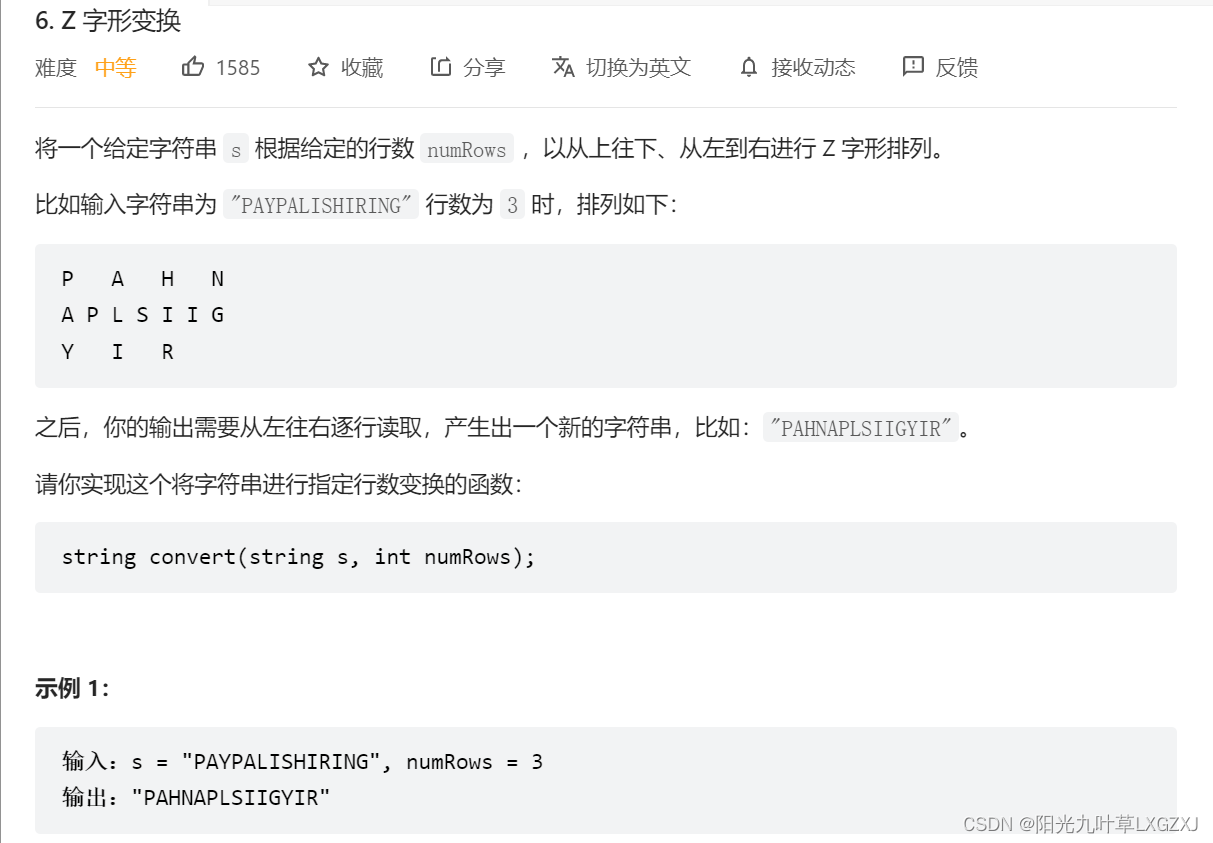
二、解题思路
列举出几种情况，来分析其中的规律，思考整体的代码逻辑和算法复杂度，再来编写代码，我的个人习惯。
举例字符串：PAYPALISHIRING
（1）行数：3
P这一行：P>A>Y>P>A，跳到第四个字符到A，再跳四个到H，再到N。
A这一行：A>Y>P，跳到第二个字符到P，P>A>L，再跳两个到L，再到S，I，I，G。
Y这一行：Y>P>A>L>I，跳到第四个字符到I，再跳四个到R。
跳4
跳2 跳2
跳4

（2）行数：4
P这一行：P>A>Y>P>A>L>I，跳到第6个字符到I，再跳六个到到N。
A这一行：A>Y>P>A>L，跳到第四个字符到L，L>I>S，再跳两个到S，再跳四，再跳二。
Y这一行：Y>P>A，跳到第两个字符到A，再跳四个到H，再跳二。
P这一行：P>A>L>I>S>H>I，跳到第6个字符到I。
跳6
跳4 跳2
跳2 跳4
跳6

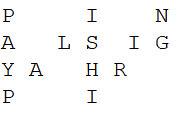
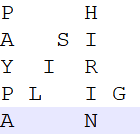
（3）行数：5
我们可以根据上面的两个例子大致推算出规律。
首尾两行每次移动固定的距离到达这一行的下一个元素，假设行数为n，首尾两行移动的距离为(n - 1) * 2，为8，我们在推算一下对不对，P>A>Y>P>A>L>I>S>H。
中间的三行，规律为每次需要跳跃两种不同的距离且循环往复，直到超过字符串最大长度，第一种：(n - 1) * 2 - 2 * 第几行（行数指0，1，2，3，4），我们算一下A开头的，(5 - 1) * 2 - 2 * 1为6。第二种：(n- 1) * 2 - 第一种，为2。
其它行数以此规律以此类推即可得到跳跃的步数。
跳8
跳6 跳2
跳4 跳4
跳2 跳6
跳8

三、虚机测试代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void main()
{
    void PrintfArr(void *arr, int size ,int elementsize);
    char * convert(char * s, int numRows);
    char s[] = "AB";
    int  numRows = 1;

    PrintfArr(s,sizeof(s) / sizeof(char),sizeof(char));

    char *res = convert(s, numRows);
    int i;

    for(i=0; res[i] != '\0'; i++)
    {
        printf("%c",res[i]);
    }
    printf("\n");
}

char * convert(char * s, int numRows)
{
    int StrLen = strlen(s);
    char *arr = malloc(sizeof(char) * (StrLen + 1));
    int SkipNum[2] = {0};
    int i,j;
    int tmp;
    int cnt = 0;
    if(StrLen <= numRows || numRows == 1)
    {
        return s;
    }
    for(i=0; i<numRows; i++)
    {
        tmp = i;
        if(i != numRows-1 && i != 0)
        {
            printf("1\n");
            SkipNum[0] = (numRows - 1) * 2 - 2 * i;
            SkipNum[1] = (numRows - 1) * 2 - SkipNum[0];
            
        }
        else
        {
            printf("2\n");
            SkipNum[0] = (numRows - 1) * 2;
            SkipNum[1] = 0;
        }
        while(tmp < StrLen)
        {
            for(j=0; j<2; j++)
            {
                if(tmp >= StrLen)
                {
                    break;
                }
                else if(SkipNum[j] != 0)
                {
                    arr[cnt] = s[tmp];
                    printf("i : %d, arr[cnt] : %c, cnt : %d, tmp : %d, SkipNum[%d] : %d, StrLen : %d\n",i,arr[cnt],cnt,tmp,j,SkipNum[j],StrLen);
                    cnt++;
                    tmp = tmp + SkipNum[j];
                }
            }
        }
    }
    arr[cnt] = '\0';
    return arr;
}

void PrintfArr(void *arr, int size ,int elementsize)
{
    if(elementsize == sizeof(int))
    {
        int *tmparr = (int*)arr;
        int i;
        for(i=0; i<size; i++)
        {
            printf("%d ",tmparr[i]);
        }
    }
    else if(elementsize == sizeof(char))
    {
        char *tmparr = (char*)arr;
        int i;
        for(i=0; i<size; i++)
        {
            printf("%c ",tmparr[i]);
        }
    }
    printf("\n========================\n");
}

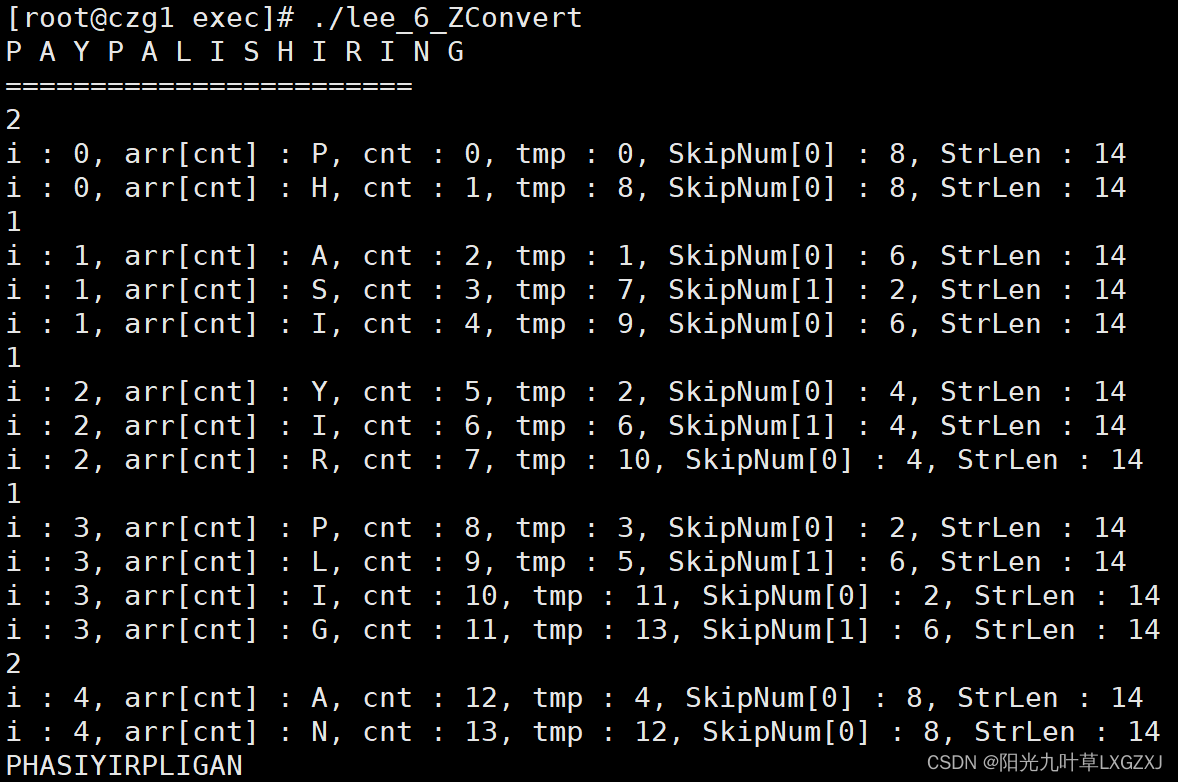
四、虚机测试截图

五、leecode提交代码

char * convert(char * s, int numRows)
{
    int StrLen = strlen(s);
    char *arr = malloc(sizeof(char) * (StrLen + 1));
    int SkipNum[2] = {0};
    int i,j;
    int tmp;
    int cnt = 0;
    if(StrLen <= numRows || numRows == 1)
    {
        return s;
    }
    for(i=0; i<numRows; i++)
    {
        tmp = i;
        if(i != numRows-1 && i != 0)
        {
            SkipNum[0] = (numRows - 1) * 2 - 2 * i;
            SkipNum[1] = (numRows - 1) * 2 - SkipNum[0];
        }
        else
        {
            SkipNum[0] = (numRows - 1) * 2;
            SkipNum[1] = 0;
        }
        while(tmp < StrLen)
        {
            for(j=0; j<2; j++)
            {
                if(tmp >= StrLen)
                {
                    break;
                }
                else if(SkipNum[j] != 0)
                {
                    arr[cnt] = s[tmp];
                    cnt++;
                    tmp = tmp + SkipNum[j];
                }
            }
        }
    }
    arr[cnt] = '\0';
    return arr;
}

六、leecode代码运行截图