二叉树
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。
1.定义
二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树。
简单理解就是:二叉树的每个子节点都只有0-2个子节点。
如下图所示的都是二叉树:

2.特点
每个节点最多只能有两棵子树,且有左右之分
如果用数组来表示二叉树,则满足:
- 子节点i的父节点的索引是: Math.floor((i - 1) / 2)
- 父节点i的左孩子节点的索引是: i * 2 + 1
- 父节点i的右孩子节点的索引是: i * 2 + 2
3. 特殊类型的二叉树
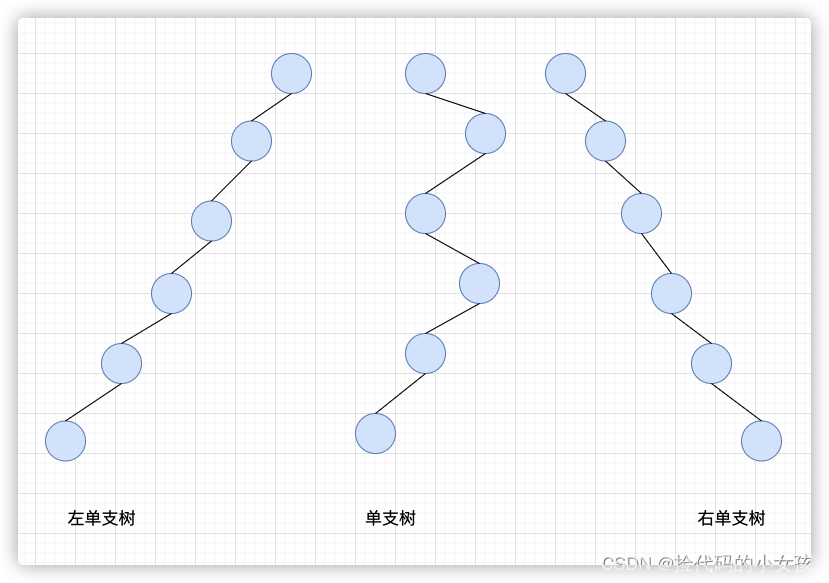
单支树
单支树就是每个树的父节点只有0-1的子节点。其中单子树又可以再划分出(左)单子树和(右)。
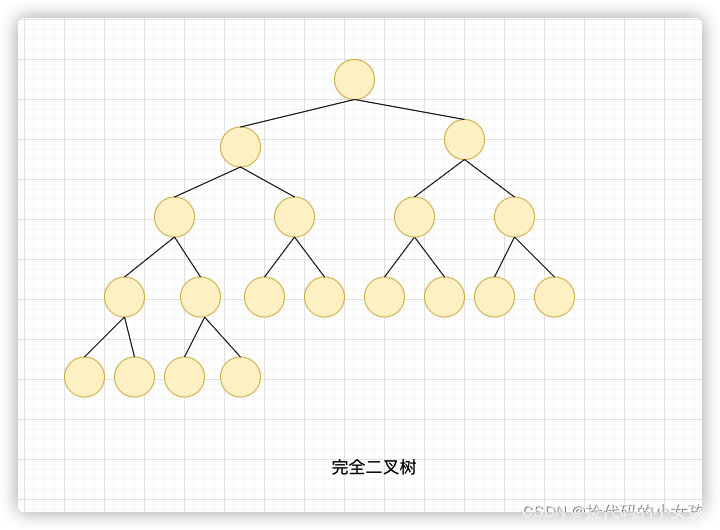
完全二叉树
深度为k,有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时,称为完全二叉树。
我的理解:深度k-1层是满的,只有第k层不满,子节点且按照从左至右排列。
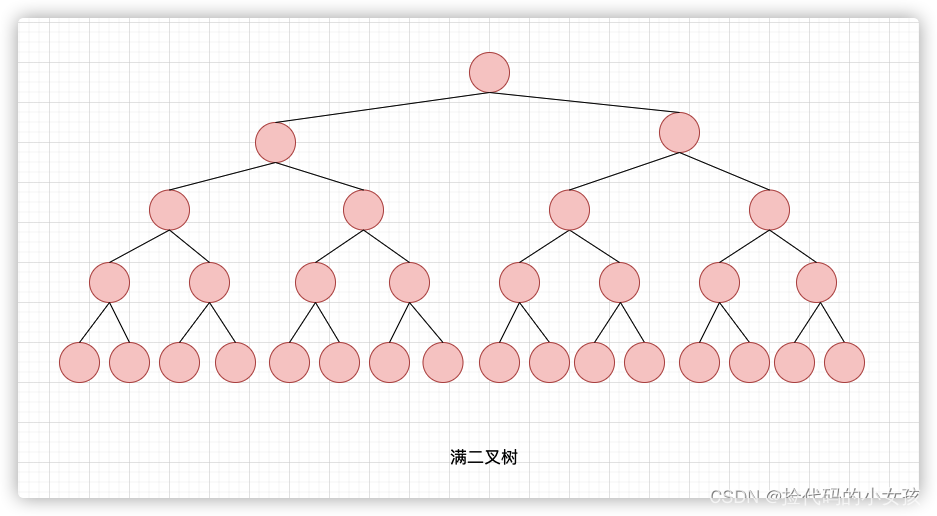
满二叉树
如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。
我的理解:最后一层的节点的子节点数都为0,其余层的子节点数都为2.