数据结构
数组和链表
数组特点
1.连续:顺序存储。
2.定长:一旦定义后,长度不可变。
3.根据下标可直接访问到这个下标的元素。
4.不适合做插入删除等操作。
python中,list列表为动态数组
链表特点
1.可以不连续。
2.不定长。
3.无法根据下标去直接访问,必须从头一个一个往后找。
4.适合做插入删除等操作。
队列和栈
队列
队列特点
1.先进先出
2.只能从队列末尾插入数据
3.只能从队列头部取出数据
class Queue(object):
def __init__(self):
self.data_list = []
def init_queue(self):
self.data_list = []
def insert(self, data):
self.data_list.append(data)
def pop(self):
if len(self.data_list) == 0:
return None
data = self.data_list[0]
del self.data_list[0]
return data
def size(self):
return len(self.data_list)
queue = Queue()
print(queue.size())
queue.insert(1)
queue.insert(2)
queue.insert(3)
head = queue.pop()
print(head)
head = queue.pop()
print(head)
head = queue.pop()
print(head)
head = queue.pop()
print(head)
栈
栈特点
1.后进先出。
2.只能从尾部插入数据。
3.只能从尾部取出数据。
class Stack(object):
def __init__(self):
self.data_stack = []
def init_Stack(self):
self.data_stack = []
def insert(self, data):
self.data_stack.append(data)
def pop(self):
if len(self.data_stack) == 0:
return None
data = self.data_stack[-1]
del self.data_stack[-1]
return data
def size(self):
return len(self.data_stack)
stack = Stack()
stack.insert(1)
stack.insert(2)
stack.insert(3)
tail = stack.pop()
print(tail)
tail = stack.pop()
print(tail)
tail = stack.pop()
print(tail)
tail = stack.pop()
print(tail)
树
多棵树组成森林。
二叉树
二叉树是每个节点最多有两个子节点的树。
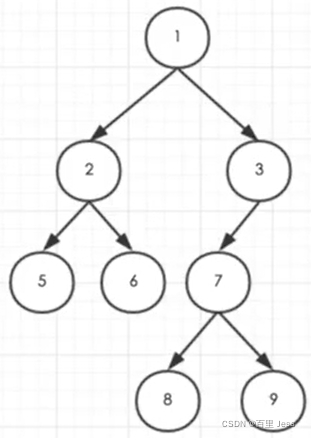
前序遍历(根左右)
前序遍历顺序:
[1, 2, 5, 6, 3, 7, 8, 9]
中序遍历(左根右)
中序遍历顺序:
[5, 2, 6, 1, 8, 7, 9, 3]
后序遍历(左右根)
后序遍历顺序:
[ 5, 6, 2, 8, 9, 7, 3, 1]
python实现二叉树
class Node(object):
def __init__(self, index):
self.index = index
self.left_child = None
self.right_child = None
class BinaryTree(object):
def __init__(self, root):
self.root = root
# 前序
def pre_travel(self, node):
if not node:
return
print(node.index)
self.pre_travel(node.left_child)
self.pre_travel(node.right_child)
# 中序
def inner_travel(self, node):
if not node:
return
self.inner_travel(node.left_child)
print(node.index)
self.inner_travel(node.right_child)
# 后序
def order_travel(self, node):
if not node:
return
self.order_travel(node.left_child)
self.order_travel(node.right_child)
print(node.index)
if __name__ == '__main__':
node_dict = {}
for i in range(1, 10):
node_dict[i] = Node(i)
node_dict[1].left_child = node_dict[2]
node_dict[1].right_child = node_dict[3]
node_dict[2].left_child = node_dict[5]
node_dict[2].right_child = node_dict[6]
node_dict[3].left_child = node_dict[7]
node_dict[7].left_child = node_dict[8]
node_dict[7].right_child = node_dict[9]
tree = BinaryTree(node_dict[1])
tree.pre_travel(node_dict[1])
tree.inner_travel(node_dict[1])
tree.order_travel(node_dict[1])
排序
排序算法
插入排序
原始数组插入到新的(sorted)数组
冒泡排序
交换
快速排序(最经典)
选一个标杆值
def quick_sort(origin_list, start, end):
if start >= end:
return
left = start
right = end
flag_index = left
while left < right:
while right > left:
if origin_list[right] < origin_list[flag_index]:
origin_list[right], origin_list[flag_index] = origin_list[flag_index], origin_list[right]
flag_index = right
break
right -= 1
while left < right:
if origin_list[left] > origin_list[flag_index]:
origin_list[left], origin_list[flag_index] = origin_list[flag_index], origin_list[left]
flag_index = left
break
left += 1
quick_sort(origin_list, start, flag_index)
quick_sort(origin_list, flag_index + 1, end)
origin_list = [5, 3, 1, 7, 9, 8]
quick_sort(origin_list, 0, len(origin_list) - 1)
print(origin_list)
归并排序
每次均分成两份,一生二,二生四,四升八,把每份排序,然后归并在一起。
二分查找
python实现二分查找
def binary_search(search_list, target):
left = 0
right = len(search_list) - 1
while left <= right:
mid = left + (right-left) // 2
if search_list[mid] < target:
left = mid + 1
continue
if search_list[mid] == target:
return mid
if search_list[mid] > target:
right = mid - 1
return None
search_list = [1, 3, 4, 6, 8, 9]
print(binary_search(search_list, 5))
print(binary_search(search_list, 1))
print(binary_search(search_list, 3))
print(binary_search(search_list, 4))
print(binary_search(search_list, 6))
print(binary_search(search_list, 8))
print(binary_search(search_list, 9))
堆
堆特点
1.堆是一个二叉树。
2.叶子节点只存在最下面两层。
3.从根节点到倒数第二层,是一个完全二叉树。
4.一个节点不可能只有右孩子。
5.一个节点的左孩子和右孩子都比这个节点大(或者小)
例如–大顶堆:

堆 python实现
class Heap(object):
def __init__(self):
self.data_list = [None]
def size(self):
return len(self.data_list) - 1
def left_child(self, root):
return root * 2
def right_child(self, root):
return root * 2 + 1
def father(self, node):
return node // 2
# 维护堆状态
def heapify(self, root):
if root > self.size():
return
left_node = self.left_child(root)
right_node = self.right_child(root)
largest = root
if left_node <= self.size():
if self.data_list[left_node] >self.data_list[largest]:
largest = left_node
if right_node <= self.size():
if self.data_list[right_node] > self.data_list[largest]:
largest = right_node
if largest != root:
self.data_list[root], self.data_list[largest] = self.data_list[largest], self.data_list[root]
self.heapify(largest)
# 建堆(最后一个非叶子节点在堆的大小除以二的地方)
def build_heap(self):
for i in range(self.size()//2, 0, -1):
self.heapify(i)
# 取堆顶
def get_max(self):
if self.size() == 0:
return None
ret = self.data_list[1]
self.data_list[1] = self.data_list[-1]
del self.data_list[-1]
self.heapify(1)
return ret
def insert(self, data):
self.data_list.append(data)
now_index = self.size()
pre = self.father(now_index)
while now_index != 1 and self.data_list[pre] < data:
self.data_list[pre], self.data_list[now_index] = self.data_list[now_index], self.data_list[pre]
now_index = pre
pre = self.father(now_index)
if __name__ == '__main__':
heap = Heap()
heap.insert(9)
heap.insert(10)
heap.insert(7)
heap.insert(12)
heap.insert(3)
heap.insert(4)
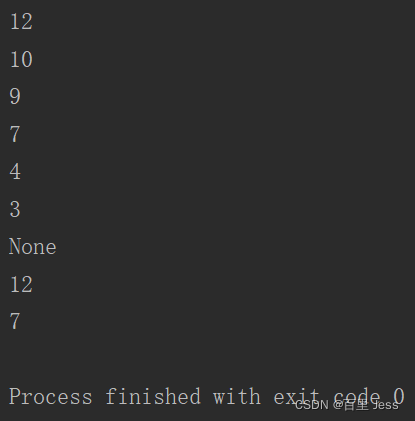
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
print(heap.get_max())
heap.insert(10)
heap.insert(9)
heap.insert(8)
heap.insert(7)
heap.insert(7)
heap.insert(12)
print(heap.get_max())
heap.data_list = [None, 1, 2, 3, 4, 5, 6, 7]
heap.build_heap()
print(heap.get_max())
运行结果