题目描述
给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 ?1。
输入格式
第一行包含整数 N,表示数列长度。
第二行包含 N 个整数,表示整数数列。
输出格式
共一行,包含 N 个整数,其中第 i 个数表示第 i 个数的左边第一个比它小的数,如果不存在则输出 ?1。
数据范围
1≤N≤105
1≤数列中元素≤109
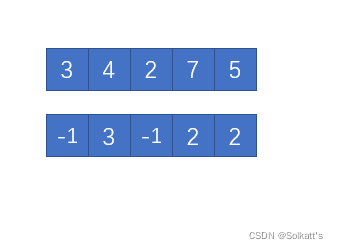
输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
思路
这是一道经典的单调栈的运用,本题只需要一直维持一个单调栈即可。
我们会发现,元素入栈过程中,当a[x] >= a[y]且x < y时,我们将前面大于a[y]的元素弹出维持一个新的单调栈,因为输出每个数左边第一个比它小的数不需要前面的单调子序列。举例:当2输入时,把3,4弹出(因为2前面肯定时大于的2的)当7输入,找到2即可。
代码示例
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int s[N], tt;
int main()
{
int n;
cin >> n;
while(n --)
{
int x;
cin >> x;
while(tt && s[tt] >= x) tt --;
if(tt)
{
cout << s[tt] << ' ';
}
else
{
cout << "-1" << ' ';
}
s[++ tt] = x;
}
return 0;
}
暴力码,但会超时
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int s[N], n, ans[N];
int main()
{
cin >> n;
for(int i = 0; i < n; i ++) cin >> s[i];
cout << "-1 ";
for(int i = 1; i < n; i ++)
{
int j = i - 1;
while(j >= 0)
{
if(s[j] < s[i])
{
cout << s[j] << ' ';
break;
}
j --;
}
if(j == -1) cout << "-1 ";
}
}