1. 题目描述
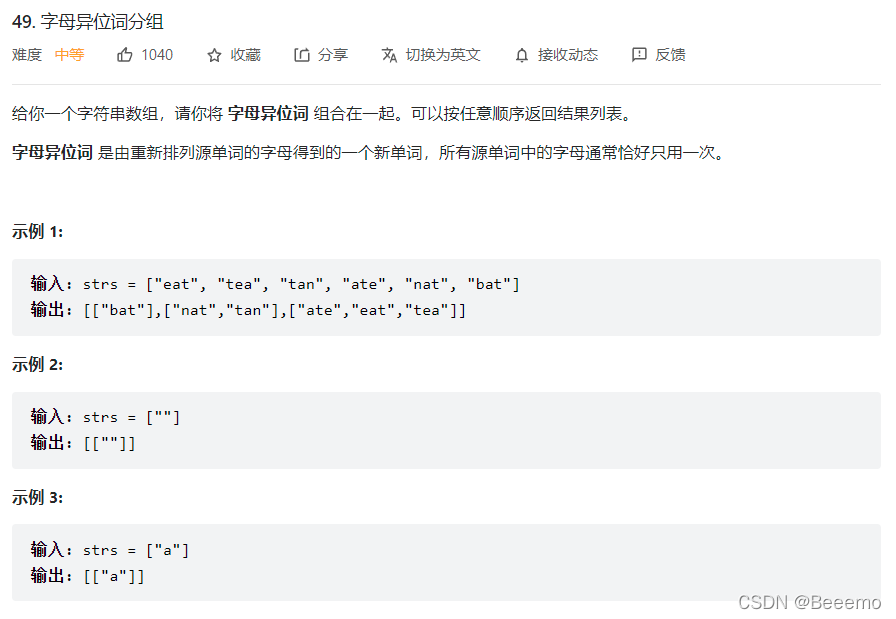
2. 解题思路
这道题目的重点在于如何判断字母异位词,这时候我首先就想起了之前做过的一道题目【LeetCode - Java】46. 全排列(中等),在全排列中所有的组合都是相互的字母异位词,那么这样说我是不是可以把字符串数组中的值读取出来,生成他们所有的全排列,判断其是否在数组中从而得出答案呢?按道理来说这样做是肯定没有问题的,但求全排列是一个时间复杂度非常高的算法,并且这里字符串的长度可达 1 0 4 10^4 104,因此这种方法显然是不合适的。
字母异位词还有什么特征?各字母出现的次数一样!那么我们可以利用哈希表对每个字符串中出现的字符进行计数统计,把该频次表作为另一个哈希表的key,在value中存放同为字母异位词的字符串 。为什么可以这样做呢?这是哈希表的特性,相同内容的哈希表他们的内存地址也是相同的, 而对于数组来说就没有这个特性,自然而然这里也就不能使用数组代替哈希表进行字母频次统计了。
那…如果我非要用数组来进行频次统计呢?如何把相同内容的不同地址数组视为相等呢?这可以从【LeetCode - Java】38. 外观数列(中等)这道题目中找到灵感。频次表的核心内容是什么?总体来说他表达的就是多少个什么字母,那么我们可以构建一个类外观数列,按照α个β字母的形式生成字符串,为防止误判可以在不同字母计数中加分隔符。
进一步简化,我可以不计数吗?如果不计数不算频次表,怎么才能够判断这个字符串中的字符个数是否一样呢?利用排序就可以实现这一想法,只需要把所有字符串都预先进行排序,那么互为字母异位词的字符串排序后的结果必定是一致的。
3. 代码实现
3.1 哈希表计数统计
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<Map<Character, Integer>, List<String>> mapListHashMap = new HashMap<>();
for (String str : strs) {
char[] chars = str.toCharArray();
HashMap<Character, Integer> map = new HashMap<>();
for (char aChar : chars) {
map.put(aChar, map.getOrDefault(aChar, 0) + 1);
}
List<String> orDefault = mapListHashMap.getOrDefault(map, new ArrayList<>());
orDefault.add(str);
mapListHashMap.put(map,orDefault);
}
return new ArrayList<>(mapListHashMap.values());
}
3.2 哈希表外观数列统计
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<String, List<String>> map = new HashMap<>();
for (String str : strs) {
char[] chars = str.toCharArray();
int[] count = new int[26];
for (char aChar : chars) {
count[aChar - 'a']++;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < count.length; i++) {
if (count[i] != 0)
sb.append(count[i]).append(i).append('.');
}
String s = sb.toString();
List<String> orDefault = map.getOrDefault(s, new ArrayList<>());
orDefault.add(str);
map.put(s, orDefault);
}
return new ArrayList<>(map.values());
}
3.3 哈希表排序统计
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<String, List<String>> map = new HashMap<>();
for (String str : strs) {
char[] chars = str.toCharArray();
Arrays.sort(chars);
String s = new String(chars);
List<String> ans = map.getOrDefault(s, new ArrayList<String>());
ans.add(str);
map.put(s, ans);
}
return new ArrayList<>(map.values());
}
3.4 对比
计数统计的时间复杂度是O(m*n),m为字符串数组的长度,n为字符串的最大长度;外观数列的时间复杂度是O(m*(n+k)),k为常数,值为26,代表英文字母的数量;排序的时间复杂度是O(mn*logn),其中进行排序的时间复杂度为O(nlogn)。
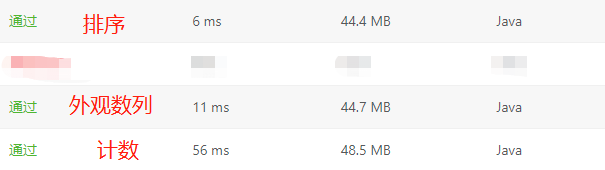
看到这里是不是觉得很疑惑呢?明明这时间复杂度都是呈递增状态的,为什么实际的测试表现却是越来越优呢?首先来解释计数与外观数列之间的差距,我曾经说到过,在一定情况下使用数组代替哈希表统计是可以大大提高速度的,其实这里本质上也是这个原因,至于那个k其实很小也可以忽略其对速度的影响,因此外观数列比计数快是合理现象。
那么排序为什么比外观数列快呢?要符合这一现象时间复杂度之间的关系必须要满足n+k>n*logn,即n+26>n*logn,为此我专门画了两个函数图对比了一下:
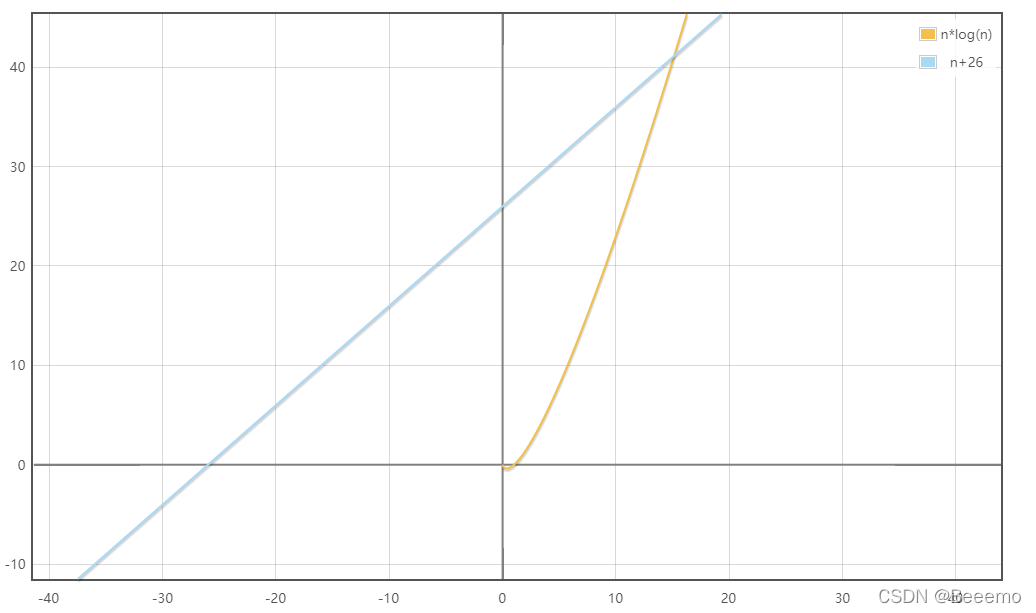
显然,当n约处于0-15的位置上时,确实会出现这种状况的,这就表明本道题目的测试用例应该很大一部分是处于这个区间范围内的,因此出现该现象也就合理了。
纠结完时间复杂度再来看看空间复杂度。计数和外观数列的空间复杂度都是O(m*(n+k)),排序的空间复杂度是O(mn),在现象上也表现合理。