文章目录
1 二分查找的基本原理
二分查找的使用情况:对于已经有序的数据来说,二分查找可以极大的提高查找效率,我们知道查找的本质就是排除,为什么二分查找可以右极高的查找效率呢?本质就是一次查找就可以排除一半无效的数据,这就是它高效的原因之一;
从时间复杂度度的角度来说:二分查找的查找效率达到 O(log n),这比遍历一遍数据的查找方式的时间复杂度O(n)好很多;特别是体现在数据量极大的情况下;
二分查找的原理也就是:要查找某一个数x,前提查找的数据是有序的,那么就可以找到该有序数据的中间位置middle,用x和middle比较,如果x比middle大,那么说明,x在middle的右边,那么就排除middle左边的所有数据(包括middle本身);如果x比middle小,那么说明,x在middle的左边,那么就可以排除middle右边的所有数据(包括middle本身);如果x == middle等于那么就说明找到了x;
2 二分查找算法的两种写法
大家对二分擦或者算法总有一种一看就会一写就废的感觉;
主要是对查找的边界控制得不够清晰;
对于边界的控制有左闭右闭的写法,也有左闭右开的写法;
两种写法都是有些微的差别,但是原理是一样的;
2.1 左闭右闭的二分查找写法
void binary_search(vector<int> nums,int x)
{
// 定义左闭右闭的区间里,[left, right]
int left = 0;
int right = nums.size() - 1;
// 当left==right,区间[left, right]依然有效,所以用 <=
while (left <= right) {
int middle = left + ((right - left) >>1);
if (nums[middle] > x) {
// x 在左区间,所以[left, middle - 1]
right = middle - 1;
} else if (nums[middle] < target) {
// target 在右区间,所以[middle + 1, right]
left = middle + 1;
} else { // nums[middle] == target
// 数组中找到目标值
}
}
//退出循环表示:left>right此时
// 未找到目标值
}
}
我们重点关注循环的边界条件:while(left<=right),为什么要用<=,而不用<,其实就是因为我们用的是左闭右闭区间的写法,此时让left==right 时候,还在区间范围内,所以要继续查找;
2.2 左闭右开的区间的写法
void binary_search(vector<int> nums,int x)
{
// 定义左闭右闭的区间里,[left, right)
int left = 0;
int right = nums.size(); //注意这里的right是比数组最后一个值的下标还多1的下标
// 当left==right,区间[left, right)无效,所以用 <
while (left < right) {
int middle = left + ((right - left) >>1);
if (nums[middle] > x) {
// x 在左区间,所以[left, middle)
//注意这里和闭区间的写法不一样
right = middle;
} else if (nums[middle] < target) {
// target 在右区间,所以[middle + 1, right)
left = middle + 1;
} else { // nums[middle] == target
// 数组中找到目标值
}
}
//退出循环表示:left>right此时
// 未找到目标值
}
}
而我们的左闭右开区间的写法:相比于左闭右闭区间的写法,在while的判断条件有所不同,还有当 x < 中间值时候,right = middle,而不是right = middle-1;因为开区间,说明middle本身就不是在数据方位内的值了,所以不用-1;
3 四道经典力扣的二分算法的题目
3.1 有效的完全平方数
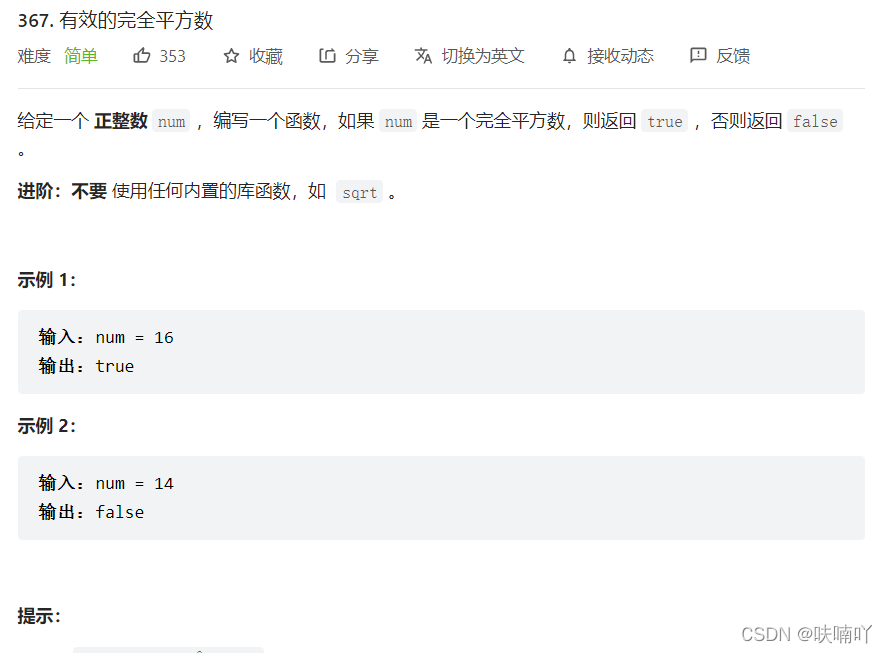
思路:只要我们在[1,num]的范围内,试数,找到一个数x ,只要满足x*x = num,那么就可以了;
此时,由于【1,num】的数都是升序,即有序,我们可以使用二分查找算法,这样查找效率更高;
代码:
class Solution {
public:
//只要在[1,num]的区间不断试数就可以
bool isPerfectSquare(int num) {
int left = 1;
int right =num;
while(left <=right)
{
long long middle = left +((right - left)>>1);
long long val = middle*middle;
if(val == num)
return true;
else if(val < num)
left = middle+1;
else
right = middle -1;
}
return false;
}
};
3.2 x 的平方根
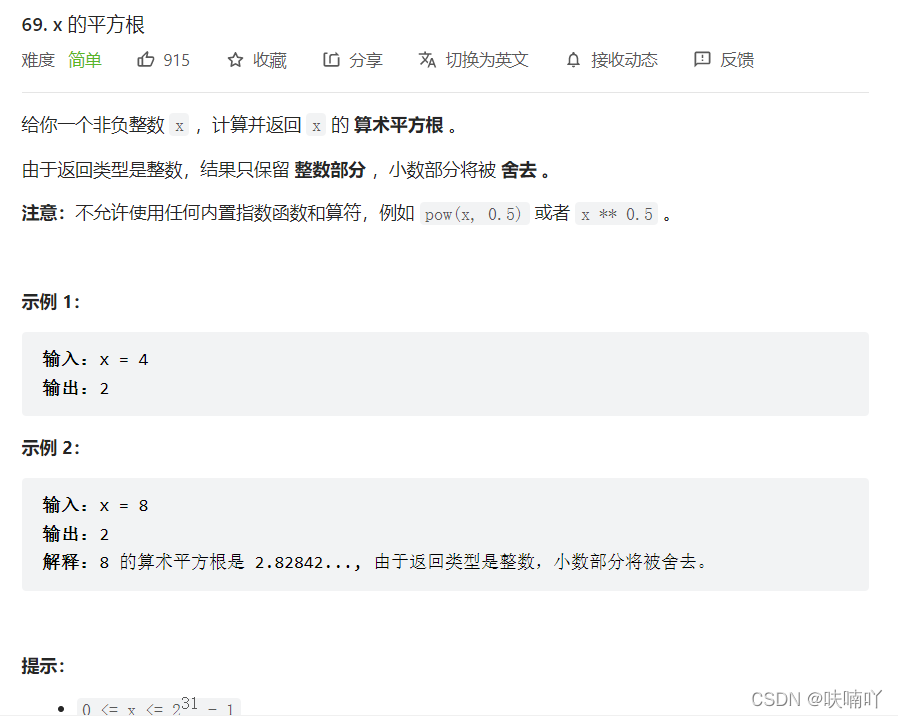
思路:
依旧是,在[0,x]中找到一个数,k,只要满足kk <= x,
那么就可以说明当kk = x,k就是x的算术平方根;
当k*k<x,那么说明k可能是x的算术平方根(题目的要求小数点的数会被舍掉,所以说,k * k< x是有可能成为x的算术平方根的值);
当k > x那么直接pass掉;
由于这个又是在[0,x]升序查找,所以说:我们还是用二分查找算法解决;
代码
class Solution {
public:
int mySqrt(int x) {
//在[0,x]中不断试数,算出结果
//找到一个数k,满足k*k <= x即可
int left = 0;
int right = x;
int ret = -1; //保存结果的值
while(left <=right)
{
int middle = left + ((right-left)>>1);
if((long long)middle*middle<=x)
{
ret = middle;//由于<的情况也有可能找到ret,所以就保存该middle值
left = middle+1;
}
else
{
right = middle -1;
}
}
return ret;
}
};
3.3 搜索插入位置
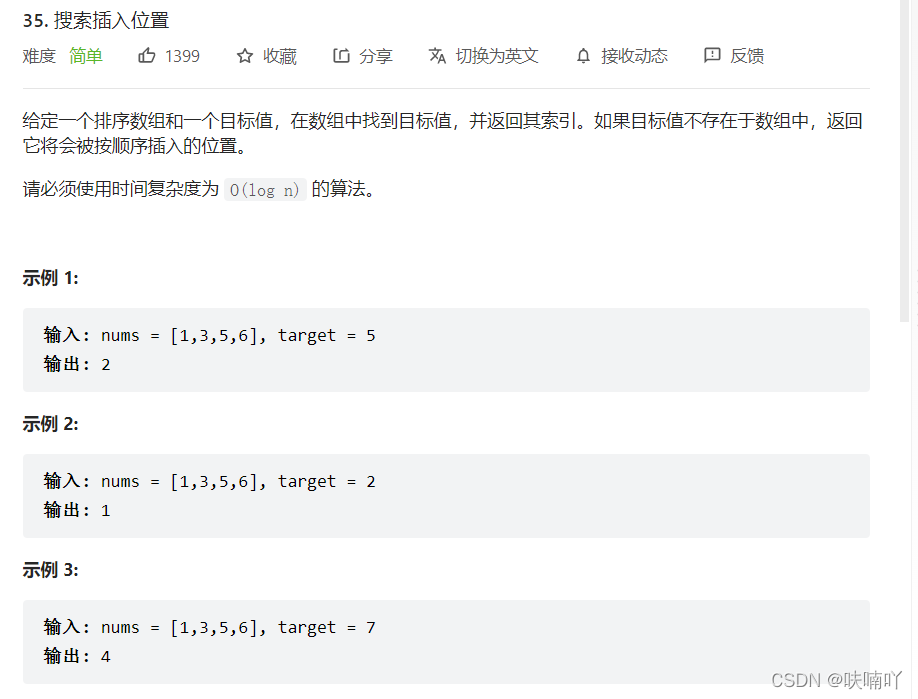
有序的数据,毫无疑问,直接二分算法:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
//注意我这里是左闭右开的区间
int left = 0;
int right = nums.size();
while(left < right)
{
int middle = left +((right - left)>>1);
if(target<nums[middle])
{
right = middle;
}
else if ( target > nums[middle])
{
left = middle +1;
}
else
{
return middle;
}
}
//1.头插,比[1,2,3],插入0,
//2.尾插,比如[1,2,3]插入4,
//3.插中间,比如[1,2,4]插入3
return right;
}
};
3.4 在排序数组中查找元素的第一个和最后一个位置
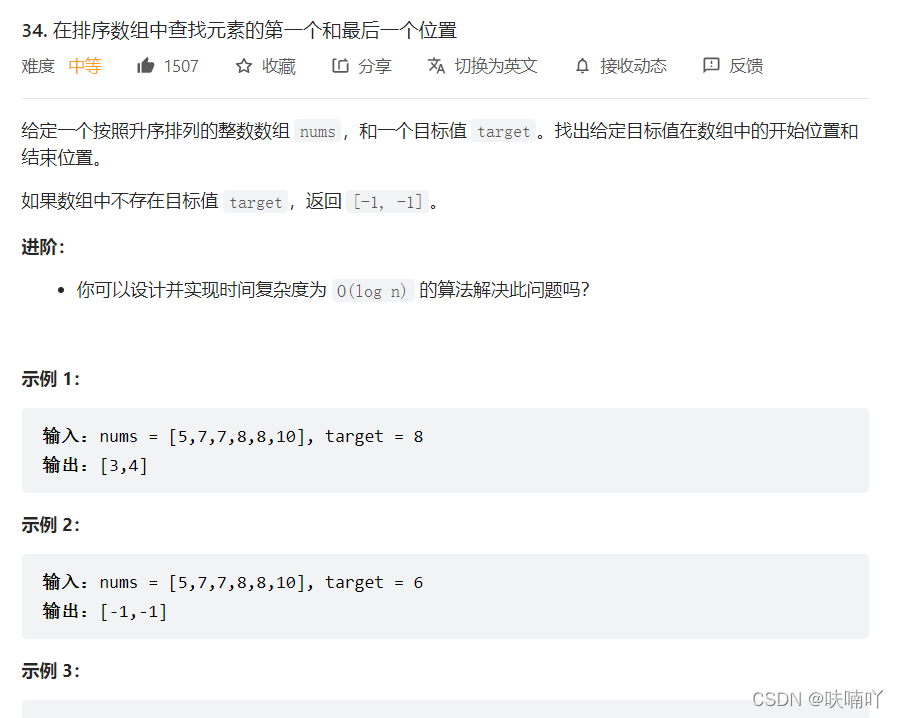
二分算法不多说:
主要是我们要如何找到第一个数位置,和最后一个数位置:
首先我们得清楚,当我们找第一个数位置时候,需要把一种情况:即二分查找时候,target == nums[middle]时候得条件,也需要让 right = middle -1;的操作,这样才可以把最后一个数的位置给避开;
反之亦然,也就是说,擦或者最后一个数时候,也是这样操作;
代码:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
//先找到第一个值的最左下标
int left = LeftIndex(nums,target);
//在找最后一个值的最右下标
int right = RightIndex(nums,target);
if(right < left )
return vector<int>{-1,-1};
//right >=left,
//大于情况就是正常的有多个相同的目标值,
//等于的情况就是数组只有一个数
return vector<int>{left,right};
}
int LeftIndex (vector<int>&nums ,int target)
{
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int middle = left + ((right - left) >> 1);
if(target <= nums[middle])
right = middle - 1;
else
left = middle + 1;
}
//退出循环后,下标区间为【right,left】,而left就是要找的值
//或者退出循环后,left不是要找的值如【1,7,8,9,10】找 8,
// 退出循环后下标位置在left = 2; right = 1
return left;
}
int RightIndex (vector<int>&nums,int target)
{
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int middle = left +( (right - left) >> 1);
if(target >=nums[middle]) //大于等于的条件就继续移动左下标,直到退出循环
left = middle + 1;
else
right = middle - 1;
}
//退出循环后,下标区间为【right,left】,而right就是要找的值
return right;
}
};