[数据结构与算法]堆排序算法

前置知识：

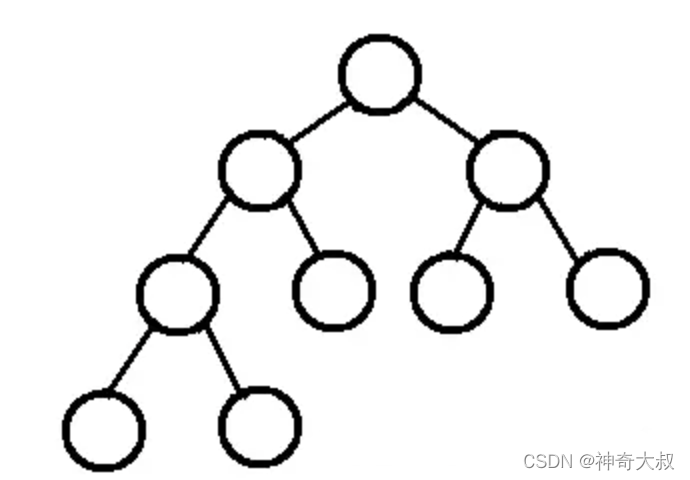
• 完全二叉树：深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h 层所有的结点都连续集中在最左边（即从最左边开始排列），从上到下，从左到右，节点序号和节点个数一一对应

• 满二叉树：除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树

  • 故满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树
    

完全二叉树的特性

• 完全二叉树可以用数组进行存储
  • 如果我们把根节点存放在位置 i=1 的位置，则它的左子节点位置为 2i = 2 ，右子节点位置为 2i+1 = 3 。
  • 如果我们选取 B 节点 i=2 ，则它父节点为 i/2 = 1 ，左子节点 2i=4 ，右子节点 2i+1=5 。
• 所有的节点都满足这三种关系
  • 位置为 i 的节点，它的父节点位置为 i/2
  • 它的左子节点 2i
  • 它的右子节点 2i+1
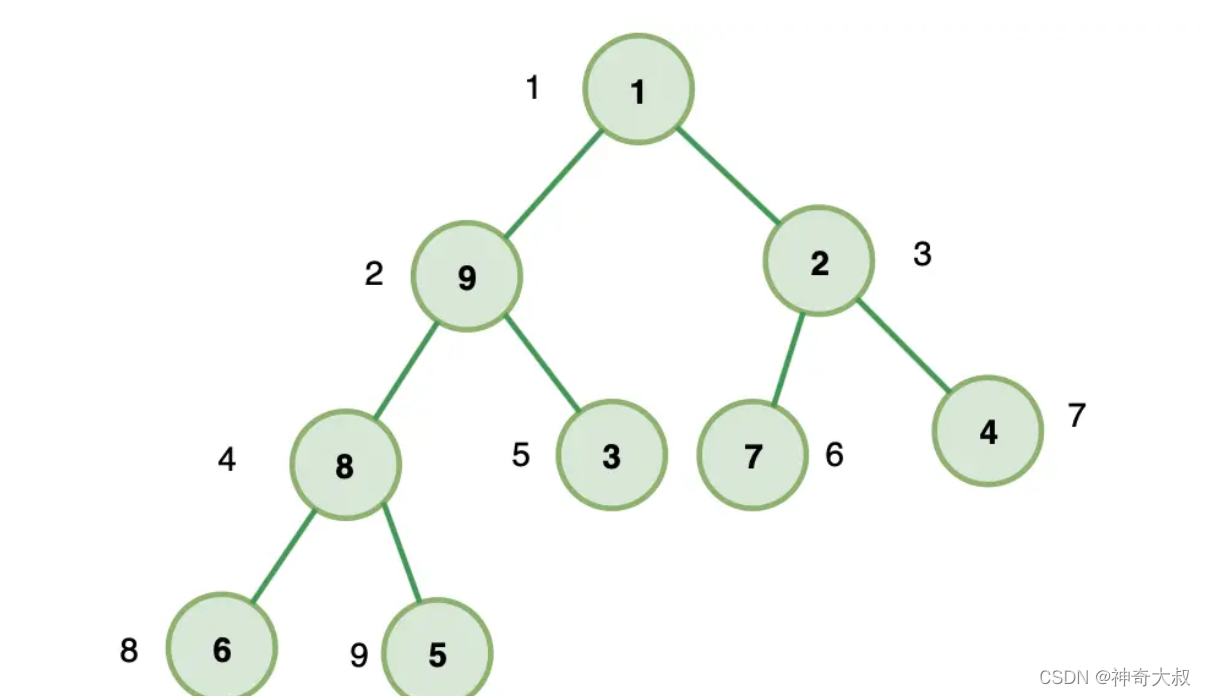
• 下面的完全二叉树用数组表示为，[1,9,2,8,3,7,4,6,5]

堆

• 堆是一个完全二叉树，分为大顶堆和小顶堆

• 大顶堆：堆上的任意节点值都必须大于等于其左右子节点值

  • 故大顶堆的堆顶一定是最大的数
    

• 小顶堆：堆上的任意节点值都必须小于等于其左右子节点值

  • 故小顶堆的堆顶一定是最小的数
    

建堆：

• 如上所知，堆是个完全二叉树，那么堆其实可以用一个数组表示，给定一个节点的下标 i （i从1开始） ，那么它的父节点一定为 A[i/2] ，左子节点为 A[2i] ，右子节点为 A[2i+1]

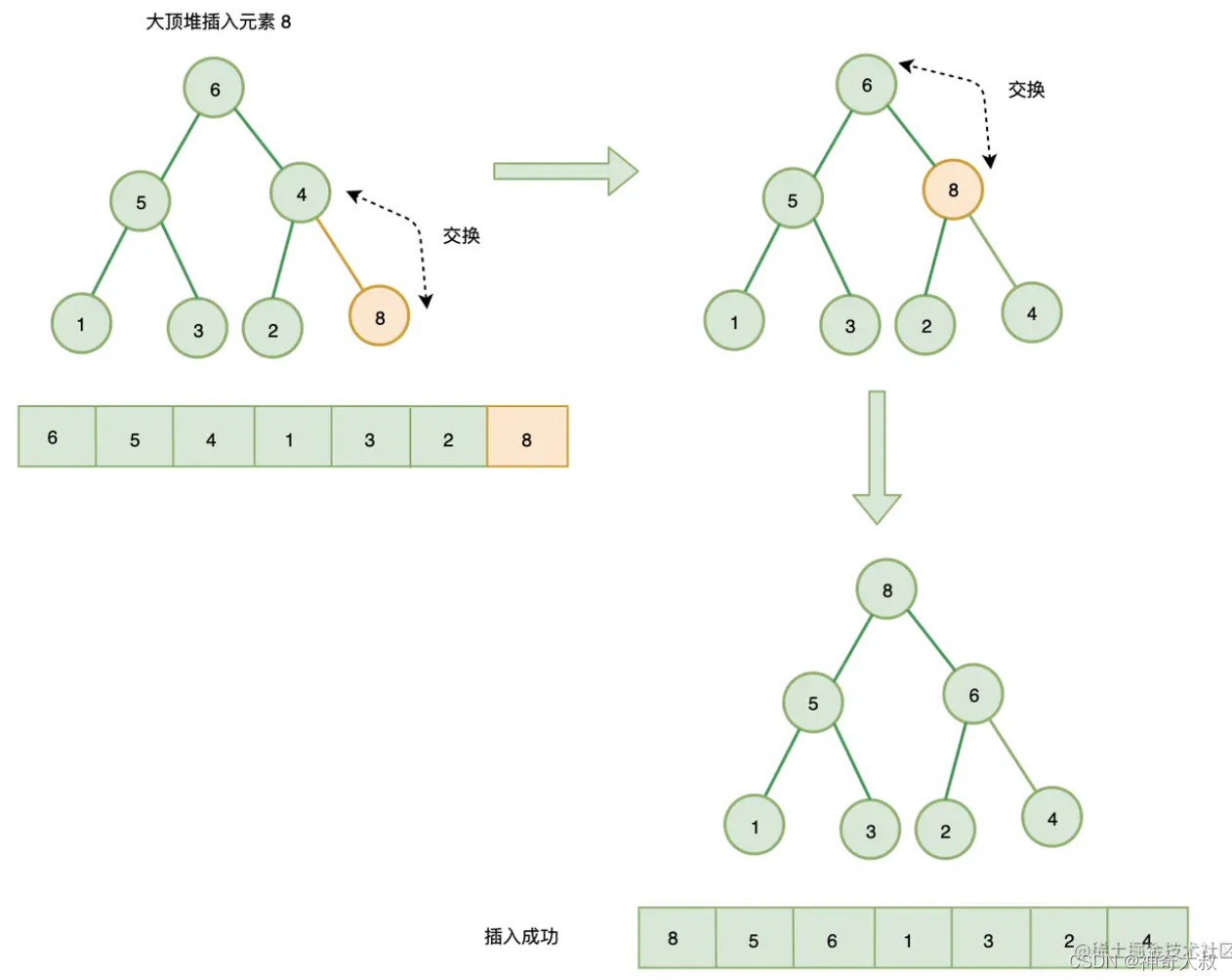
插入式建堆：这里以大顶堆为例

• 将节点插入到队尾
• 自下往上堆化： 将插入节点与其父节点比较，如果插入节点大于父节点（大顶堆）或插入节点小于父节点（小顶堆），则插入节点与父节点调整位置
• 一直重复上一步，直到不需要交换或交换到根节点，此时插入完成。
  

let  items=[];

function insert(key) {
    items.push(key)
    // 获取尾插入节点索引
    let i = items.length-1 
    while (i/2 > 0 && items[i] > items[Math.ceil(i/2)-1]) {   //当前元素索引取 Math.ceil(i/2)-1是因为，1和2的父元素索引都是0;
        swap(items, i, Math.ceil(i/2)-1); // 交换 
        //交换后，再比较交换位置后的节点与父节点的大小，如此反复
        i = Math.ceil(i/2)-1; 
    }
}  
function swap(items, i, j) {
    let temp = items[i]
    items[i] = items[j]
    items[j] = temp
}

insert(6);
insert(5);
insert(4);
insert(1);
insert(3);
insert(2);
insert(8);

console.log(items) //8 5 6 1 3 2 4

原地建堆（堆化）：这里以小顶堆为例

• 自下而上式堆化 ：将节点与其父节点比较，如果节点大于父节点（大顶堆）或节点小于父节点（小顶堆），则节点与父节点调整位置
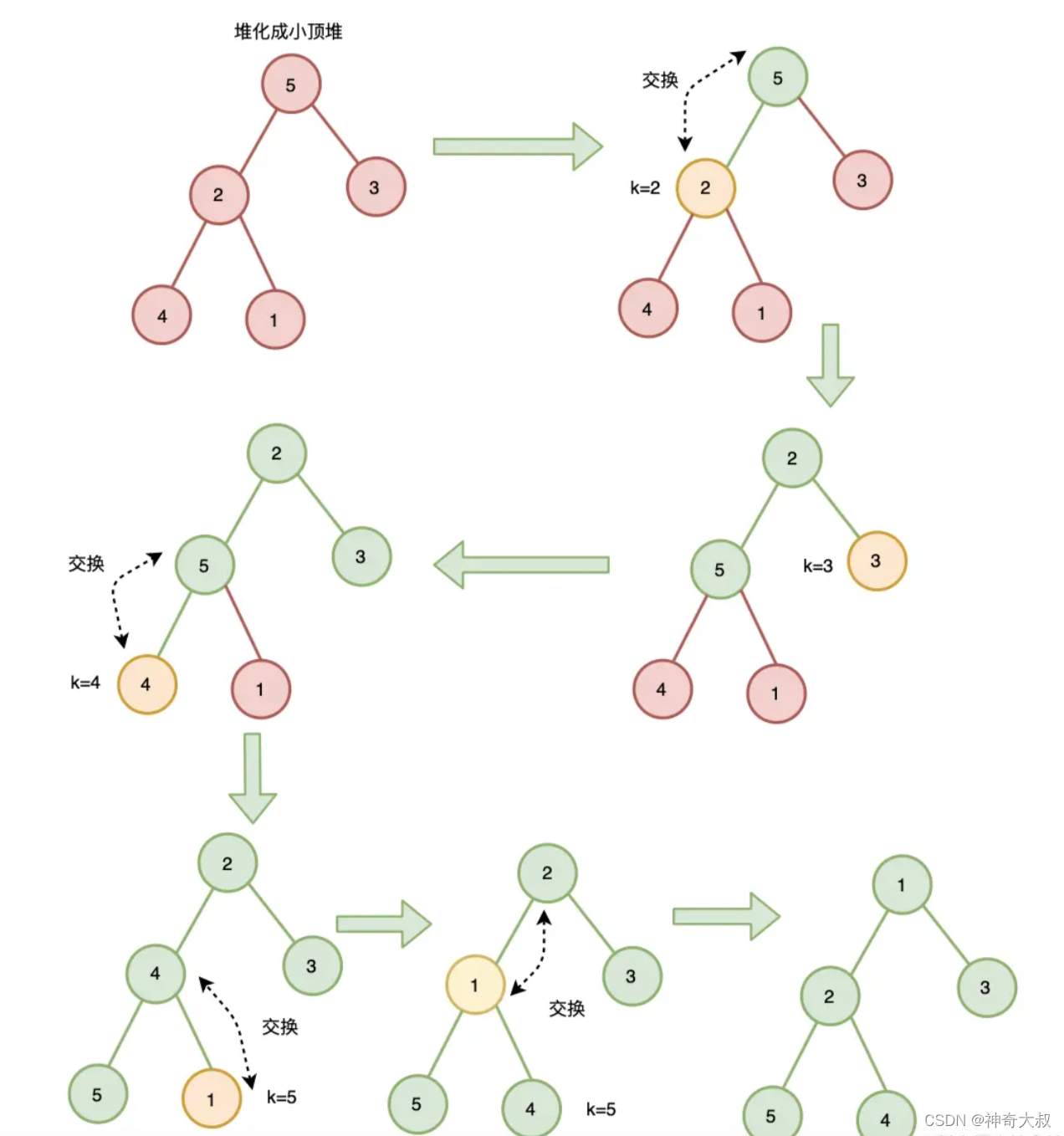
  • 从第一个元素开始，每遍历一个元素，就和它的父元素进行比较交换，类似插入式建堆的做法
    

//原地建堆
function buildHeap(items, heapSize) {
    while(heapSize < items.length-1) {
        heapSize ++
        heapify(items, heapSize)
    }
}

function heapify(items, i) {
    // 自下而上式堆化
    当前元素索引取 Math.ceil(i/2)-1是因为，1和2的父元素索引都是0;
    while (i/2 > 0 && items[i] <items[Math.ceil(i/2)-1]) {  
        swap(items, i, Math.ceil(i/2)-1); // 交换 
        i = Math.ceil(i/2)-1; 
    }
}  

function swap(items, i, j) {
    let temp = items[i]
    items[i] = items[j]
    items[j] = temp
}

// 测试
var items2 = [5,2,3,4,1]
buildHeap(items2, 0)
console.log(items2) // 1 2 3 5 4

• 自上往下式堆化 ：从最后一个非叶子结点开始与其左右子节点比较，如果存在左右子节点大于该节点（大顶堆）或小于该节点（小顶堆），则将子节点的最大值（大顶堆）或最小值（小顶堆）与之交换
  • 每交换一次，还要继续比较交换后节点与其子左右节点的大小，因为不能保证上一部交换的节点是以当前节点为根的树中最大或最小的
  • 需要从最后一个非叶子节点开始，而非最后一个节点，因为完全二叉树的原因，最后一个非叶子结点就包含了最后两个或一个节点，从而能保证最后一个非叶子结点交换后是有序的（即是以当前节点为根的树，根为最大或最小），然后从最后一个非叶子结点的序号-1的节点开始遍历交换直到序号为0，因为完全二叉树的结构，从最后一个非叶子结点开始，令其序号不断-1，就能从整个树的左右子树的左右两边最底层开始不断往上提升，最终比较整个树的根节点和其两个子节点
  • 最后一个非叶子节点公式：（n-1）/2

// 原地建堆
// items: 原始序列
function buildHeap(items) {
    let heapSize = items.length
    // 从最后一个非叶子节点开始，然后遍历到序号为0的节点为止，使得完全二叉树能从左右两个子树的最底层开始往上整合，直到根节点
    for (let i = Math.floor(heapSize/2); i >= 1; --i) {    
        heapify(items, heapSize, i);  
    }
}
function heapify(items, heapSize, i) {
    // 当前节点比较交换后，还要继续比较交换后节点和其子左右节点大小，以保证当前节点的子树都满足大顶堆或小顶堆的结构
    while (true) {
        var maxIndex = i;
        if(2*i <= heapSize && items[i] > items[i*2] ) {
            maxIndex = i*2;
        }
        if(2*i+1 <= heapSize && items[maxIndex] > items[i*2+1] ) {
            maxIndex = i*2+1;
        }
        if (maxIndex === i) break;
        swap(items, i, maxIndex); // 交换 
        i = maxIndex; 
    }
}  
function swap(items, i, j) {
    let temp = items[i]
    items[i] = items[j]
    items[j] = temp
}

// 测试
var items = [,5, 2, 3, 4, 1]
buildHeap(items, items.length - 1)
console.log(items)
// [empty, 1, 2, 3, 4, 5]

二叉堆新增节点（小顶堆为例）

• 将新元素插入到数组末尾
• 新增节点和上面的插入建堆原理一致，不断向上与父节点比较
  
  

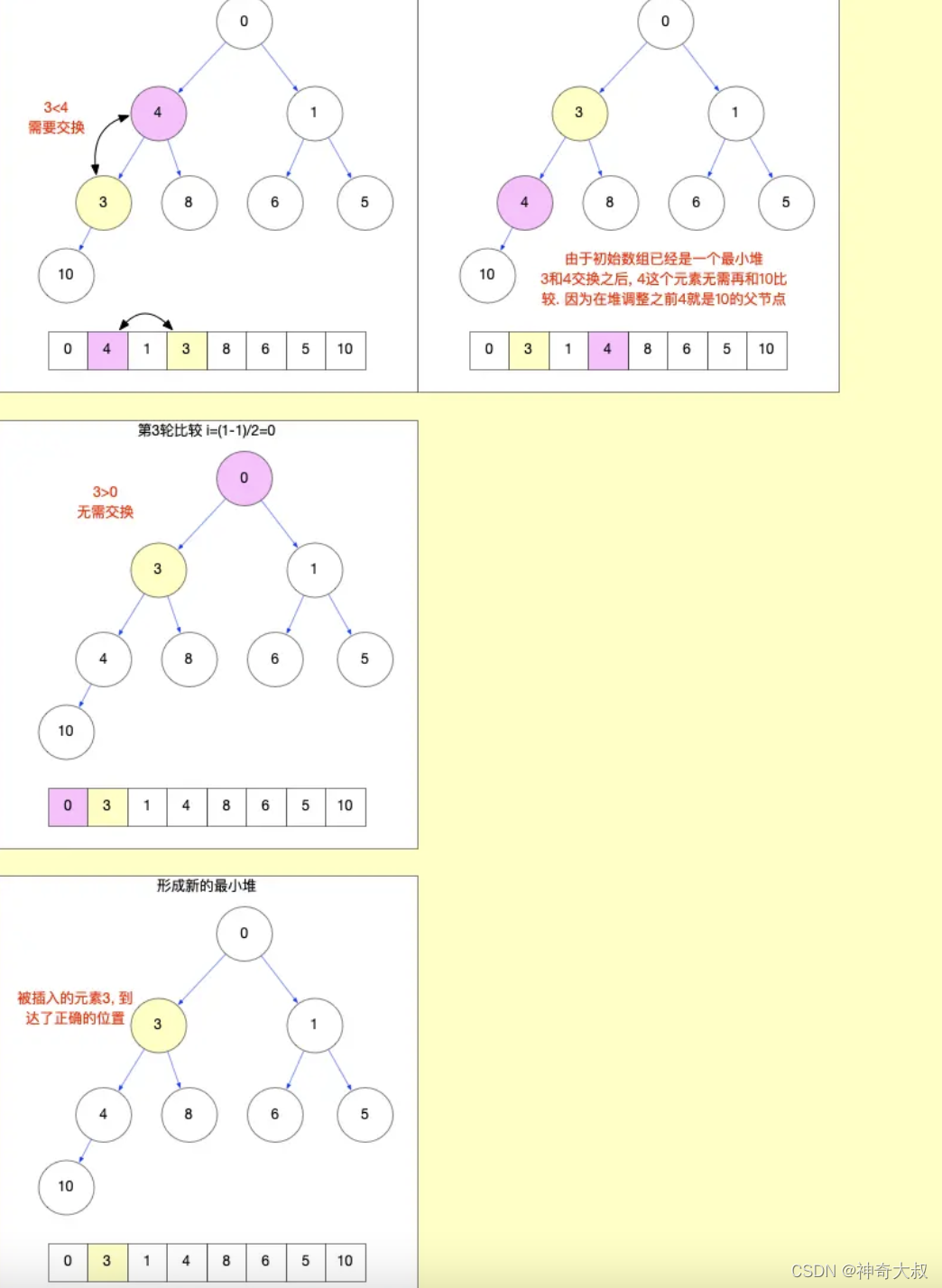
二叉堆提取或删除节点（小顶堆为例）

• 提取后重新放置的节点，和最小的子节点相比是因为最小子节点若交换到父节点，较小的节点一定比较大的节点小，不用再考虑较小节点是否还需要交换位置，否则若交换较大的节点，较大的节点还需要和较小的节点交换位置再进行排序

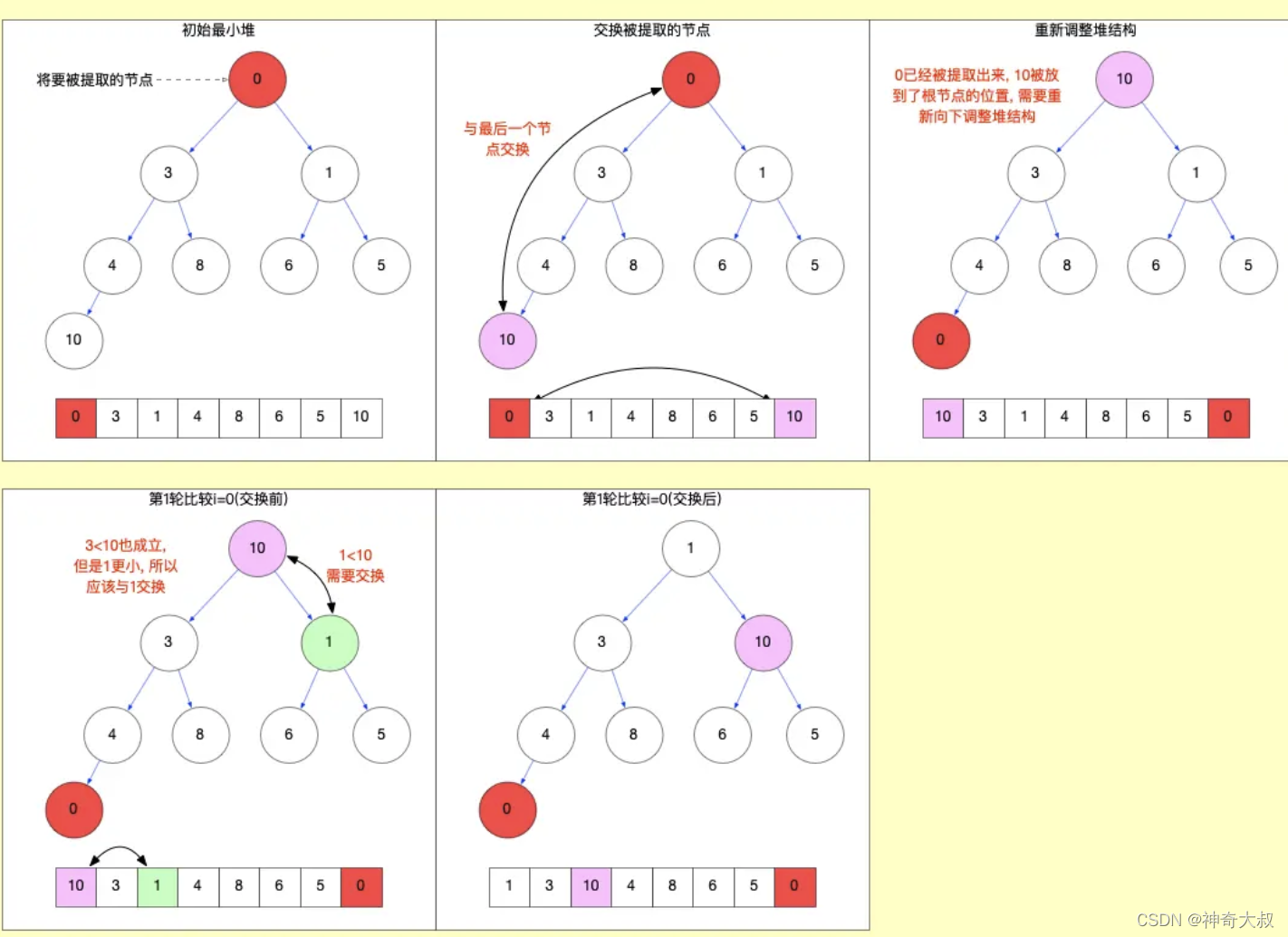
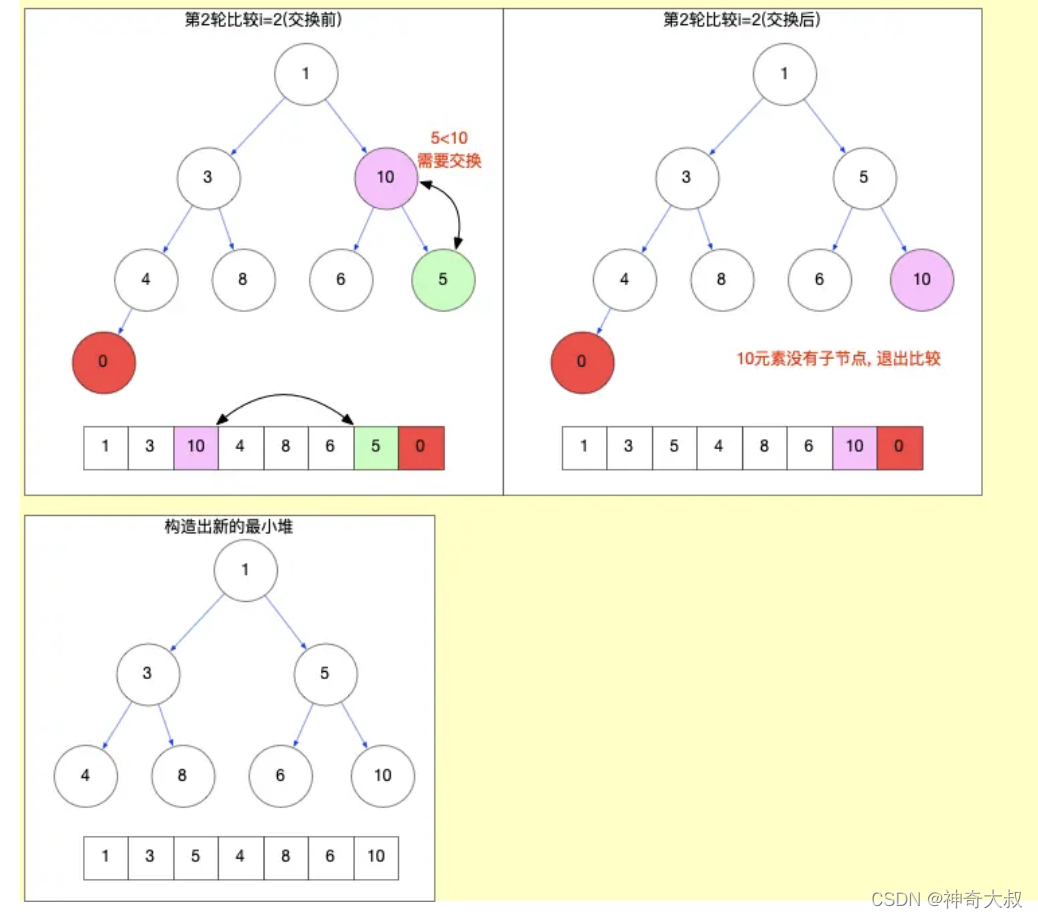
堆排序：

• 如上通过大顶堆和小顶堆知道，当前堆的根节点一定是整个树的最大或最小的值
• 将根结点位置和最后一个节点位置交换，即对应数组中，将根结点和数组尾元素交换位置，然后每次将数组长度-1，让数组剩余元素再进行堆化，反复执行该操作，最终达成整个数组有序
• 可知，整个建堆过程和堆排序，都可以看做一个选择排序，整体时间复杂度是 O(nlogn)