文章目录
一、B树基础知识
B是Balance平衡的意思,B树的所有叶子节点都在同一层。m阶-平衡树 (一个节点有m个地址域,m-1个数据域),主要应用在文件索引系统。
AVL树:二阶平衡树。一个节点有2个地址域,1个数据域。(左右孩子的高度差是1,0,-1)
m阶B-树:最多有m个地址域(即m个孩子),m-1个数据域。除根节点和叶子节点外,其他节点的孩子至少有一半个数的孩子(指针域)(比如说有5个孩子,ceil(5/2)=3,至少有3个孩子)。
为什么说除根节点和叶子节点外,其他节点的孩子至少有一半个数的指针域? 因为数据达到m了,节点就要进行分裂,提出一个数据成为父节点。若m是偶数,两侧数据个数分别是m/2和m/2-1,分别成为一个独立的节点,对于只有m/2-1个数据的节点来说,指针域就有m/2个,也就是ceil(m/2)
对于5阶B树来说,除根节点之外的节点的数据的个数,不能到达5,到达5的话节点就要分裂。内部节点和叶子节点范围能存储的数据范围是 [ceil(m/2)-1, m - 1],而指针域始终比数据域多一个
二、B树的插入过程

按C、N、G、A、H、E、K、Q、M、F、W、L、T、Z、D、P、R、X、Y、S的顺序构造一棵5阶B树,详细过程如下:
分析:5阶的B树,非根节点数据个数在区间[2,4]内,每个节点最多有5个指针域,除根节点和叶子节点外,其他节点至少有2个数据,3个指针域。



对于B树来说,分裂都是向上分裂的,是非常平衡的。所有的叶子节点都在同一层,且满足搜索树的性质
三、B树的删除过程
删除以及调整的过程如下:

依次删除H、T、R、E
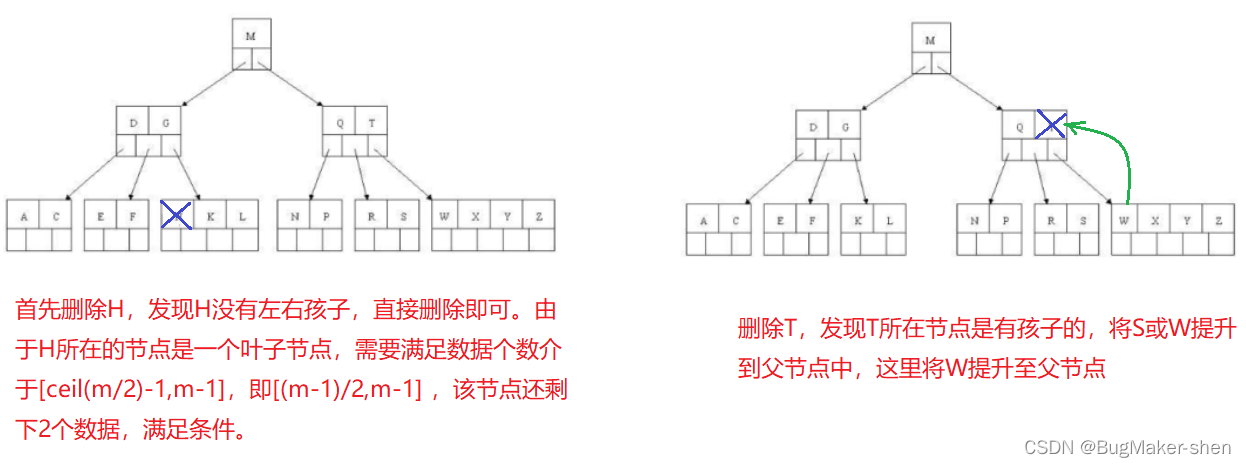


四、B树的磁盘IO优势和搜索效率
Windows和linux的文件搜索,以及数据库的索引,都用到了B+树结构(修改原始B树结构可得到)
在系统中的数据搜索中:大量的数据都是存储在磁盘上的。为了增加系统的搜索速度,我们一般会给数据创建索引。而所谓的创建索引,就是给数据进行排序,然后进行数据搜索就更加快速。
如果想对磁盘上存储的数据进行快速搜索查找需要解决两个问题:
- 更少的磁盘I/O
- 更快的搜索速度、算法
我们在这里采用m阶平衡树(节点分裂调平衡)。红黑树不是平衡树,是二阶非平衡树。AVL树是二阶平衡树(节点旋转调平衡),左右孩子高度差不超过1。
对比AVL树以及B树的效率
操作系统管理内存都是按页面page(4K)分配,管理磁盘是按块block(16K)分配。我们的文件在磁盘存储,从磁盘读1个文件,读4个字节,实际上,操作系统从磁盘是按block(16K)来读取的。
磁盘的最小单位是扇区,一个扇区大小为512字节,一个block是16K,16K除以512就是扇区的个数。
假如现在从磁盘读取10000000个索引,构建索引树,对比B树和AVL树的花费:

如果用AVL树(相当于2阶B树)构建索引树来存储10000000个索引,需要24层。一个节点就是存储着一个索引数据,最差情况就是每个节点的数据都不在一个磁盘block上,一个节点对应一个磁盘I/O,我们查找一个数据最多查找24次,即最多需要24次磁盘I/O。
同理,使用300阶B树,查找一次数据最多找3层,花费3次磁盘I/O。
故在构建索引树的时候,我们更多的使用B树
五、B+树理论部分

磁盘上读数据,是按照block读取的。图中是3阶的,2个数据域,3个地址域,图中的数字代表索引项(例如学号作为索引)
数据都在磁盘上,花费更少的磁盘I/O才是最重要的。
我们看B树的每个节点存储的不仅仅是关键字(索引项),还存储着红色的点,这个红色的点代表索引项对应的记录,就是一行的数据。比如我们读取学号为17的数据,那就花费1次磁盘I/O;读取学号为99的数据,那就花费3次磁盘I/O。

m阶B+树和m阶B树的区别
B+树是B树的变形树
- 所有的叶子节点包含全部的关键字信息,及指向含有这些关键字记录的指针
- 非叶子节点相当于是叶子节点的索引,不存储数据,叶子节点用于存储关键字以及数据
- 索引项和数据都出现在叶子节点中,搜索每一个数据所花费的磁盘I/O都是一样的
- 所有的叶子节点被串在一条有序的链表当中,当我们在进行区间查找的时候(where id > 1 and id < 10),我们不用遍历复杂的B+树,我们直接遍历叶子节点组成的链表即可
- B+树存储的索引值是有重复的,且每个节点中的关键字是有序的
B+树比B树更适合操作系统的文件索引和数据库索引的原因

B+树非叶子节点只存索引项,相对于B树就不存数据地址,所以相同大小的节点存的关键字更多,花费的磁盘I/O就少,找的就快。而且由于每个节点存储的索引多了,树的层数更低!


B树的一个节点存储了8个索引项和8个具体数据的指针地址,一共(8+8)*2=32B,需要用到两个block(磁盘块)存储一个节点。而B+树的非叶子节点只存储所索引项,而不存储具体数据的指针地址,所以B+树的一个节点16字节可以全部用来存储索引项,一个block就可以存储一个B+树的节点。
B树和B+树的区别

六、B*树
B*树是B+树的变体,在B+树的内部节点(非根和非叶子节点)再增加指向兄弟节点的指针

