程序内功篇四--栈
一、栈的原理
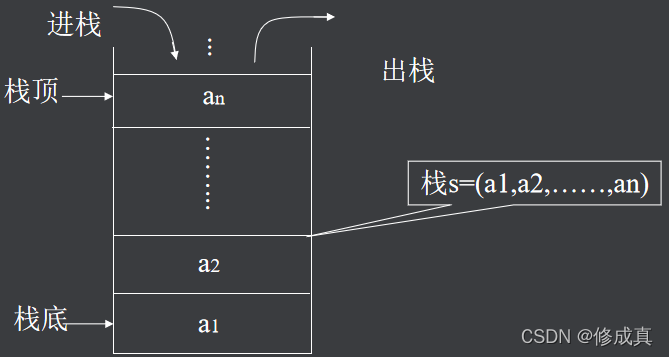
栈是限制在一端进行插入操作和删除操作的线性表(俗称堆栈)
允许进行操作的一端称为“
栈顶”
另一固定端称为“
栈底”
当栈中没有元素时称为“
空栈”。栈的特点 :后进先出(LIFO)。
二、顺序栈的实现
有关顺序表的原理及实现看这篇文章:
【数据结构与算法】程序内功篇二–线性顺序表
1、顺序栈原理
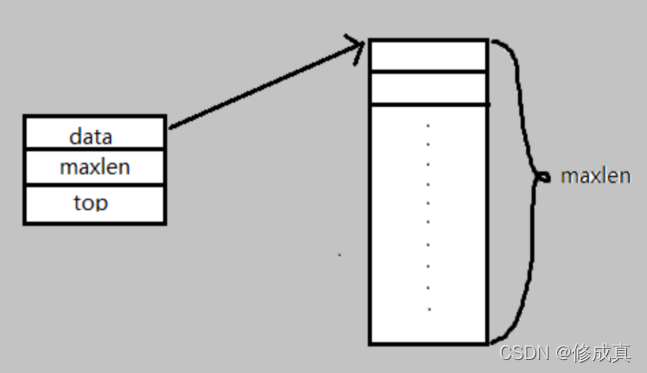
它是
顺序表的一种,具有顺序表同样的存储结构,由数组定义,配合用数组下标表示的栈顶指针top(相对指针)完成各种操作。
结构体定义:
typedef int data_t ; /*定义栈中数据元素的数据类型*/
typedef struct
{
data_t *data ; /*用指针指向栈的存储空间*/
int maxlen; /*当前栈的最大元素个数*/
int top ; /*指示栈顶位置(数组下标)的变量*/
} sqstack; /*顺序栈类型定义*/
2、栈的创建
/**
* @description: 顺序栈的创建
* @param {int} len -用户规定的栈长
* @return {sqstack-栈顶指针}
*/
sqstack* stack_create(int len) {
sqstack * s;
if ((s =(sqstack *)malloc(sizeof(sqstack))) == NULL)
{
printf("malloc sqstack failed\n");
return NULL;
}
if ((s->data = (data_t *)malloc(len * sizeof(data_t)))==NULL)
{
printf("malloc data failed\n");
free(s);
return NULL;
}
memset(s->data, 0, len*sizeof(data_t));
s->maxlen = len;
s->top = -1;
return s;
}
3、顺序栈进栈
/**
* @description: 进栈
* @param {sqstack* } s-栈顶指针
* @param {data_t} value-进栈的值
* @return {-1-函数失败,0-函数成功}
*/
int stack_push(sqstack *s, data_t value)
{
if (s == NULL) {
printf("s is NULL\n");
return -1;
}
if (s->top == s->maxlen-1)
{
printf("stack is full\n");
return -1;
}
s->top++;
s->data[s->top] = value;
return 0;
}
4、顺序栈出栈
/**
* @description: 出栈
* @param {sqstack*} s-栈顶指针
* @return {栈顶的值}
*/
data_t stack_pop(sqstack *s) {
s->top--;
return (s->data[s->top+1]);
}
5、顺序栈删除
/**
* @description: 顺序栈删除
* @param {sqstack*} s-栈顶指针
* @return {-1-函数失败,0-函数成功}
*/
int stack_free(sqstack *s) {
if (s == NULL) {
printf("s is NULL\n");
return -1;
}
if (s->data != NULL)
free(s->data);
free(s);
return 0;
}
6、清空栈与是否清空栈
/**
* @description: 栈清空
* @param {sqstack*} s-栈顶指针
* @return {-1-函数失败,0-函数成功}
*/
int stack_clear(sqstack *s) {
if (s == NULL) {
printf("s is NULL\n");
return -1;
}
s->top = -1;
return 0;
}
/**
* @description: 判断栈是否为空
* @param {sqstack*} s-栈顶指针
* @return {-1-函数失败,1-栈为空,0-栈不为空}
*/
int stack_empty(sqstack *s)
{
if (s == NULL) {
printf("s is NULL\n");
return -1;
}
return (s->top == -1 ? 1 : 0);
}
三、链表栈的实现
有关链表的原理及实现请看这篇文章:
【数据结构与算法】程序内功篇三–单链表
1、栈的单链表实现
插入操作和删除操作均在链表头部进行,链表尾部就是栈底,栈顶指针就是头指针。
结点定义:
typedef int data_t ; /*定义栈中数据元素数据类型*/
typedef struct node {
data_t data ; /*数据域*/
struct node *next ; /*链接指针域*/
}stacklist,*stacklink; /*链栈类型定义*/
2、创建空栈
/**
* @description: 单链表栈的创建
* @param {*}
* @return {栈顶指针}
*/
stacklink stacklist_create()
{
stacklink top;
if((top = (stacklink)malloc(sizeof(stacklist))) == NULL)
{
#if DEBUG
printf("stacklist create error!\n");
#endif
return 0;
}
top->data = 0;
top->next = NULL;
return top;
}
3、入栈
/**
* @description: 入栈-头插发
* @param {stacklink} top-栈顶指针
* @param {data_t} value-入栈的值
* @return {0-函数成功,1-函数失败}
*/
int stacklist_top_insert(stacklink top, data_t value)
{
stacklink sl;
if(top == NULL)
{
#if DEBUG
printf("top is NULL!\n");
#endif
return 0;
}
if((sl = (stacklink)malloc(sizeof(stacklist))) == NULL)
{
#if DEBUG
printf("stacklist create error!\n");
#endif
return 0;
}
sl->data = value;
sl->next = top->next;
top->next = sl;
return 1;
}
4、出栈
/**
* @description: 出栈
* @param {stacklink} top-栈顶指针
* @return {0-函数成功,1-函数失败}
*/
int stacklist_out(stacklink top)
{
stacklink sl;
int value;
if(top == NULL)
{
#if DEBUG
printf("top is NULL!\n");
#endif
return 0;
}
if(top->next == NULL)
{
#if DEBUG
printf("stacklist is empty!\n");
#endif
return 0;
}
sl = top->next;
top->next = sl->next;
value = sl->data;
free(sl);
return value;
}
5、删除链表栈
/**
* @description: 栈删除
* @param {stacklink} top-栈顶指针
* @return {0-函数成功,1-函数失败}
*/
int stacklist_free(stacklink top)
{
stacklink sl = top;
if(top == NULL)
{
#if DEBUG
printf("top is NULL!\n");
#endif
return 0;
}
while(top)
{
top = top->next;
free(sl);
sl = top;
}
return 1;
}
6、判断是否为空栈
/**
* @description: 判断是否为空表
* @param {stacklink} top-栈顶指针
* @return {-1-函数失败,1-为空栈,0-不为空栈}
*/
int stacklist_empty(stacklink top)
{
if(top == NULL)
{
#if DEBUG
printf("top is NULL!\n");
#endif
return -1;
}
return (top->next == NULL? 1:0);
}
四、栈的应用
建立操作数栈和运算符栈。运算符有优先级。
①
自左至右扫描表达式,凡是遇到操作数一律进操作数栈。
②当遇到运算符时,如果它的优先级比运算符栈栈顶元素的优先级高就进栈。反之,取出栈顶运算符和操作数栈栈顶的连续两个操作数进行运算,并将结果存入操作数栈,然后继续比较该运算符与栈顶运算符的优先级。
③左括号一律进运算符栈,右括号一律不进运算符栈,取出运算符栈顶运算符和操作数栈顶的两个操作数进行运算,并将结果压入操作数栈,直到取出左括号为止。
例如:计算 ( 4+8 )×2-3 ;
操作数栈 :4 8 | 12 2 |24 3 |21
运算符栈 :( + |× |- |

想要基本实现程序的点击下面的链接免费的:
栈的基本C程序
到这里就结束啦!