[数据结构与算法]数据结构 --- C语言实现哈夫曼树

?哈夫曼树的结构体描述?

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#define MAX 100
typedef struct huffmanTreeNode 
{
	int key;                               //键--->出现的频率
    //char data;                           //当前频率对应的字符--->方便做解码
	struct huffmanTreeNode* parentNode;    //记录树的父节点--->方便连接操作
	struct huffmanTreeNode* LChild;        //左子树节点
	struct huffmanTreeNode* RChild;        //右子树节点
}NODE,*LPNODE,*LPTREE;

?准备一个堆存放节点--->堆的结构体描述

//小顶堆
typedef struct heap
{
	int sizeHeap;        //堆中元素个数
	LPNODE* heapData;    //存储LPNODE的指针--->存放多个一级指针用二级指针
}HEAP,*LPHEAP;

?创建堆--->数组实现 用结构体指针表示堆?

LPHEAP createHeap() 
{
	LPHEAP heap = (LPHEAP)malloc(sizeof(HEAP));
	assert(heap);
    //给数据做初始化
	heap->sizeHeap = 0;
	heap->heapData = (LPNODE*)malloc(sizeof(LPNODE) * MAX);
	return heap;
}

?万金油函数

int size(LPHEAP heap) 
{
	return heap->sizeHeap;
}
//判断堆是否为空
int empty(LPHEAP heap) 
{
	return heap->sizeHeap == 0;
}

?调整堆--->向上渗透

//要调整的堆 当前元素的下标
void moveTocorrectPos(LPHEAP heap, int curPos)
{
	while (curPos > 1)                       //>1 一直往上冒渗透到下标[1]的位置
	{
		LPNODE min = heap->heapData[curPos]; //假设当前位置是最小的 与上面节点的值相比较
		int parentIndex = curPos / 2;        //求出父节点的下标
		if (min->key < heap->heapData[parentIndex]->key) //比较两个键 当前的键<父节点中的键就向上渗透
		{
			heap->heapData[curPos] = heap->heapData[parentIndex]; //交换父节点和子节点的值
			heap->heapData[parentIndex] = min;                    
			curPos = parentIndex;                                 //下标向1靠近
		}
		else                                 //大于的情况说明放在了合适的位置 不用往上冒
		{
			break;
		}
	}
}

?堆的插入

//要插入的堆 要插入的数据
void insertHeap(LPHEAP heap, LPNODE data) 
{
    //存数据:直接放在当前数组后面即可 前置++第一个位置不存数据 存第1个元素放在[1]下标中
	heap->heapData[++heap->sizeHeap] = data;
    //向上渗透 调整堆
	moveTocorrectPos(heap, heap->sizeHeap);
}

?出堆--->向下渗透

//要出的堆 返回节点
LPNODE popHeap(LPHEAP heap) 
{
	LPNODE min = heap->heapData[1];             //第一个元素肯定是最小的 下标为[1]的元素
	int curPos = 1;
	int childIndex = curPos * 2;
	while (childIndex <= heap->sizeHeap) 
	{
		LPNODE temp = heap->heapData[childIndex];
		//横向比较找最小值 只要比较横向的2个值 childPos + 1为右边的值
		if (childIndex + 1 <= heap->sizeHeap && temp->key > heap->heapData[childIndex + 1]->key) 
		{
			temp = heap->heapData[++childIndex]; //如果左边的值>边的值 需要往右走
		}
		//向下渗透
		heap->heapData[curPos] = temp;           //如果往左边走 接着往下找即可
		curPos = childIndex;                     //当前pos往下走
		childIndex *= 2;
	}
	heap->heapData[curPos] = heap->heapData[heap->sizeHeap]; //找到最终交换的元素
	moveTocorrectPos(heap, curPos);              //存在不满足规则的情况做调整
	--heap->sizeHeap;
	return min;
}

?创建哈夫曼树的节点

//传入关键字
LPNODE createNode(int key) 
{
    //创建节点
	LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
	assert(newNode);
    //给数据做初始化
	newNode->key = key;
	newNode->LChild = NULL;        //左右子树指针都指向NULL
	newNode->RChild = NULL;
	newNode->parentNode = NULL;    //单一节点没有父节点,父节点也指向NULL
	return newNode;
}

?构建哈夫曼子树的节点 从堆中挑两个最小的节点构成新的节点

//传入两个节点
LPNODE createhuffmanNode(LPNODE first, LPNODE second) 
{
	LPNODE parentNode = createNode(first->key + second->key);   //父节点的关键字==两个节点的关键字相加
    //比较节点哪个大,哪个小--->传入左边小右边大也可以
	LPNODE min = first->key > second->key ? second : first;     //左边
	LPNODE max = first->key > second->key ? first : second;     //右边
    //小的放左边 大的放右边
	parentNode->LChild = min;
	parentNode->RChild = max;
    //处理两个小节点的父节点--->连接
	first->parentNode = parentNode;
	second->parentNode = parentNode;
	return parentNode;
}

?遍历哈夫曼树?- - -> 递归法遍历

//打印当前节点
void printCurNode(LPNODE curNode) 
{
	printf("%d\t", curNode->key);
}
void preOrder(LPTREE root) 
{
	if (root != NULL) 
	{
		printCurNode(root);
		preOrder(root->LChild);
		preOrder(root->RChild);
	}
}

?把数组的数据插到堆中去

//要插入的堆 
void insertArrayToHeap(LPHEAP heap, int array[], int arrayNum)
{
	for (int i = 0; i < arrayNum; i++) 
	{
		insertHeap(heap, createNode(array[i])); //把整个数组的元素都插进去了,插入的是哈夫曼树的节点不是int型数据
	}
}

?创建哈夫曼树 - - -> 通过数组创建树，传入数组长度

LPTREE createhuffmanTree(int array[], int arrayNum) 
{
	if (arrayNum <= 0)               //数组长度<0返回NULL
		return NULL;
	else if (arrayNum == 1)
		return createNode(array[0]); //数组长度==1返回1个节点
	else                             //其他情况需要做树的构建
	{
		LPHEAP heap = createHeap();  //构建一个堆,需要先把数据插到堆中去,再从堆中挑两个最小的出来
		insertArrayToHeap(heap, array, arrayNum);
		LPTREE root = NULL;          //根节点
        //从堆中挑两个最小的
		while (!empty(heap))         //堆!=NULL出堆 | 从堆中挑两个最小的出来
		{
			LPNODE first = popHeap(heap);    //第一个元素出堆
			LPNODE second = popHeap(heap);   //第二个元素出堆
			root = createhuffmanNode(first, second);
			if (empty(heap))          //如果堆刚好出完了,此时堆为空就没必要丢进去
				break;
			insertHeap(heap, root);   //把新节点丢到堆中去,再拿两个最小的出来
		}
		return root;
	}
}

查找某一个关键字

哈夫曼树的父节点与子节点没有关系，不能用递归的方式去查找，通过栈，要用回退的思想去做查找

不是边走边退，是左边走到底后，才开始出栈，找到节点后退出

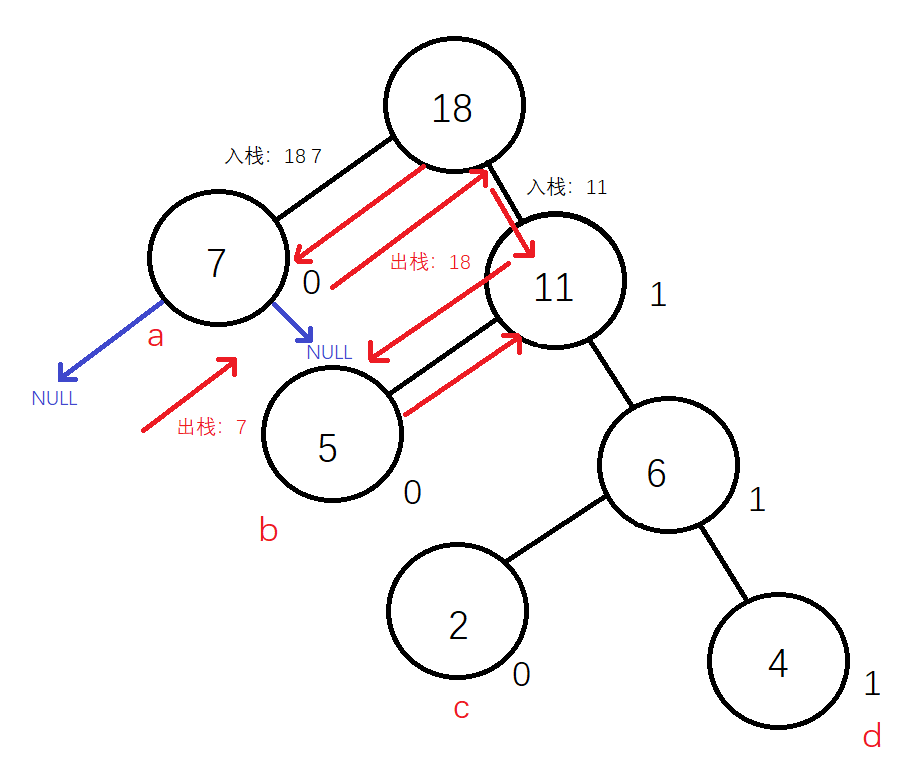
LPNODE searchhuffmanTree(LPTREE tree, int key) 
{
	LPNODE pMove = tree;
	LPNODE stack[MAX];
	int top = -1;
	while (pMove != NULL || top != -1) 
	{
		while (pMove != NULL && pMove->key != key) 
		{
			stack[++top] = pMove;    //把走过的路径入栈
			pMove = pMove->LChild;   //先走左边走到底
		}
		if (pMove == NULL)           //==NULL退出循环,走到最左边
		{
			pMove = stack[top--];    //走到最左边,出栈
			pMove = pMove->RChild;   //出栈走右边去找
		}
		else if (pMove->key == key)  //找到了退出循环
		{
			break;
		}
	}
	return pMove;
}

打印哈夫曼编码 - - -> 每个编码都属于叶子层

假设传入叶子节点? 5，让它依次往上走，走一个节点就入一次栈，走一个节点就入一次栈，[ 因为编码是从上往下走的，出栈的时候直接下来，把编码入栈后出栈即可 ] 走到 parentNode 为 NULL 的位置即可

void printCode(LPNODE leaf)
{
	LPNODE pMove = leaf;
	int stack[MAX];
	int top = -1;
	while (pMove!=NULL) 
	{
		if (pMove->parentNode != NULL && pMove->parentNode->LChild == pMove) //父节点不为空说明存在父节点,判断是父节点的左边还是右边
		{
			stack[++top] = 0;      //如果是左子树入0
		}
		else if (pMove->parentNode != NULL && pMove->parentNode->RChild == pMove) 
		{
			stack[++top] = 1;      //如果是右子树入1
		}
		else                       //为空直接break--->到达根部|只有根节点没有父节点
		{
			break;
		}
		pMove = pMove->parentNode; //依次往上走
	}
	while (top != -1) 
	{
		printf("%d", stack[top--]);//出栈打印编码
	}
	printf("\n");
}

int main() 
{
	int array[] = { 7,4,5,2 };
	LPTREE tree = createhuffmanTree(array, 4);    //创建哈夫曼树
	printf("huffmanTree:\n");
	preOrder(tree);                               //先序打印
	printf("\nhuffman code:\n");
	for (int i = 0; i < 4; i++)                   //把每个节点的编码都打印出来
	{
		printf("%d:", array[i]);                  
		printCode(searchhuffmanTree(tree, array[i]));
	}
	return 0;
}

/*输出*/
huffmanTree:                                      //带权路径长度最小的二叉树
18    7    11    5    6    2    4                 
huffman code:                                     //打印每个数字的编码
7:0
4:111
5:10
2:110