[数据结构与算法]蓝桥杯纸牌三角型

https://www.lanqiao.cn/problems/639/learning/
A,2,3,4,5,6,7,8,9 共 99 张纸牌排成一个正三角形（AA 按 11 计算）。要求每个边的和相等。 下图就是一种排法。

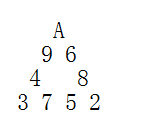
这样的排法可能会有很多。

如果考虑旋转、镜像后相同的算同一种，一共有多少种不同的排法呢？

请你计算并提交该数字。

这道题目用全排列还是可以想到的。但是问题是考虑选转镜像后相同的算一种是什么意思呢？

画图解释一下：
旋转三种图

镜像翻转三种图：

这六种情况是一样的。

注：虽然这六种情况的边长都是一样的，但是不可以把边长一样的作为相同的判定条件。

这两个三角形边长都是一样的，但是却无法镜像或者旋转得到。

那我们怎么把相同的三角形（就是那6种）排除成1种呢？

把答案 / 6即可。
可以这么想，上面6个为一组，所有答案里面有多少组那样的，即为答案。

代码：

#include <iostream>
#include <algorithm>

using namespace std;

int card[] = {1,2,3,4,5,6,7,8,9};
int ans;

bool isValid(int* card)
{
	int s1 = 0, s2 = 0, s3 = 0;
	for(int i = 0; i < 4; i++) s1 += card[i];
	for(int i = 3; i < 7; i++) s2 += card[i];
	s3 = card[6] + card[7] + card[8] + card[0];
	
	if(s1 == s2 && s2 == s3 && s1 == s3) return true;
	return false;
}

int main()
{
	do
	{
		if(isValid(card))
			ans++;
    }while(next_permutation(card, card + 9));
	
	cout << ans / 6;	
}

注：求边长的时候要注意下标的正确性。它并不是按顺序求和的。