[数据结构与算法]利用scikit中的遗传算法求解(整数01)约束规划实例详解教程+利用scipy.optimize求解约束规划问题

注意标准形式

下面两个方法约束规划的一般标准形式为：

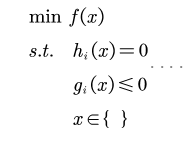
利用scikit-opt的遗传算法求解约束规划问题

先放上链接：scikit-opt网址
主要四个步骤：
下面依照此题多约束为例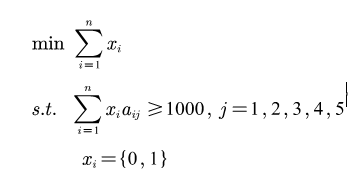

可知该题有5个不等式约束，且决策变量为01整数，后面将具体讲解如何将目标函数的约束条件加入GA模型中

一：import scikit-opt库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sko.GA import GA  ###########此行为调出scikit-opt中的遗传算法
###########
#若安装
#则： pip install scikit-opt
#####################################

二：定义目标函数

看线面的代码我们发现里面有个参数p，这个参数我理解就是GA中的某一个种群，真正调用这个函数的时候我们不需要写参数和括号

def schaffer(p):
    '''
    目标函数: min(xi)求和
    决策变量维度：n
    决策变量类型：0 1 整数
    :param p:
    :return:
    '''
    x=np.array(p)###转化为数组
    return sum(x)###返回将目标函数的值

三：定义约束

注意这里遗传算法中的约束应该默认为≤0的形式，而且不管有多少个约束，最终将约束的值及你给过一个max函数累加后返回，同样这里也需要决策变量，这里也是参数P，我们真正调用时，不需要写括号和参数

def constraint_yueshu(p):
	####注意这里的p就是种群，对应本约束问题，就是x，但是p是个一维的数据，若想利用矩阵计算，可将p reshape，即进行尺寸的转化
    x=np.array(p)###转化为一维数组
    he = 0
    for j in range(5):###由于这里面涉及到5个约束，且形式相似，因此利用for循环计算，也可单独计算，而决策变量的约束系数aij是一个二维数组
        tem=0
        for i in range(n):###这里的n就是决策变量的维度（个数）
           tem+=x[i]*a[i][j]
        ##这一层for循环结束后计算出了一个约束条件的值
        he+=max(0,tem)
    ###这一层的for循环结束后就计算出了所有的约束条件的值（不是严格意义的数值，而是大于或小于0）
    #这里的max（0，tem）是关键，因为第二层for循环结束后就是计算出了一个约束条件的值，如果该值＜0证明满足约束，max（0，tem）将返回0，对结果没有影响，若＞0则返回该值，最终的约束条件值得和->he必然＞0，即只要有一个约束不成立，那么最终返回值就是＞0得，也即这个种群对应的决策变量值不满足约束
    print(he)###这个只是便于检测约束和，看是否满足约束
    return he
constraint= [constraint_yueshu]
###注意这里的调用计算约束函数的函数并没有写括号，传参数

四：代入模板函数，设定相关参数

n=10##设定决策变量x的个数
ga = GA(func=schaffer, n_dim=n, size_pop=50, max_iter=800, prob_mut=0.001, lb=[0]*n, ub=[1]*n, precision=[1]*n，constraint_ueq=constraint)
###注意这里的目标函数schaffer并没有写括号，传参数
best_x, best_f = ga.run()
###这里的best_x就会返回最终的最优决策变量值，所有决策变量的取值
###这里的best_f就会返回最终的最优目标函数值
print('best_x:', best_x, '\n', 'best_y:', best_f)

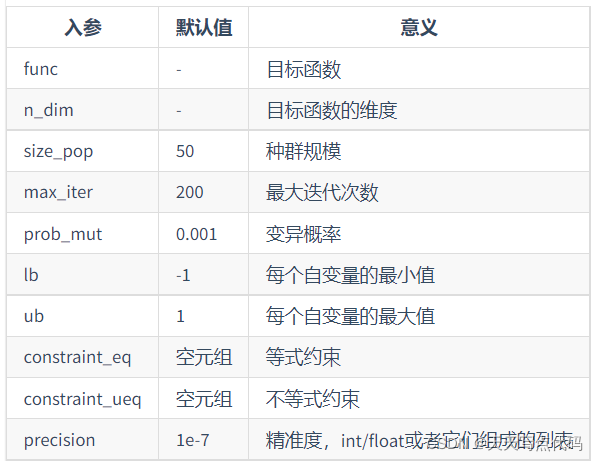
参数说明：（官方文档有）

五：结果可视化

Y_history = pd.DataFrame(ga.all_history_Y)
fig, ax = plt.subplots(2, 1)
ax[0].plot(Y_history.index, Y_history.values, '.', color='red')
Y_history.min(axis=1).cummin().plot(kind='line')
plt.show()
####这里是分别画出了每代Y_history.index中的各种群目标函数值Y_history.values和最优值Y_history.min

六：完整代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sko.GA import GA  ###########此行为调出scikit-opt中的遗传算法
###########
#若安装
#则： pip install scikit-opt
#####################################
def schaffer(p):
    '''
    目标函数: min(xi)求和
    决策变量维度：n
    决策变量类型：0 1 整数
    :param p:
    :return:
    '''
    x=np.array(p)###转化为数组
    return sum(x)###返回将目标函数的值
def constraint_yueshu(p):
	####注意这里的p就是种群，对应本约束问题，就是x，
	####但是p是个一维的数据，若想利用矩阵计算，可将p reshape，即进行尺寸的转化
    x=np.array(p)###转化为一维数组
    he = 0
    for j in range(5):
    ###由于这里面涉及到5个约束，且形式相似，因此利用for循环计算，
    ###也可单独计算，而决策变量的约束系数aij是一个二维数组
        tem=0
        for i in range(n):###这里的n就是决策变量的维度（个数）
           tem+=x[i]*a[i][j]
        ##这一层for循环结束后计算出了一个约束条件的值
        he+=max(0,tem)
    ###这一层的for循环结束后就计算出了所有的约束条件的值（不是严格意义的数值，而是大于或小于0）
    #这里的max（0，tem）是关键，因为第二层for循环结束后就是计算出了一个约束条件的值，
    #如果该值＜0证明满足约束，max（0，tem）将返回0，对结果没有影响，
    #若＞0则返回该值，最终的约束条件值得和->he必然＞0，
    #即只要有一个约束不成立，那么最终返回值就是＞0得，也即这个种群对应的决策变量值不满足约束
    print(he)###这个只是便于检测约束和，看是否满足约束
    return he
constraint= [constraint_yueshu]##这一块是真正代入模板的
n=10##设定决策变量x的个数
ga = GA(func=schaffer, n_dim=n, size_pop=50, max_iter=800, prob_mut=0.001, lb=[0]*n, ub=[1]*n, precision=[1]*n，constraint_ueq=constraint)
###注意这里的目标函数schaffer并没有写括号，传参数
best_x, best_f = ga.run()
###这里的best_x就会返回最终的最优决策变量值，所有决策变量的取值
###这里的best_f就会返回最终的最优目标函数值
print('best_x:', best_x, '\n', 'best_y:', best_f)
Y_history = pd.DataFrame(ga.all_history_Y)
fig, ax = plt.subplots(2, 1)
ax[0].plot(Y_history.index, Y_history.values, '.', color='red')
Y_history.min(axis=1).cummin().plot(kind='line')
plt.show()


###注意这里并没有给出二维矩阵a的值，只是举例子

利用scipy.optimize求解

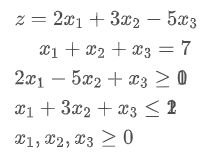
详细见代码
参考自：代码来源

'''参考自：https://blog.csdn.net/qq_39241986/article/details/104832513'''
import numpy as np
from scipy.optimize import minimize
###定义目标函数
def objective(x):
    return x[0]**2+x[1]**2+x[2]**2+8
###定义约束条件
def constraint1(x):#不等约束
    return x[0]**2-x[1]+x[2]**2
def constraint2(x):#不等约束
    return -(x[0]+x[1]**2+x[2]**2-20)
def constraint3(x):#等式约束
    return -x[0]-x[1]**2+2
def constraint4(x):#等式约束
    return x[1]+2*x[2]**2-3
con1 = {'type': 'ineq', 'fun': constraint1}
con2 = {'type': 'ineq', 'fun': constraint2}
con3 = {'type': 'eq', 'fun': constraint3}
con4 = {'type': 'eq', 'fun': constraint4}
###四个约束条件
cons=([con1,con2,con3,con4])
##此处的多约束也可仿照上面GA算法中的思想计算约束值之和，最终相当于只输出一个约束
##而等式约束可以考虑为tem+=man(0,绝对值)

##决策变量的符号约束
b=(0,None)
bnds=(b,b,b)

###求解
x=np.array([0,0,0])#定义初始值
solution=minimize(objective,x,method='SLSQP',bounds=bnds,constraints=cons)

##打印结果
x=solution.x
print('目标值: ' + str(objective(x)))
print('最优解为')
print('x1 = ' + str(round(x[0],2)))
print('x2 = ' + str(round(x[1],2)))
print('x3 = ' + str(round(x[2],2)))
print(solution)

利用geatpy

注意，其实仔细看geatpy官方文档是比较好改的。需要改的也只有自定义的目标函数了，虽然看着后面很多代码很复杂，但是其实都不用动。
可以看官方文档中的《数据结构》和《快速入门》来改函数。
看数据结构方便自己自定义目标函数的约束条件。
文档网址

import numpy
import pip

import pandas as pd
import numpy as np
import geatpy as ea
#########################
weidu=402
#########################
#############读取数据
path='E:\桌面\gyx.xlsx'
dataframe=pd.read_excel(path,'供')
data=dataframe.iloc[0:402,1:dataframe.shape[1]].values
########################################################################
class MyProblem(ea.Problem): # 继承Problem父类
    def __init__(self):
        name = 'MyProblem' # 初始化name（函数名称，可以随意设置）
        M = 1 # 初始化M（目标维数）
        maxormins = [1] # 初始化目标最小最大化标记列表，1：min；-1：max
        Dim = weidu # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim # 初始化决策变量类型，0：连续；1：离散
        #这是一个list,初始化varTypes(决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的)
        lb = [0]*Dim # 决策变量下界
        ub = [1]*Dim # 决策变量上界
        lbin = [1]*Dim # 决策变量下边界(0表示不包含该变量的下边界，1表示包含)
        ubin = [1]*Dim # 决策变量上边界(0表示不包含该变量的下边界，1表示包含)
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb,ub, lbin, ubin)
    def aimFunc(self, pop): # 目标函数，pop为传入的种群对象
        Vars = pop.Phen  # 得到决策变量矩阵,行表示一完整个体，列表示一个决策变量（参见geatpy数据结构文档）
############################################################################################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        # x1 = Vars[:, [0]]  # 取出第一列得到所有个体的x1组成的列向量
        # x2 = Vars[:, [1]]  # 取出第二列得到所有个体的x2组成的列向量
        # x3 = Vars[:, [2]]  # 取出第三列得到所有个体的x3组成的列向量
#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处
        #取出第i列得到所有个体的x[i]组成的列向量
        #######################################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        x=[[] for i in range(weidu)]
        for i in range(weidu):
            x[i]=Vars[:,[i]]
        ##############
###########################################################################################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        #计算目标函数值，赋值给pop种群对象的ObjV属性
        # pop.ObjV = 4 * x1 + 2 * x2 + x3
        # print('Pop.objv:',pop.Objv)
        # # 采用可行性法则处理约束，生成种群个体违反约束程度矩阵
        # pop.CV = np.hstack([2 * x1 + x2 - 1,  # 第一个约束
        #                     x1 + 2 * x3 - 2,  # 第二个约束
        #                     np.abs(x1 + x2 + x3 - 1)])  # 第三个约束
#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处#改动之处
        #######################################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        ##############改动之处##################
        # # 计算目标函数值，赋值给pop种群对象的ObjV属性
        ##如何改动可参看geatpy数据结构ObjV这样就知道了
        pop.ObjV=x[0]
        for i in range(1,weidu):
            pop.ObjV +=x[i]
        # 采用可行性法则处理约束，生成种群个体违反约束程度矩阵
        list = []
        for i in range(24):
            tem = 0
            for j in range(weidu):
                if data[j][0] == 'A':
                    tem += data[j][i + 1] * x[j] / 0.6
                elif data[j][0] == 'B':
                    tem += data[j][i + 1] * x[j] / 0.66
                else:
                    tem += data[j][i + 1] * x[j] / 0.72
            list.append(2*1e4-tem)
        pop.CV = np.hstack(list)


###########################################################################################
"""============================实例化问题对象========================"""
problem = MyProblem() # 实例化问题对象
"""==============================种群设置==========================="""
Encoding = 'RI' # 编码方式
NIND = 100 # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,
problem.borders) # 创建区域描述器
population = ea.Population(Encoding, Field, NIND) #
#实例化种群对象（此时种群还没被真正初始化，仅仅是生成一个种群对象）
"""===========================算法参数设置=========================="""
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population) #

#实例化一个算法模板对象
myAlgorithm.MAXGEN = 1500 # 最大进化代数
myAlgorithm.mutOper.F = 0.6 # 差分进化中的参数F
myAlgorithm.recOper.XOVR = 0.8 # 设置交叉概率
myAlgorithm.logTras = 100 #
#设置每隔多少代记录日志，若设置成0则表示不记录日志
myAlgorithm.verbose = True # 设置是否打印输出日志信息
myAlgorithm.drawing = 1 #
#设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
"""==========================调用算法模板进行种群进化==============="""
[BestIndi, population] = myAlgorithm.run() #
#执行算法模板，得到最优个体以及最后一代种群
BestIndi.save() # 把最优个体的信息保存到文件中
"""=================================输出结果======================="""
print('评价次数：%s' % myAlgorithm.evalsNum)
print('时间已过 %s 秒' % myAlgorithm.passTime)
if BestIndi.sizes != 0:
    print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
    print('最优的控制变量值为：')
    for i in range(BestIndi.Phen.shape[1]):
        print(BestIndi.Phen[0, i])
else:
    print('没找到可行解。')

注：此题的例子是2021数学建模国赛的C题066论文约束规划问题的简化