[数据结构与算法]2018蓝桥杯省赛 真题 小朋友崇拜圈（DFS）

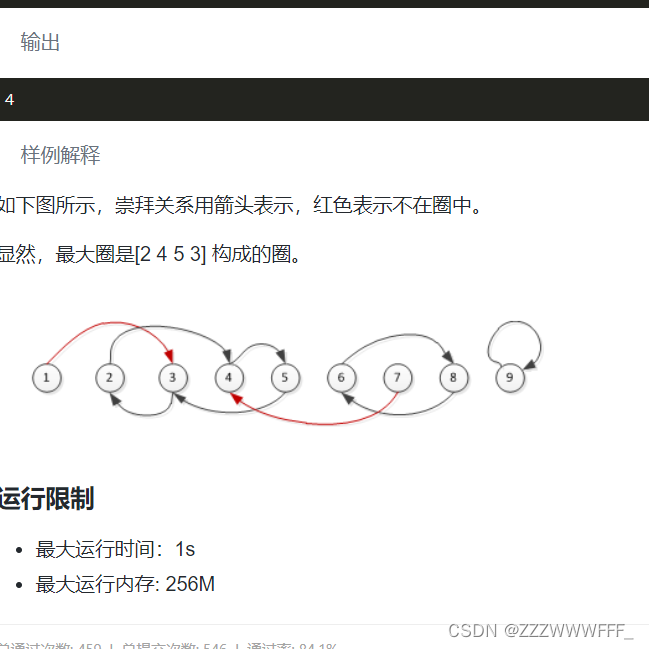
看到该题的第一反应就是要使用DFS了，该题很明显地出现了DFS的特点——一条路走到底才回头

不过我还是没有完全掌握DFS，写出来的代码还结合了一点暴力（不过还好AC了）?

我的思路是用DFS去搜索每一个没有走过的路（或者说崇拜对象），直到某一个人的崇拜对象我已经走过的时候，我们就return，在搜索的过程中我们同时将每个人的崇拜对象输入一个vector中，然后搜索结束的时候我们就遍历这个vector（即我说的暴力，用了嵌套for循环），目的是找到这个vector中两个相同的崇拜对象的下标，然后我们发现这两个下标相减刚好就是他们形成的圈的人数，之后循环上面的这个过程，且比较前后的圈的大小，最后输出最大圈人数即可

值得注意的是我们每次dfs之前都要记得clear那个vector，还有对于已经走过的地方（崇拜对象），我们也不必再走，还有index1与index2记得每次搜索前都要初始化，不然可能出现数组越界情况（最好自己调试）

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include <iomanip>
#include<cmath>
using namespace std;
vector<int> v;
const int MAX = 100005;
int per[MAX];
int book[MAX] = { 0 };
int cn = 0;
void dfs(int per[], int book[], int x, int n)
{
	if (book[x] == 1)
	{
		v.push_back(x);
		return ;
	}

	book[x] = 1;
	v.push_back(x);
	dfs(per, book, per[x], n);
	return ;
}

int main()
{
	int n, max_per = 0, index1=0, index2=1,i,j,z;
	cin >> n;
	for ( i = 1; i <= n; i++)
	{
		cin >> per[i];
	}
	for ( i = 1; i <= n; i++)
	{
		v.clear();
		if (!book[i])
		{
			index1 = 0;
			index2 = 1;
			dfs(per, book, i, n);
			for ( z = 0; z < v.size(); z++)
			{
				for ( j = 0; j < v.size(); j++)
				{
					if (z == j)
					{
						continue;
					}
					if (v[z] == v[j])
					{
						index1 = z;
						index2 = j;
						break;
					}
				}
				if (v[index1] == v[index2])
				{
					break;
				}
			}
			max_per = max(max_per, (index2 - index1));
		}
	}

	cout << max_per << endl;
	return 0;
}

总的来说自己写的这个DFS还是太冗长了（不够精炼），还是要多做题~~~?

下面是原题给出的题解（很简洁）

该思路：我们发现我们得到的数据肯定都至少会形成一个“崇拜圈”，而且必然会有“从哪里来回哪里去”的情况，那么不妨我们就一个一个试，遍历每一个孩子作为崇拜圈的起点，如果可以回到起点，我们就记录下来并且在后面找到新的崇拜圈的时候更新最大值（记得每次dfs之前需要将visited重新初始化）

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include <iomanip>
#include<cmath>
using namespace std;
int a[100005];
int n, ans = 0;
int vt[100005];
void dfs(int x, int y, int t) {
	if (x == y) {//回到起点
		ans = max(ans, t);
		return;
	}
	if (!vt[x]) {
		vt[x] = 1;
		dfs(a[x], y, t + 1);
	}
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++) {
		memset(vt, 0, sizeof(vt));
		vt[i] = 1;
		dfs(a[i], i, 1);
	}
	cout << ans << endl;
	return 0;
}