[数据结构与算法]leetcode70.爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：
输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：
输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
3. 1 阶 + 1 阶 + 1 阶
4. 1 阶 + 2 阶
5. 2 阶 + 1 阶

思路：

题目很明显是一个递归问题，可以将整体问题划分为多个小问题：

我们先假设楼梯只有一阶，也就是 n 为1；此时只有一种办法能爬到楼梯，也就是一次爬一阶楼梯。
我们再假设楼梯只有二阶，也就是 n 为2；此时有两种办法能爬到楼梯，一种是一次爬两阶楼梯，一种是爬两次一阶楼梯。

我们再来看楼梯只有三阶，也就是 n 为3；此时问题可以划分为多个子问题，也就是 第一步爬一阶楼梯的所有情（可以表示成 楼梯还剩下n-1的所有走法）加上 第一步爬二阶楼梯（可以表示成楼梯还剩下n-2 的所有走法）的所有情况。

如果用函数来表示以上文字的话。

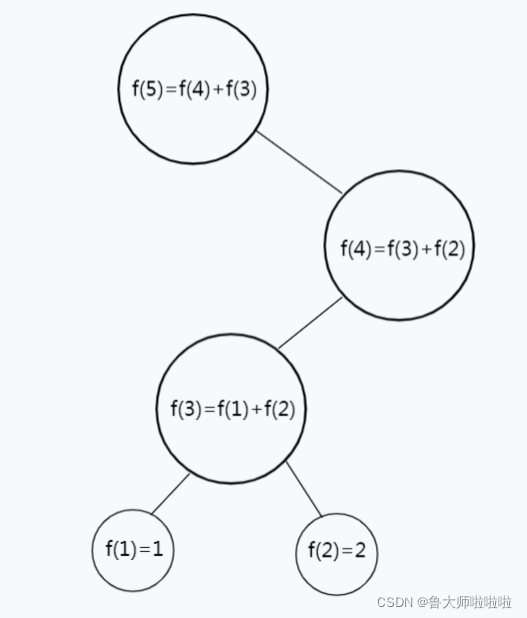
代码如下：

class Solution {
    public int climbStairs(int n) {
        if(n==1){
            return 1;
        }       
        if(n==2){
            return 2;
        }
        return climbStairs(n-1)+climbStairs(n-2);
    }
}

我们提交以上代码发现出现超出时间限制的问题，原因是使用以上递归，虽然代码简单，但是进行了多次的重复计算。

进一步改进，使用 HashMap 来保存我们已经求解过的值。首先从 HashMap 中判断当前 f(n) 是否已经计算过，如果计算过，直接取出数据返回。如果 HashMap 中没有当前 f(n) 的值则将计算的值保存到 HashMap 中。

class Solution {
    private HashMap<Integer,Integer> storeMap = new HashMap<>();
    public int climbStairs(int n) {
        if(n == 1){
            return 1;
        }
        if(n == 2){
            return 2;
        }
        if(storeMap.get(n) != null){
            return storeMap.get(n);
        }else{
            int result = climbStairs(n-1) + climbStairs(n-2);
            storeMap.put(n,result);
            return result;
        }
    }
}