[数据结构与算法]【LeetCode - Java】50. Pow(x n)（中等）

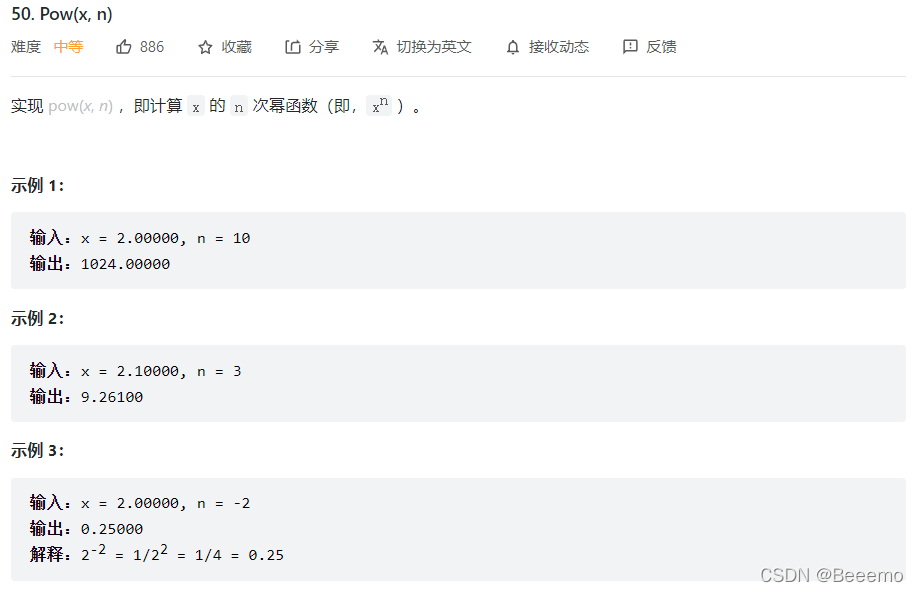
1. 题目描述

2. 解题思路

上一次看见这种类型的题目还是在上一次…例如这个【LeetCode - Java】69. Sqrt(x) （简单），或者更离谱的这个【LeetCode - Java】29. 两数相除（中等）| 地狱难度。于是乎在这里我先尝试了使用牛顿迭代法去逼近，发现这道题若使用牛顿迭代法的目标答案只能转化为 $log(ans)$ ，显然答案就不能为负数了，因此牛顿迭代法无法解决这一道题目，然后我就转向了位运算的思路。

在“两数相除”那道题目中，是把除数不断地分次向左位移实现模拟乘二的效果，最后相加得出商，其实是属于一种分治的思想。下面我们来观察一下幂函数计算可以分解为什么，对于$5^3$，它可以分解为$5^2?5^1$，那么对于$5^{31}$呢？它可以分解为$5^{16}+5^8+5^4+5^2+5^1$。这时候你会有疑问了，分解开有什么用， 它可以加快幂运算吗？ 下面我们来捋一捋。

假如我们计算$5^{31}$，我们需要算30次乘法；但如果计算$5^{16}?5^8?5^4?5^2?5^1$呢？发现规律了吗？$5^{16}$刚好是$5^8$的平方，而$5^8$也刚好是$5^4$的平方，换言之我们只需要进行4次乘法即可得出答案了，显然这可以大大提高效率。

其实分解公式是简化了的，对于$5^{31}$，31的二进制表示是11111，因此分解成

• $5^{2^4}?5^{2^3}?5^{2^2}?5^{2^1}?5^{2^0}=5^{16}?5^8?5^4?5^2?5^1$

而如果对于$5^{10}$，10的二进制表示是1010，那么就应该分解成

• $5^{2^3}?5^0?5^{2^1}?5^0=5^8?5^2$

显然，如何累乘是与指数的二进制表示有关，因此在实际编程中可以先求出指数的二进制表示，再进行答案构建，也可以把指数的二进制生成与答案生成同时进行，以节省时间与空间。

另外，提醒一个有意思的点，在int中把Integer.MIN_VALUE转换为相反数会溢出我相信大家都是能够理解的，但是很神奇的是在代码中进行n=-n的操作后居然是原样不变的，即对-2147483648取负的答案依然是-2147483648。我猜应该大家都猜到了这是由于原码反码补码的关系，详细我就不在这里叙述了，有兴趣可以推导一下，这也是这里代码实现中所需要注意的一个小细节。

3. 代码实现

3.1 快速幂 先求指数二进制

public double myPow(double x, int n) {
        if (n == 0 || x == 1)
            return 1;
        if (n < 0) {
            x = 1 / x;
            n = -n;
        }
        StringBuilder sb = new StringBuilder();
        while (n != 0) {
            sb.append(n % 2);
            n /= 2;
        }
        char[] chars = sb.toString().toCharArray();
        System.out.println(sb);
        double ans = 1;
        double temp = x;
        if (chars[0] == '1')
            ans = x;
        for (int i = 1; i < chars.length; i++) {
            temp *= temp;
            if (chars[i] == '1') {
                System.out.println(i);
                ans *= temp;
            }
        }
        return ans;
    }

3.2 快速幂 同时求指数二进制

public double myPow(double x, int n) {
        if (n == 0 || x == 1)
            return 1;
        if (n < 0) {
            x = 1 / x;
            n = -n;
        }
        double ans = 1,temp = x;
        while (n != 0) {
            if (n % 2 == 1||n % 2 == -1){
                ans *= temp;
            }
            temp *= temp;
            n /= 2;
        }
        return ans;
    }

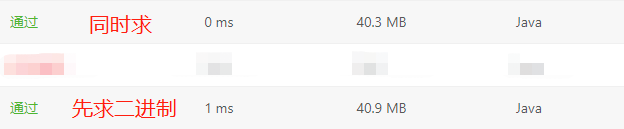
3.3 对比

先求二进制表示的解法一共循环了2logn次，而同时求的解法一共循环了logn次，因此两种解法的时间复杂度都是O(logn)，实际表现上同时求更优；而同样的，先求二进制表示的解法需要额外的空间存储二进制表示字符串，因此其空间复杂度是O(logn)，而同时求不需要，空间复杂度为O(1)。