差分数组:PIPI的区间操作Ⅰ
差分数组
??差分数组其实就是对数组做差分,即前一项减去后一项,差分数组的定义为:对于有n个元素的数组a,差分数组b为数组a中每一项与前一项的差值。显然,b[1]=a[1]-0=a[1];对于整数i∈[2,n],则有b[i]=a[i]-a[i-1]。例子如下:
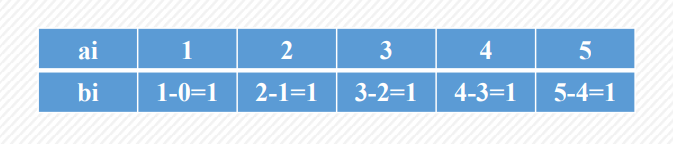
??我们不难发现,设sum数组为b数组的前缀和数组,那么sum数组的值和a数组的值是对应相等的,也就是说,相对于数组a的差分数组b来说,a数组就是其前缀和数组。这是差分数组的重要性质,差分数组的前缀和对应原数组,也就是我们可以将差分数组通过前缀和还原为原数组
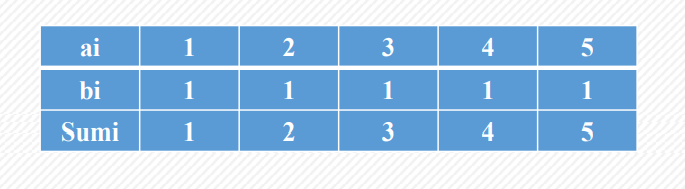
??那么差分数组有什么作用呢?答案是快速处理区间加减操作。例如对区间[L,R]中的每个数加上x,我们通过差分数组的性质知道,第一个受影响的差分数组中的元素为b[L],因为a[L]加上了x,a[L - 1]没有加,所以令b[L]+=x;最后一个受影响的差分数组中的元素为b[R+1],因为a[R]加上了x,a[R + 1]没有加,所以令b[R+1]-=x。

??这样对于区间加减操作,我们不必对区间内每一个数进行处理,只需处理两个差分后的数即可。例如,我们要对a数组[2,3]区间的每个数加上3,再对a数组[3,4]区间的每个数加上1,求最终a数组的每个数是多少:
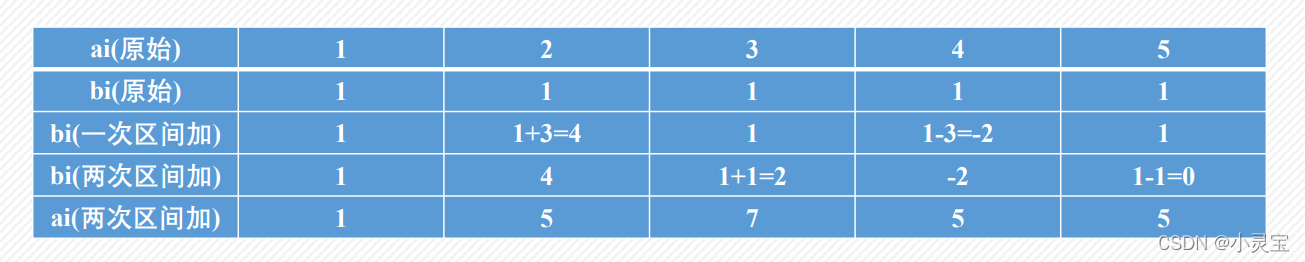
??差分数组特别适合解决多次区间加减操作,最后再询问的问题。例如,若需要对区间进行n次加减,最后求区间和,用for循环的时间复杂度为O(n ^ 2),而使用差分数组的时间复杂度为O(n)。
问题:
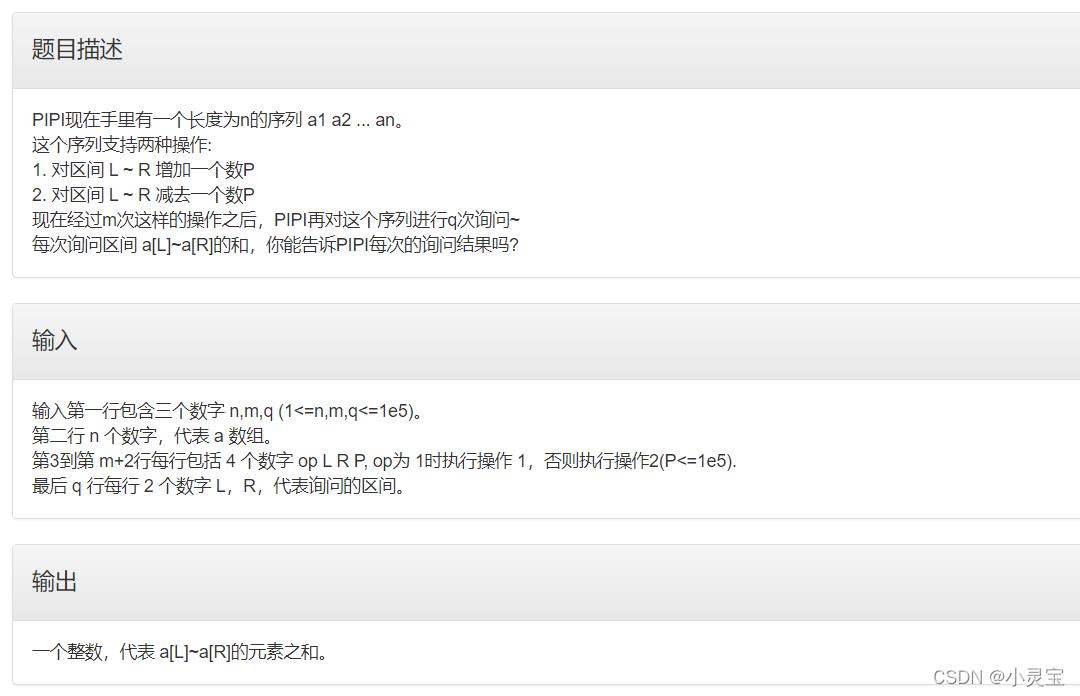
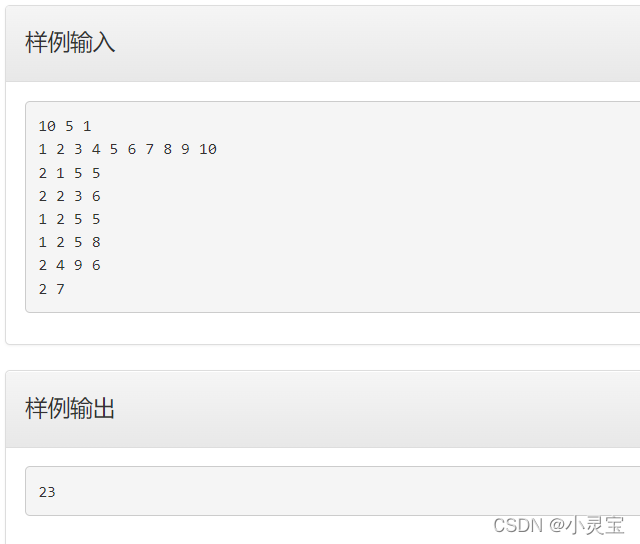
思路:
??差分数组板子题。我们对原数组a求差分数组b,那么对每个区间加操作,我们就令b[L]+=P并令b[R+1]-=P。如果是区间减操作,就令b[L]+=-P并令b[R+1]-=-P就行了。进行完m次操作后,我们对b数组求其前缀和数组,即可把它还原成经过m次操作后的a数组。然后再对a数组求前缀和sum数组,那么对接下来的q次询问,我们对每个问题输出sum[r]-sum[l-1]即可。
代码:
import java.util.*;
public class Main {
static long[] subArray = new long[100005];
static long[] array = new long[100005];
static long[] preSum = new long[100005];
public static void main(String[] args) {
int n, m, q, op, l, r, i;
long p;
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
q = scanner.nextInt();
for (i = 0; i < n; i++) {
array[i] = scanner.nextLong();
}
subArray[0] = array[0];
for (i = 1; i < n; i++) {
subArray[i] = array[i] - array[i - 1];
}
for (i = 0; i < m; i++) {
op = scanner.nextInt();
l = scanner.nextInt() - 1;
r = scanner.nextInt() - 1;
p = scanner.nextLong();
if (op == 1) {
subArray[l] += p;
if (r + 1 < n) {
subArray[r + 1] -= p;
}
} else {
subArray[l] -= p;
if (r + 1 < n) {
subArray[r + 1] += p;
}
}
}
array[0] = subArray[0];
for (i = 1; i < n; i++) {
array[i] = array[i - 1] + subArray[i];
}
preSum[0] = array[0];
for (i = 1; i < n; i++) {
preSum[i] = preSum[i - 1] + array[i];
}
for (i = 0; i < q; i++) {
l = scanner.nextInt() - 1;
r = scanner.nextInt() - 1;
System.out.println(l == 0 ? preSum[r] : preSum[r] - preSum[l - 1]);
}
}
}