引入
??MUSIC算法能有效运行的前提是矩阵 R S R_S RS?是非奇异的,即各条传播路径不相干。如果L路到达信号中存在Q路相干信号(Q≤L),则通过MUSIC算法能被检测到的信号数量为L-Q+1,能被解出的信号数量为L-Q。
??信号 s ( t ) s(t) s(t) 的协方差矩阵 R S R_S RS?的非奇异性是 MUSIC 算法有效运行 的关键。为了在存在相干信号的情况下保证 R S R_S RS?的非奇异性, 解决 MUSIC 算法失效的问题,需要使用空间平滑算法。
空间平滑算法
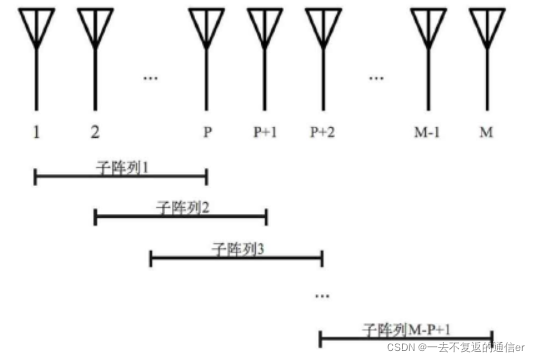
??如图所示, 首先, 将由
M
M
M 根接收天线构成的线性天线阵列划分为多个相互重叠的子阵列, 假设每个子阵列中包含的天线数量为
P
P
P, 则子阵列的数量为
M
?
P
+
1
M-P+1
M?P+1, 其中第一个子阵列包含的天线子集为
{
1
,
2
,
…
,
P
}
\{1,2, \ldots, P\}
{1,2,…,P}, 第二个子阵列包含的天 线子集为
{
2
,
3
,
…
,
P
+
1
}
\{2,3, \ldots, P+1\}
{2,3,…,P+1} 等, 直到第
M
?
P
+
1
M-P+1
M?P+1 个子阵列包含的天线子集为
{
M
?
P
,
M
?
\{M-P, M-
{M?P,M?
P
+
1
,
…
,
M
}
°
P+1, \ldots, M\}_{\circ}
P+1,…,M}°?
??第
p
p
p 个子阵列的接收信号向量
r
p
(
t
)
r_{p}(t)
rp?(t) :
r
p
(
t
)
=
A
p
s
(
t
)
+
N
p
(
t
)
r_{p}(t)=A_{p} s(t)+N_{p}(t)
rp?(t)=Ap?s(t)+Np?(t)
??其中
A
p
A_{p}
Ap? 是第
p
p
p 个阵列的方向矩阵,
N
p
(
t
)
N_{p}(t)
Np?(t) 是第
p
p
p 个子阵列的噪声向量,
s
(
t
)
s(t)
s(t) 为
L
L
L 路信号。为了体现子阵列之间的关系, 推导出空间平滑算法, 构建对角线矩阵
D
D
D :
D
=
diag
?
{
e
?
j
2
π
f
0
d
?
sin
?
θ
1
/
c
,
e
?
j
2
π
f
0
d
?
sin
?
θ
2
/
c
,
…
,
e
?
j
2
π
f
0
d
?
sin
?
θ
L
/
c
}
D=\operatorname{diag}\left\{e^{-j 2 \pi f_{0} d \cdot \sin \theta_{1} / c}, e^{-j 2 \pi f_{0} d \cdot \sin \theta_{2} / c}, \ldots, e^{-j 2 \pi f_{0} d \cdot \sin \theta_{L} / c}\right\}
D=diag{e?j2πf0?d?sinθ1?/c,e?j2πf0?d?sinθ2?/c,…,e?j2πf0?d?sinθL?/c}
则
A
p
=
A
1
D
(
p
?
1
)
A_{p}=A_{1} D^{(p-1)}
Ap?=A1?D(p?1), 其中
A
1
A_{1}
A1? 为第一个子阵列的方向矩阵,
D
(
p
?
1
)
?为:?
D^{(p-1) \text { 为: }}
D(p?1)?为:?
D
(
p
?
1
)
=
diag
?
{
e
?
j
2
π
f
0
(
p
?
1
)
d
?
sin
?
θ
1
/
c
,
e
?
j
2
π
f
0
(
p
?
1
)
d
?
sin
?
θ
2
/
c
,
…
,
e
?
j
2
π
f
0
(
p
?
1
)
d
?
sin
?
θ
L
/
c
}
D^{(p-1)}=\operatorname{diag}\left\{e^{-j 2 \pi f_{0}(p-1) d \cdot \sin \theta_{1} / c}, e^{-j 2 \pi f_{0}(p-1) d \cdot \sin \theta_{2} / c}, \ldots, e^{-j 2 \pi f_{0}(p-1) d \cdot \sin \theta_{L} / c}\right\}
D(p?1)=diag{e?j2πf0?(p?1)d?sinθ1?/c,e?j2πf0?(p?1)d?sinθ2?/c,…,e?j2πf0?(p?1)d?sinθL?/c}
??此时
r
p
(
t
)
r_{p}(t)
rp?(t) 可以改写为:
r
p
(
t
)
=
A
1
D
(
p
?
1
)
s
(
t
)
+
N
p
(
t
)
(
1
)
r_{p}(t)=A_{1} D^{(p-1)} s(t)+N_{p}(t) \qquad (1)
rp?(t)=A1?D(p?1)s(t)+Np?(t)(1)
??从(1)式可以看出, 每一个子阵列的接收信号向量均可写成同一方向矩阵的线性组合。第
p
p
p 个子阵列的接收信号
r
p
(
t
)
r_{p}(t)
rp?(t) 的协方差矩阵可以推导出来:
R
p
=
A
1
D
(
p
?
1
)
S
D
H
(
p
?
1
)
A
1
H
+
σ
2
I
(
2
)
R_{p}=A_{1} D^{(p-1)} S D^{H(p-1)} A_{1}^{H}+\sigma^{2} I \qquad (2)
Rp?=A1?D(p?1)SDH(p?1)A1H?+σ2I(2)
??其中
D
H
(
p
?
1
)
D^{H^{(p-1)}}
DH(p?1) 和
A
1
H
A_{1}^{H}
A1H? 分别为
D
(
p
?
1
)
D^{(p-1)}
D(p?1) 和
A
1
A_{1}
A1? 的共轭转置矩阵。
??计算出每个子阵列的协方差矩阵后, 定义空间平滑协方差矩阵
R
ˉ
\bar{R}
Rˉ 为所有子阵列协方差矩阵的平均值:
R
ˉ
=
1
M
?
P
+
1
∑
p
=
1
M
?
P
+
1
R
p
(
3
)
\bar{R}=\frac{1}{M-P+1} \sum_{p=1}^{M-P+1} R_{p} \qquad (3)
Rˉ=M?P+11?p=1∑M?P+1?Rp?(3)
??将公式(2)带入公式 (3) 后可得:
R
ˉ
=
A
1
(
1
M
?
P
+
1
∑
p
=
1
M
?
P
+
1
D
(
p
?
1
)
S
D
H
(
p
?
1
)
)
A
1
H
+
σ
2
I
=
A
1
S
ˉ
A
1
H
+
σ
2
I
\bar{R}=A_{1}\left(\frac{1}{M-P+1} \sum_{p=1}^{M-P+1} D^{(p-1)} S D^{H(p-1)}\right) A_{1}^{H}+\sigma^{2} I=A_{1} \bar{S} A_{1}^{H}+\sigma^{2} I
Rˉ=A1?(M?P+11?p=1∑M?P+1?D(p?1)SDH(p?1))A1H?+σ2I=A1?SˉA1H?+σ2I
??其中:
S
ˉ
=
1
M
?
P
+
1
∑
p
=
1
M
?
P
+
1
D
(
p
?
1
)
S
D
H
(
p
?
1
)
\bar{S}=\frac{1}{M-P+1} \sum_{p=1}^{M-P+1} D^{(p-1)} S D^{H(p-1)}
Sˉ=M?P+11?p=1∑M?P+1?D(p?1)SDH(p?1)
??只要能证明 S ˉ \bar{S} Sˉ是非奇异的,便可以在存在相干信号的情况下,使用MUSIC算法。
??经推导,在存在相干信号的情况下,只要保证两个条件:
????①子阵列天线数量大于信号数量 ,
M
?
P
+
1
>
L
M-P+1>L
M?P+1>L
????②子阵列数量大于信号数量这两个条件,
P
>
L
P>L
P>L
??便能使用MUSIC算法有效地探测各路信号并求解各路信号AoA。综上,线性天线阵列需要的最少天线数量为 M = 2 L M=2L M=2L,即阵列天线数量至少要为传播路径数量的两倍,相比于传统MUSIC算法的情况,牺牲了一半的有效天线孔径。
??在室内环境下,多径是源信号经过障碍物折射、反射、散射产生的,理论上各条传播路径上的信号均是源信号的副本,它们拥有相同的频率和固定的相位差,因此室内静态多径信号都是相干的。
参考文献
[1] 陈浩翔. 基于Wi-Fi信道状态信息的室内定位算法研究[D].华南理工大学,2019.
更新ing……