[数据结构与算法]第六章 二叉树（Binary Tree）

第六章 二叉树（Binary Tree）

树形结构

生活中的树形结构

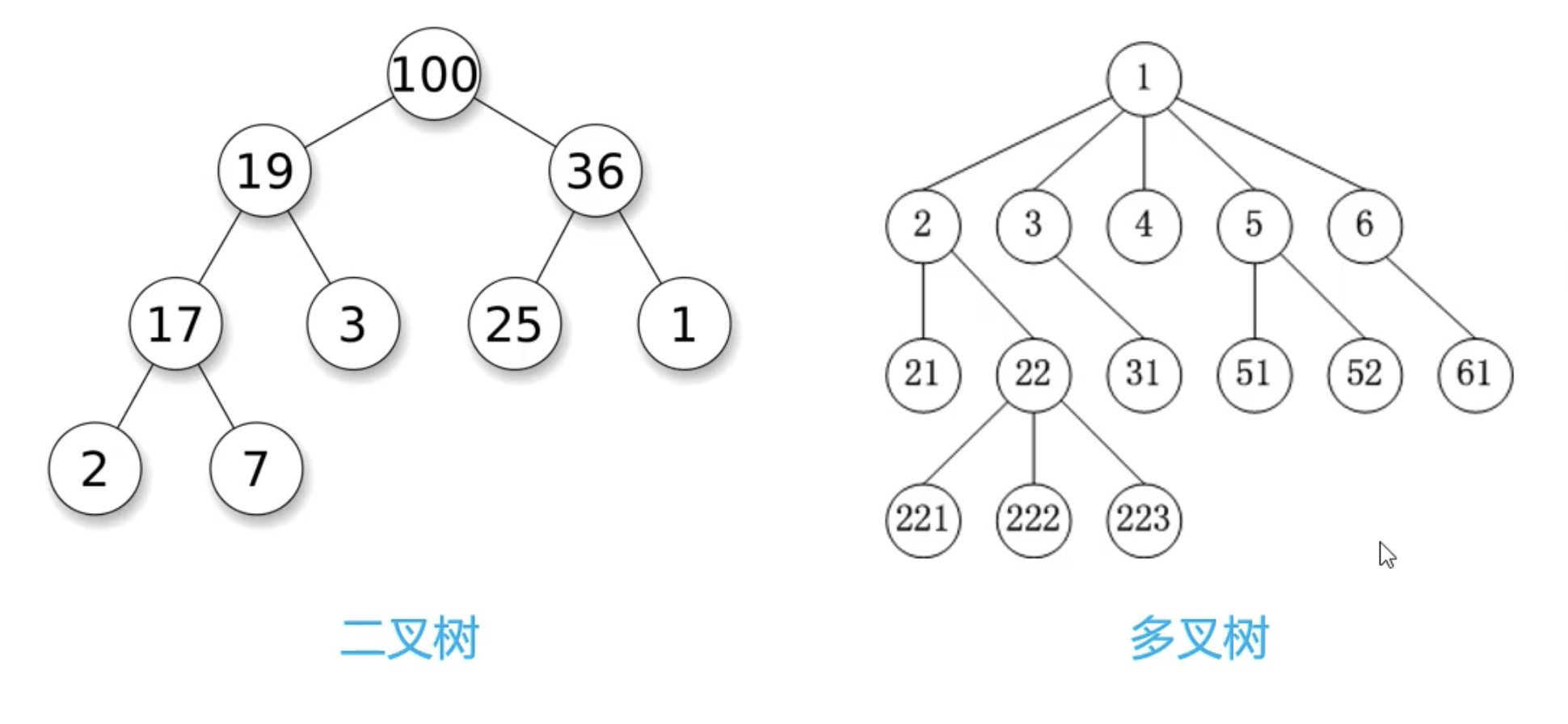
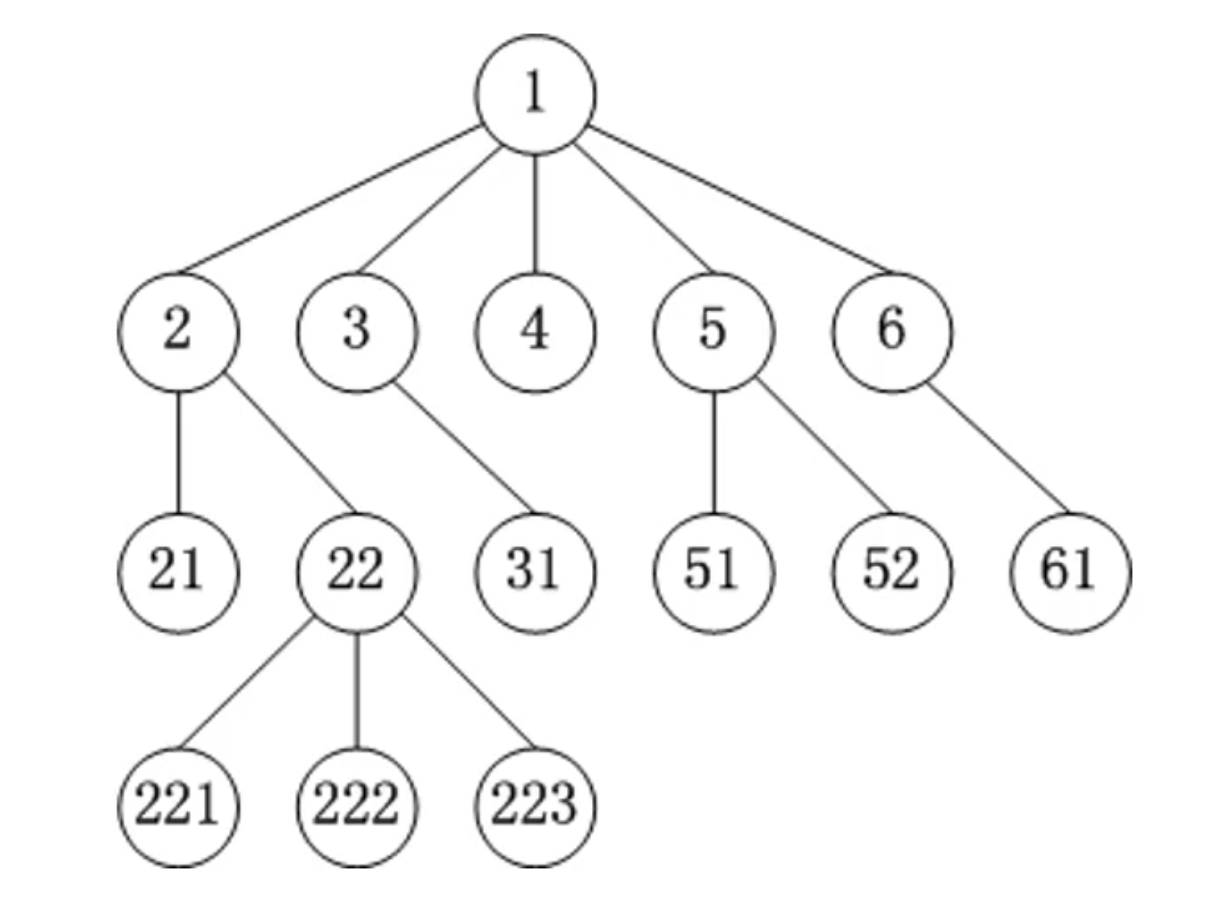
• 使用树形结构可以大大提高效率
• 树形结构是算法面试的重点

树（Tree）的基本概念

节点、根节点、父节点、子节点、兄弟节点

一棵树可以没有任何节点，称为空树

一棵树可以只有 1 个节点，也就是只有根节点

子树、左子树、右子树

节点的度（degree）：子树的个数

树的度：所有节点度中的最大值

叶子节点（leaf）：度为 0 的节点

非叶子节点：度不为 0 的节点

层数（level）：根节点在第 1 层，根节点的子节点在第 2 层，以此类推（有些教程也从第 0 层开始计算）

节点的深度（depth）：从根节点到当前节点的唯一路径上的节点总数

节点的高度（height）：从当前节点到最远叶子节点的路径上的节点总数

树的深度：所有节点深度中的最大值

树的高度：所有节点高度中的最大值

数的深度 等于 树的高度

有序树、无序树、森林

有序树：树中任意节点的子节点之间有顺序关系

无序树：树中任意节点的子节点之间没有顺序关系，也称为 “自由树”

森林：由 m（m ≥ 0）棵互不相交的树组成的集合

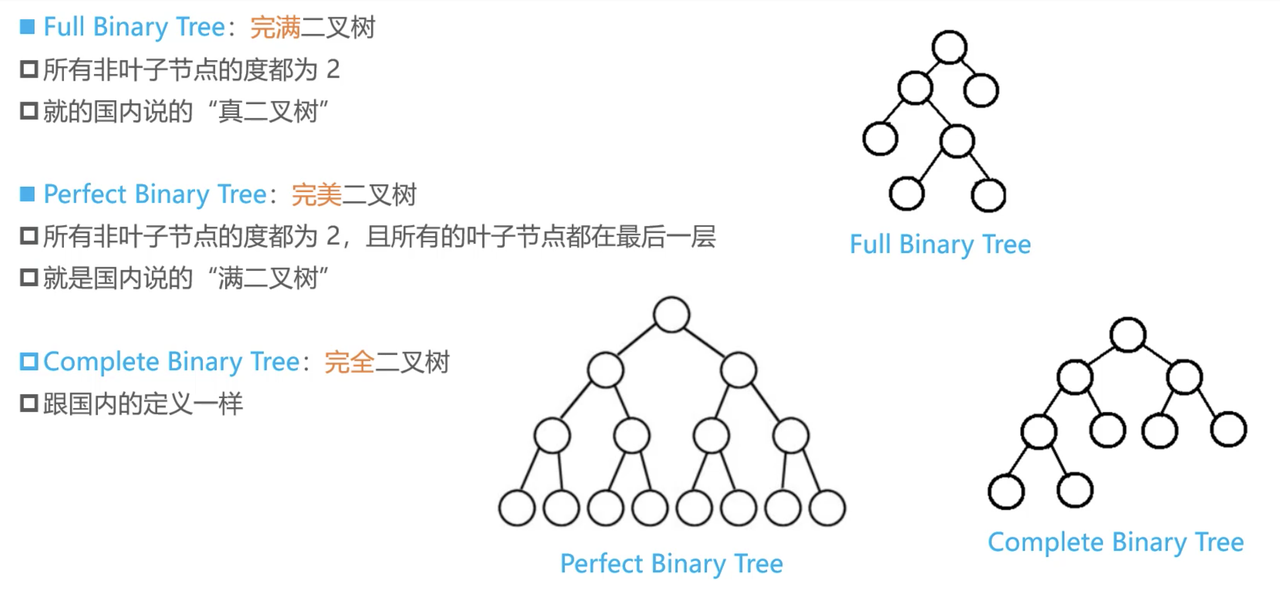
二叉树（Binary Tree）

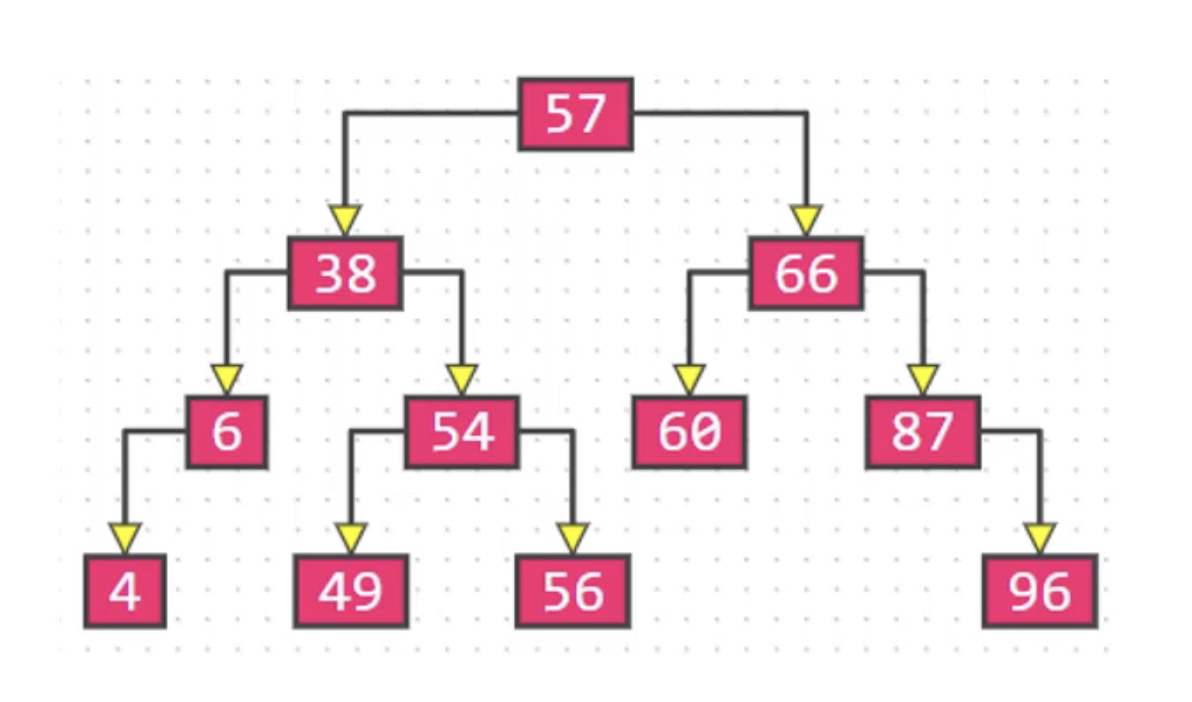
二叉树的特点：

• 每个节点的度最大为 2（最多拥有 2 棵子树）
• 左子树和右子树是有顺序的，二叉树是有序树
• 即使某节点只有一棵子树，也要区分左右子树

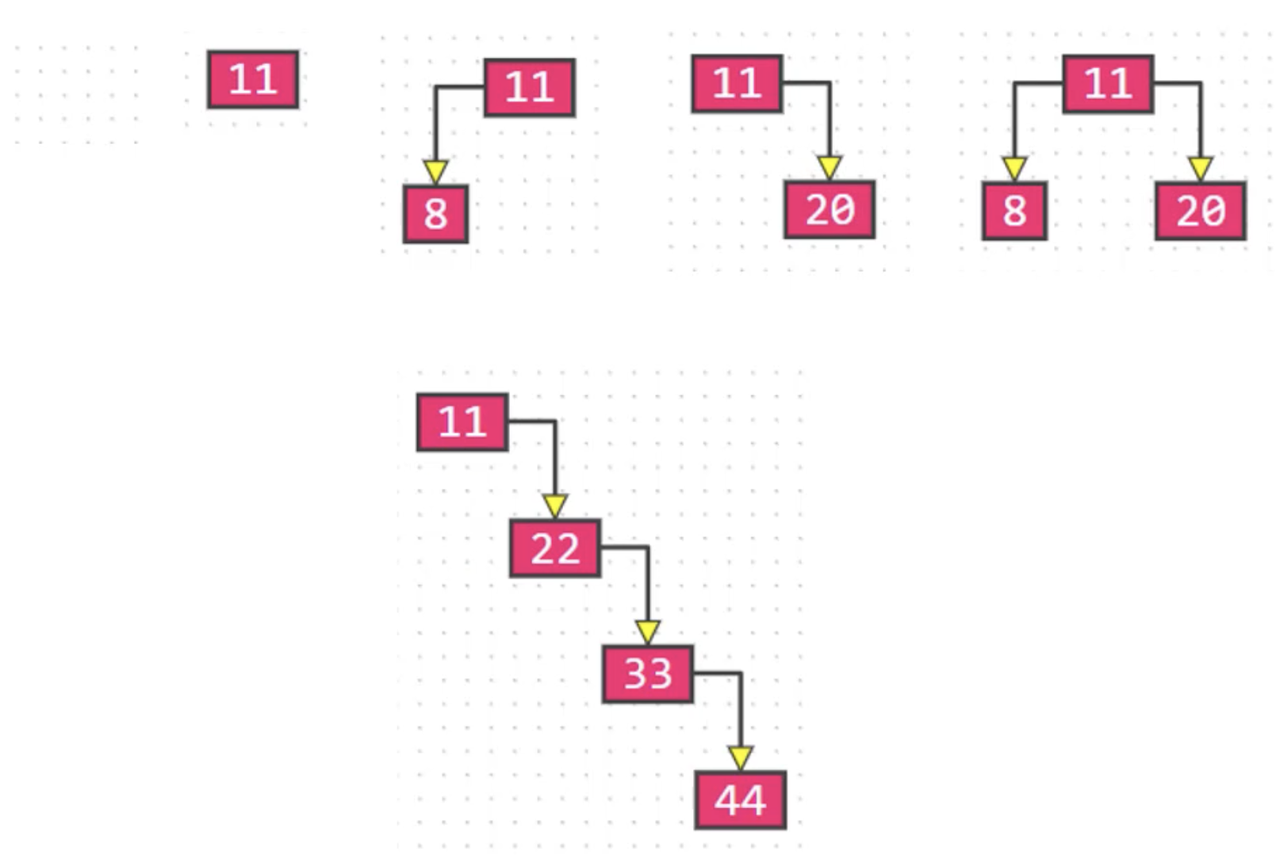
上面这几种都是二叉树

问题：二叉树是有序树 还是 无序树？

回答：二叉树是有序树，因为二叉树的左右子树是严格区分的，不能调换，所以二叉树是有序树

二叉树的性质

• 非空二叉树的第 i 层，最多有 2 ^ ( i - 1 ) 个节点（ i ≥ 1 ）
• 在高度为 h 的二叉树上最多有 2 ^ h - 1 个结点（ h ≥ 1 ）
• 对于任何一棵非空二叉树，如果叶子节点个数为 n0，度为 2 的节点个数为 n2，则有：n0 = n2 + 1
  • 假设度为 1 的节点个数为 n1，那么二叉树的节点总数 n = n0 + n1 + n2
  • 二叉树的边数 T = 1 * n1 + 2 * n2 = n – 1 = n0 + n1 + n2 – 1
  • 因此 n0 = n2 + 1

真二叉树（Proper Binary Tree）

真二叉树：所有节点的度都要么为 0，要么为 2

下图不是真二叉树：

满二叉树（Full Binary Tree）

满二叉树：最后一层节点的度为0，其他节点的度都为2

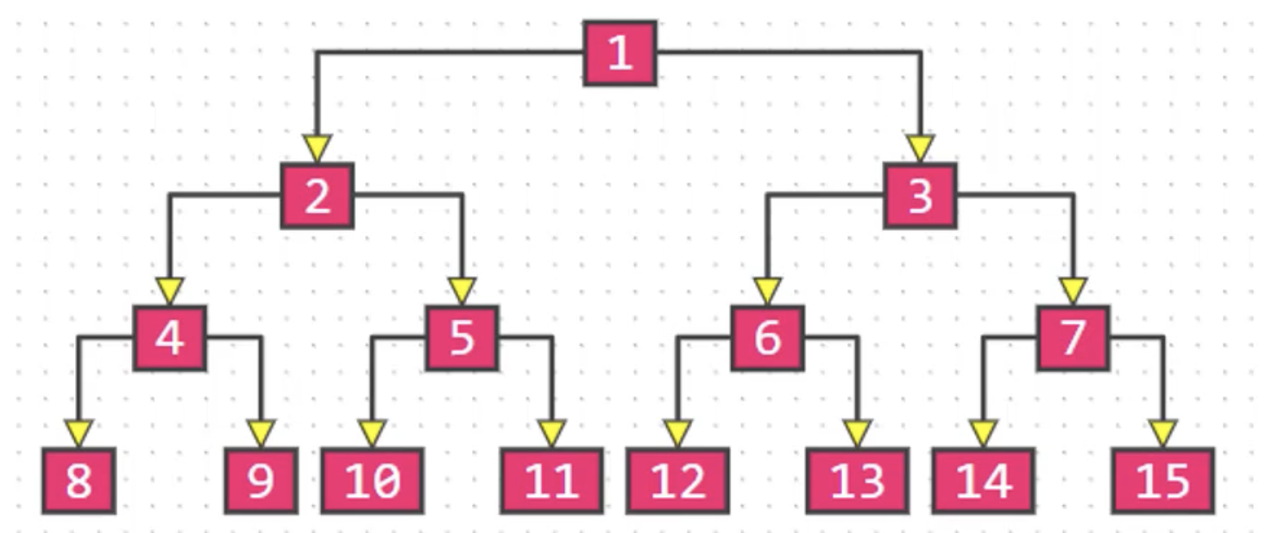
• 假设满二叉树的高度为 h（ h ≥ 1 ），那么
  • 第 i 层的节点数量： 2 ^ ( i ? 1 )
  • 叶子节点数量： 2 ^ ( h ? 1 )
  • 总节点数量: n
  • n = 2 ^ h ? 1 = 2^0 + 2^1 + 2^2 + ? + 2 ^ ( h ? 1 )
  • 树高度与总节点的关系：h = log2 (n + 1)

在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多

满二叉树一定是真二叉树，真二叉树不一定是满二叉树

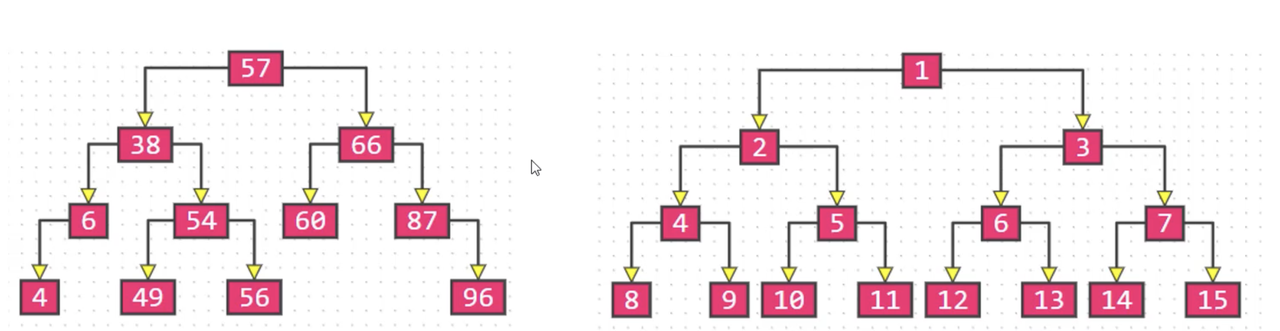
完全二叉树（Complete Binary Tree）

完全二叉树：对节点从上至下、左至右开始编号，其所有编号都能与相同高度的满二叉树中的编号对应

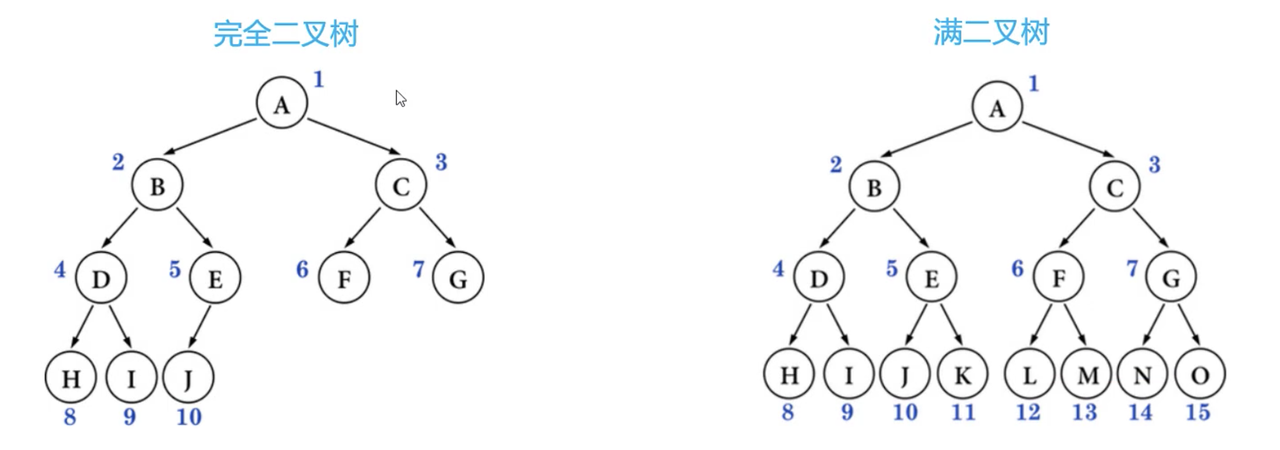
完全二叉树从根节点 至 倒数第2层是一棵满二叉树

满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

完全二叉树的性质

根节点从1开始编号

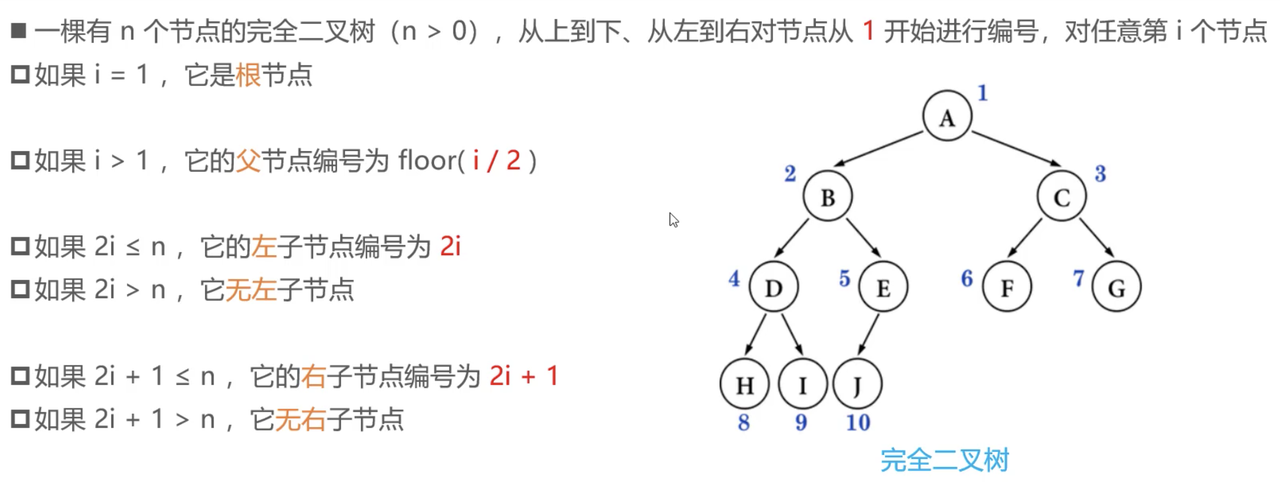
根节点从0开始编号

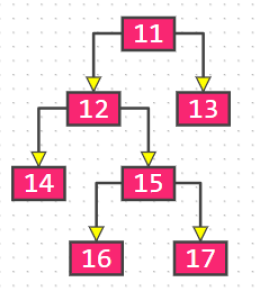
下图不是完全二叉树

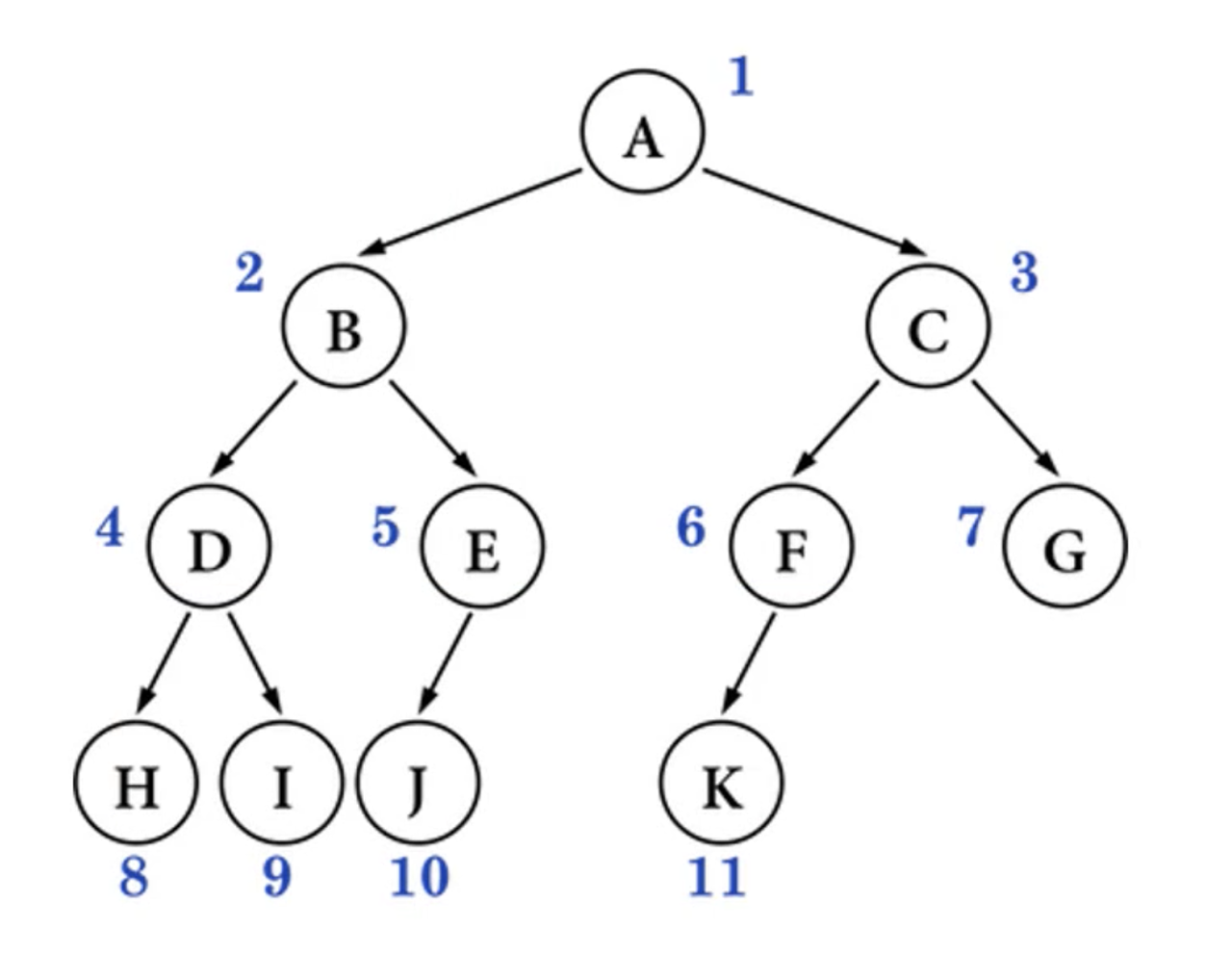
面试题（完全二叉树）

国外教材的说法（了解一下）

二叉树的遍历

• 遍历是数据结构中的常见操作

  • 把所有元素都访问一遍

• 线性数据结构的遍历比较简单：

  • 正序遍历
  • 逆序遍历

• 根据节点访问顺序的不同，二叉树的常见遍历方式有 4 种：

  • 前序遍历（Preorder Traversal）
  • 中序遍历（Inorder Traversal）
  • 后序遍历（Postorder Traversal）
  • 层序遍历（Level Order Traversal）

• 遍历的应用：

  • 前序遍历：树状结构展示（注意左右子树的顺序）
  • 中序遍历：二叉搜索树的中序遍历按升序或者降序处理节点
  • 后序遍历：适用于一些先子后父的操作
  • 层序遍历：计算二叉树的高度、判断一棵树是否为完全二叉树

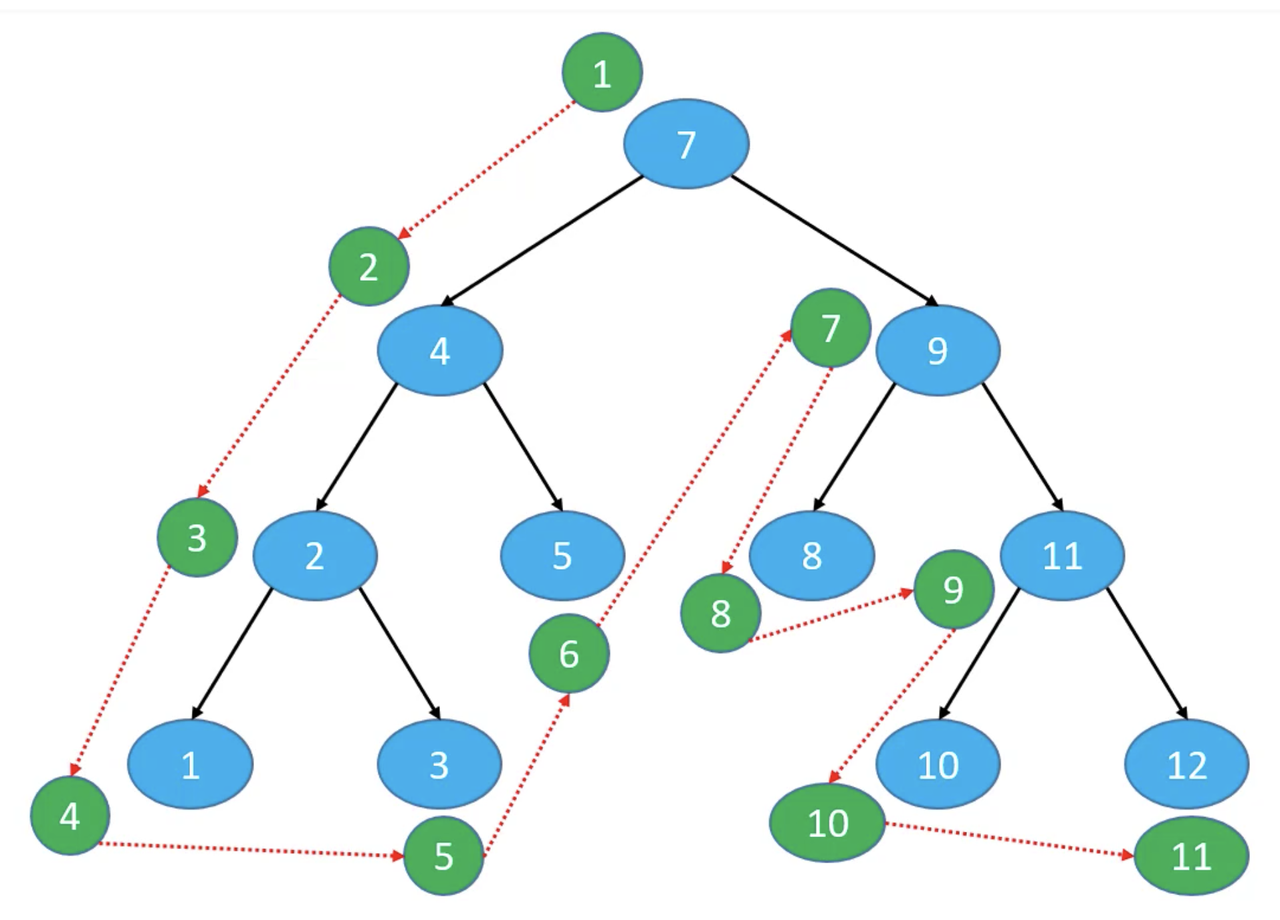
前序遍历（Preorder Traversal）

访问顺序：

根节点、前序遍历左子树、前序遍历右子树

下图前序遍历的结果是：7、4、2、1、3、5、9、8、11、10、12

/**
 * 前序遍历
 */
public void preorderTraversal() {
    preorderTraversal(root);
}

private void preorderTraversal(Node<E> node) {
    if (node == null) {
        return;
    }
    //先访问根节点
    System.out.println(node.element);
    //访问左子节点
    preorderTraversal(node.left);
    //访问右子节点
    preorderTraversal(node.right);
}

前序遍历 - 非递归

方法一

/**
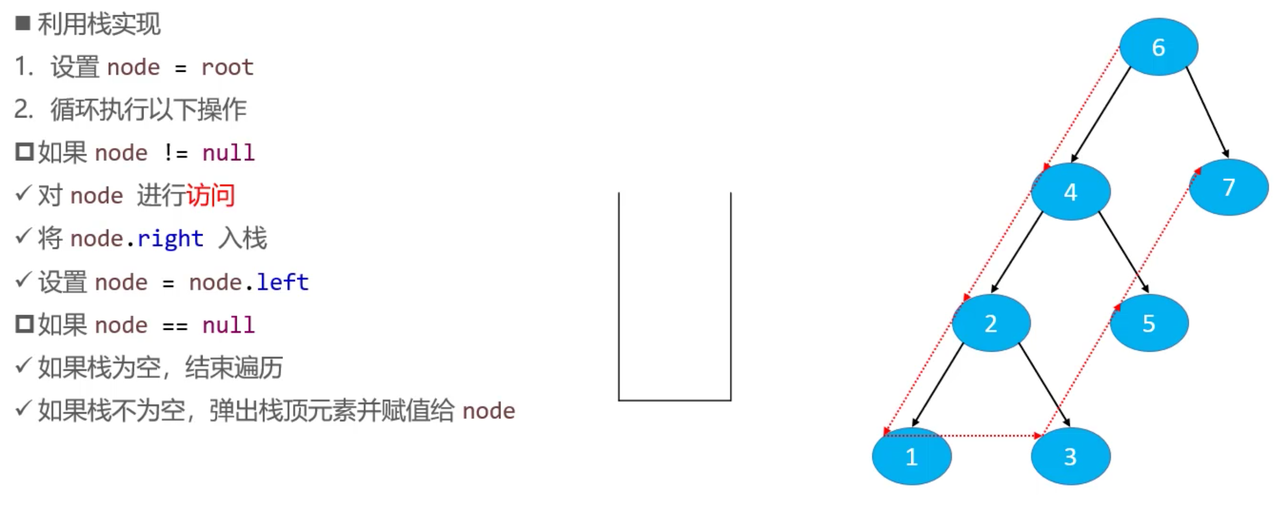
 * 前序遍历1
 *
 * @param visitor
 */
public void preorder2(Visitor<E> visitor) {
    if (visitor == null || root == null) {
        return;
    }
    Node<E> node = root;
    Stack<Node<E>> stack = new Stack<>();
    while (true) {
        if (node != null) {
            // 访问node节点
            if (visitor.visit(node.element)) { //如果返回值为true，停止遍历
                return;
            }
            // 将右子节点入栈
            if (node.right != null) {
                stack.push(node.right);
            }
            // 向左走
            node = node.left;
        } else if (stack.isEmpty()) { //栈为空，停止遍历
            return;
        } else { //node == null,栈不为空
            // 处理右边
            node = stack.pop();
        }
    }
}

方法二

/**
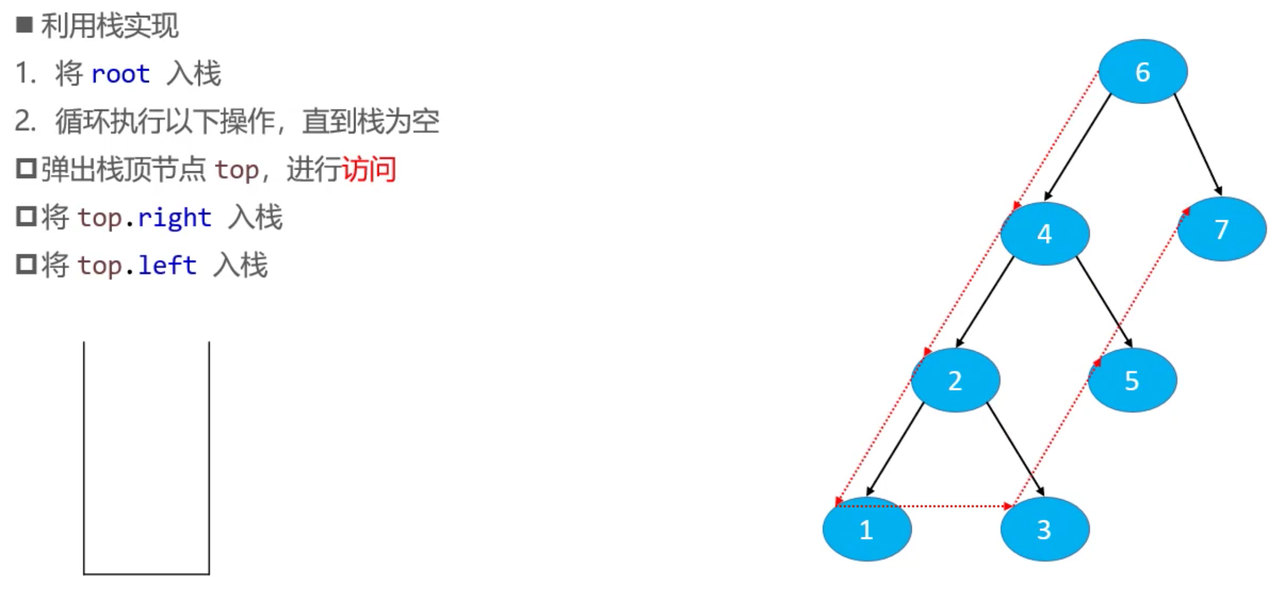
 * 前序遍历2
 *
 * @param visitor
 */
public void preorder(Visitor<E> visitor) {
    if (visitor == null || root == null) {
        return;
    }

    Stack<Node<E>> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        Node<E> node = stack.pop();
        // 访问node节点
        if (visitor.visit(node.element)) {
            return;
        }
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}

中序遍历（Inorder Traversal）

访问顺序：

中序遍历左子树、根节点、中序遍历右子树

下图中序遍历的结果是：1、2、3、4、5、7、8、9、10、11、12

二叉搜索树的中序遍历结果是升序或者降序的

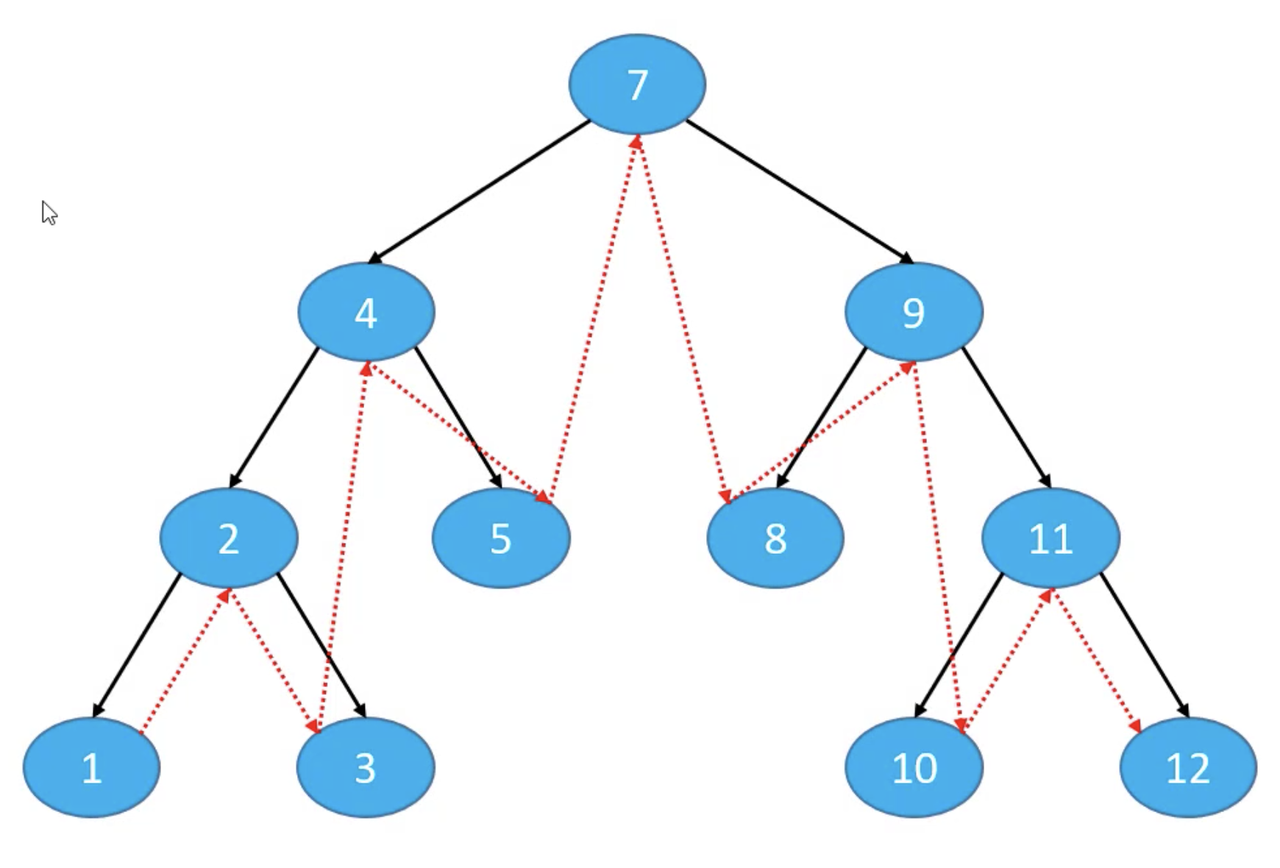
另一种中序遍历访问顺序：

中序遍历右子树、根节点、中序遍历左子树

则上图的中序遍历的结果是：12、11、10、9、8 、7、5、4、3、2、1

/**
 * 中序遍历
 */
public void inorderTraversal() {
    inorderTraversal(root);
}

private void inorderTraversal(Node<E> node) {
    if (node == null) {
        return;
    }
    //先中序遍历左子树
    inorderTraversal(node.left);
    //输出根节点
    System.out.println(node.element);
    //再中序遍历右子树
    inorderTraversal(node.right);
}

中序遍历 - 非递归

/**
 * 中序遍历 - 非递归
 *
 * @param visitor
 */
public void inorder(Visitor<E> visitor) {
    if (visitor == null || root == null) {
        return;
    }
    Node<E> node = root;
    Stack<Node<E>> stack = new Stack<>();
    while (true) {
        if (node != null) {
            // 入栈
            stack.push(node);
            // 向左走
            node = node.left;
        } else if (stack.isEmpty()) {
            return;
        } else {
            node = stack.pop();
            // 访问node节点
            if (visitor.visit(node.element)) {
                return;
            }
            // 让右节点进行中序遍历
            node = node.right;
        }
    }
}

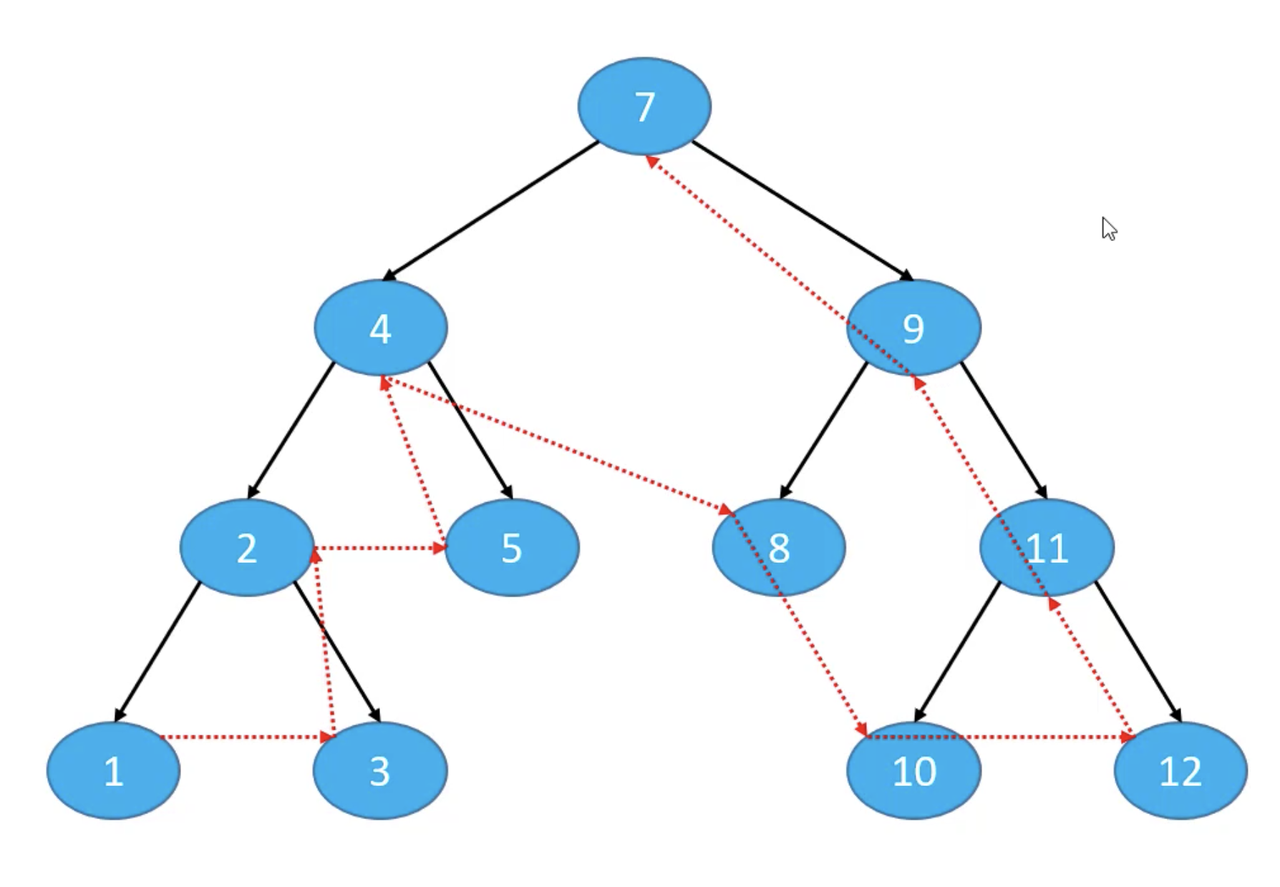
后序遍历（Postorder Traversal）

访问顺序：

后序遍历左子树、后序遍历右子树、根节点

下图的后序遍历的结果是：1、3、2、5、4、8、10、12、11、9、7

/**
 * 后序遍历
 */
public void postorderTraversal() {
    postorderTraversal(root);
}

private void postorderTraversal(Node<E> node) {
    if (node == null) {
        return;
    }
    //先遍历左子树
    postorderTraversal(node.left);
    //再遍历右子树
    postorderTraversal(node.right);
    //最后访问根节点
    System.out.println(node.element);
}

后序遍历 - 非递归

/**
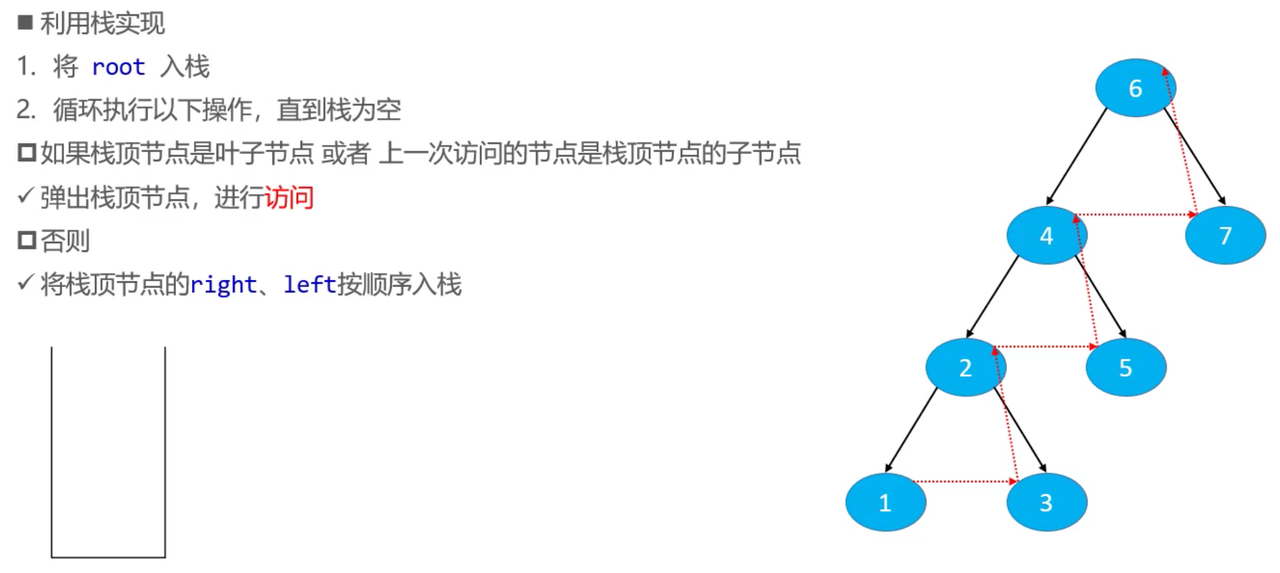
 * 后序遍历 - 非递归
 *
 * @param visitor
 */
public void postorder(Visitor<E> visitor) {
    if (visitor == null || root == null) {
        return;
    }
    // 记录上一次弹出访问的节点
    Node<E> prev = null;

    Stack<Node<E>> stack = new Stack<>();
    //将根节点入栈
    stack.push(root);
    while (!stack.isEmpty()) { //栈不为空
        Node<E> top = stack.peek(); //返回栈顶元素
        if (top.isLeaf() || (prev != null && prev.parent == top)) {
            prev = stack.pop();
            // 访问节点
            if (visitor.visit(prev.element)) {
                return;
            }
        } else {
            if (top.right != null) {
                stack.push(top.right); //将右节点入栈
            }
            if (top.left != null) {
                stack.push(top.left); //将左节点入栈
            }
        }
    }
}

层序遍历（Level Order Traversal）

访问顺序：

从上到下、从左到右依次访问每一个节点

下图的层序遍历的结果是：7、4、9、2、5、8、11、1、3、10、12

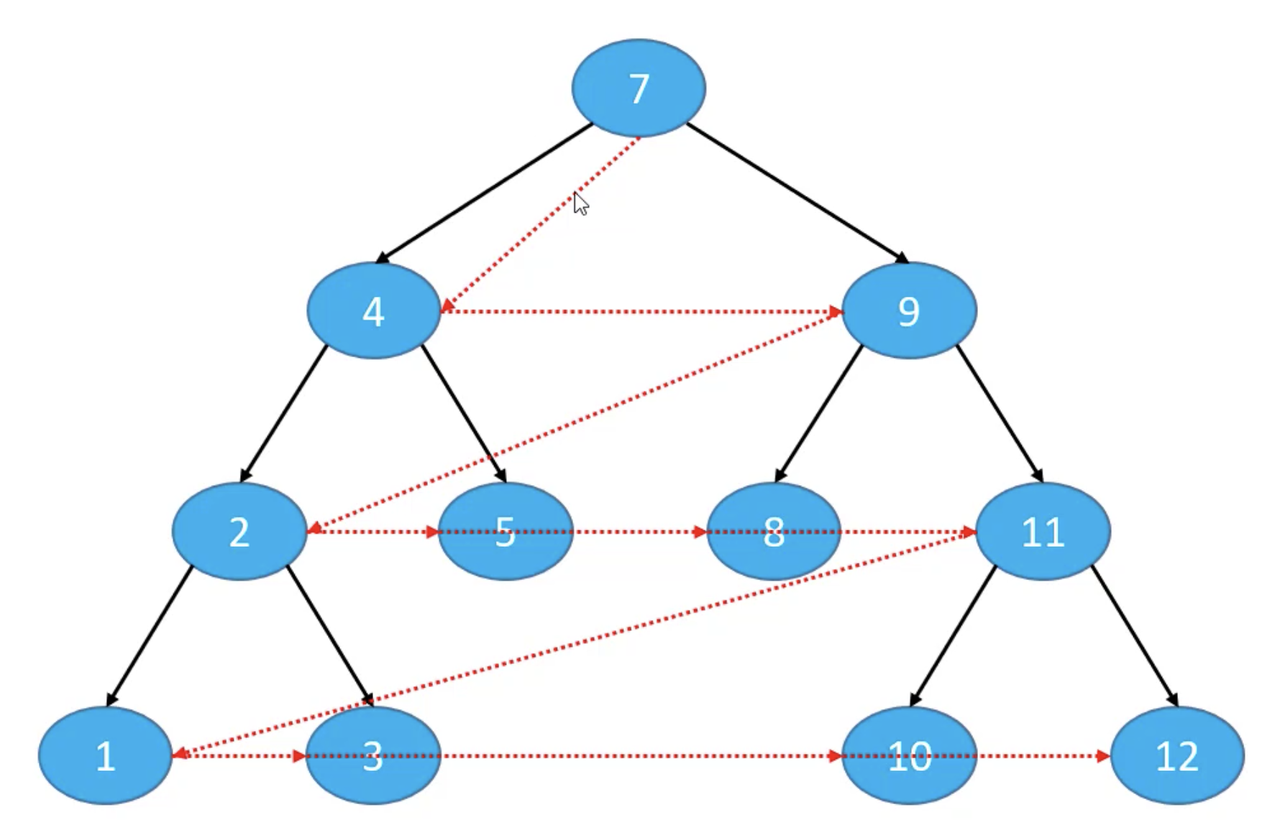
实现思路：使用队列

1. 将根节点入队

2. 循环执行以下操作，直到队列为空

   将队头节点A出队，进行访问

   将A的左子节点入队

   将A的右子节点入队

/**
 * 层序遍历
 */
public void levelOrderTranversal() {
    if (root == null) {
        return;
    }
    //新建一个队列
    Queue<Node<E>> queue = new LinkedList<>();
    //将头节点入队
    queue.offer(root);
    while (!queue.isEmpty()) {
        //将头结点出队
        Node<E> node = queue.poll();
        System.out.println(node.element);
        //如果左子节点不为空，就将左子节点入队
        if (node.left != null) {
            queue.offer(node.left);
        }
        //如果右子节点不为空，就将右子节点入队
        if (node.right != null) {
            queue.offer(node.right);
        }
    }
}

定制遍历接口

”可以定制输出的格式，首先得有个内部接口类

/**
 * Visitor 接口
 * @param <E>
 */
public static interface Visitor<E> {
    void visit(E element);
}

前序遍历接口

public void preorder(Visitor<E> visitor) {
    preorder(root, visitor);
}

private void preorder(Node<E> node, Visitor<E> visitor) {
    if (node == null || visitor == null) {
        return;
    }
    visitor.visit(node.element);
    preorder(node.left, visitor);
    preorder(node.right, visitor);
}

中序遍历接口

public void inorder(Visitor<E> visitor) {
    inorder(root, visitor);
}

private void inorder(Node<E> node, Visitor<E> visitor) {
    if (node == null || visitor == null) {
        return;
    }
    inorder(node.left, visitor);
    visitor.visit(node.element);
    inorder(node.right, visitor);
}

后序遍历接口

public void postorder(Visitor<E> visitor) {
    postorder(root, visitor);
}

private void postorder(Node<E> node, Visitor<E> visitor) {
    if (node == null || visitor == null) {
        return;
    }
    postorder(node.left, visitor);
    postorder(node.right, visitor);
    visitor.visit(node.element);
}

层序遍历接口

public void levelOrder(Visitor<E> visitor) {
    if (root == null || visitor == null) {
        return;
    }
    Queue<Node<E>> queue = new LinkedList<>();
    //将头节点入队
    queue.offer(root);
    while (!queue.isEmpty()) {
        //将头结点出队
        Node<E> node = queue.poll();
        visitor.visit(node.element);
        //如果左子节点不为空，就将左子节点入队
        if (node.left != null) {
            queue.offer(node.left);
        }
        //如果右子节点不为空，就将右子节点入队
        if (node.right != null) {
            queue.offer(node.right);
        }
    }
}

遍历的应用

前序遍历

树状结构展示（注意左右子树的顺序）

@Override
public String toString() {
    StringBuilder sb = new StringBuilder();
    toString(root, sb, "");
    return sb.toString();
}

private void toString(Node<E> node, StringBuilder sb, String prefix) {
    if (node == null) {
        return;
    }
    sb.append(prefix).append(node.element).append("\n");
    toString(node.left, sb, prefix + "L---");
    toString(node.right, sb, prefix + "R---");
}

中序遍历

二叉搜索树的中序遍历按升序或者降序处理节点

后序遍历

适用于一些先子后父的操作

层序遍历

计算二叉树的高度

判断一棵树是否为完全二叉树

练习

练习 - 计算二叉树的高度

递归解法

/**
 * 计算二叉树的高度
 *
 * @return
 */
public int height() {
    return height(root);
}

/**
 * 获取某一个节点的高度
 * 递归解法
 *
 * @param node
 * @return
 */
private int height(Node<E> node) {
    if (node == null) {
        return 0;
    }
    return 1 + Math.max(height(node.left), height(node.right));
}

迭代解法

/**
 * 计算二叉树的高度
 * 非递归解法
 */
public int height() {
    if (root == null) {
        return 0;
    }
    //树的高度
    int height = 0;
    //存储着每一层的元素数量
    int levelSize = 1;
    Queue<Node<E>> queue = new LinkedList<>();
    //将头节点入队
    queue.offer(root);
    while (!queue.isEmpty()) {
        //将头结点出队
        Node<E> node = queue.poll();
        levelSize--;
        //如果左子节点不为空，就将左子节点入队
        if (node.left != null) {
            queue.offer(node.left);
        }
        //如果右子节点不为空，就将右子节点入队
        if (node.right != null) {
            queue.offer(node.right);
        }
        if (levelSize == 0) { //意味着即将要访问下一层
            levelSize = queue.size();
            height++;
        }
    }
    return height;
}

练习 - 判断一棵树是否为完全二叉树

写法一 思路分析

• 如果树为空，返回 false
• 如果树不为空，开始层序遍历二叉树（用队列）
  • 如果 node.left != null && node.right != null，将 node.left、node.right 按顺序入队
  • 如果 node.left == null && node.right != null，返回 false
  • 如果 node.left != null && node.right == null 或者 node.left == null && node.right == null
    • 那么后面遍历的节点应该都为叶子节点，才是完全二叉树
    • 否则返回 false
  • 遍历结束，返回 true

/**
 * 判断这棵二叉树是不是完全二叉树
 */
public boolean isComplete() {
    if (root == null) {
        return false;
    }
    Queue<Node<E>> queue = new LinkedList<>();
    //将头节点入队
    queue.offer(root);

    boolean leaf = false;
    while (!queue.isEmpty()) {
        //将头结点出队
        Node<E> node = queue.poll();

        //要求是叶子节点，但这个节点却不是叶子节点
        if (leaf && !node.isLeaf()) {
            return false;
        }
        if (node.left != null && node.right != null) {
            queue.offer(node.left);
            queue.offer(node.right);
        } else if (node.left == null && node.right != null) {
            return false;
        } else { //后面遍历的节点都必须是叶子节点
            leaf = true;
            if (node.left != null) {
                queue.offer(node.left);
            }
        }
    }
    return true;
}

写法二思路分析：推荐

• 如果树为空，返回 false
• 如果树不为空，开始层序遍历二叉树（用队列）
  • 如果 node.left != null，将 node.left 入队
  • 如果 node.left == null && node.right != null，返回 false
  • 如果 node.right != null，将 node.right 入队
  • 如果 node.right == null
    • 那么后面遍历的节点应该都为叶子节点，才是完全二叉树
    • 否则返回 false
  • 遍历结束，返回 true

/**
 * 判断这棵二叉树是不是完全二叉树
 */
public boolean isComplete() {
    if (root == null) {
        return false;
    }
    Queue<Node<E>> queue = new LinkedList<>();
    //将头节点入队
    queue.offer(root);

    boolean leaf = false;
    while (!queue.isEmpty()) {
        //将头结点出队
        Node<E> node = queue.poll();
        //要求是叶子节点，但这个节点却不是叶子节点
        if (leaf && !node.isLeaf()) {
            return false;
        }

        if (node.left != null) {
            queue.offer(node.left);
        } else if (node.right != null) {
            //node.left == null && node.right != null
            return false;
        }

        if (node.right != null) {
            queue.offer(node.right);
        } else {
            //包含下面两种情况
            //node.left == null && node.right == null
            //node.left != null && node.right == null
            leaf = true;
        }
    }
    return true;
}

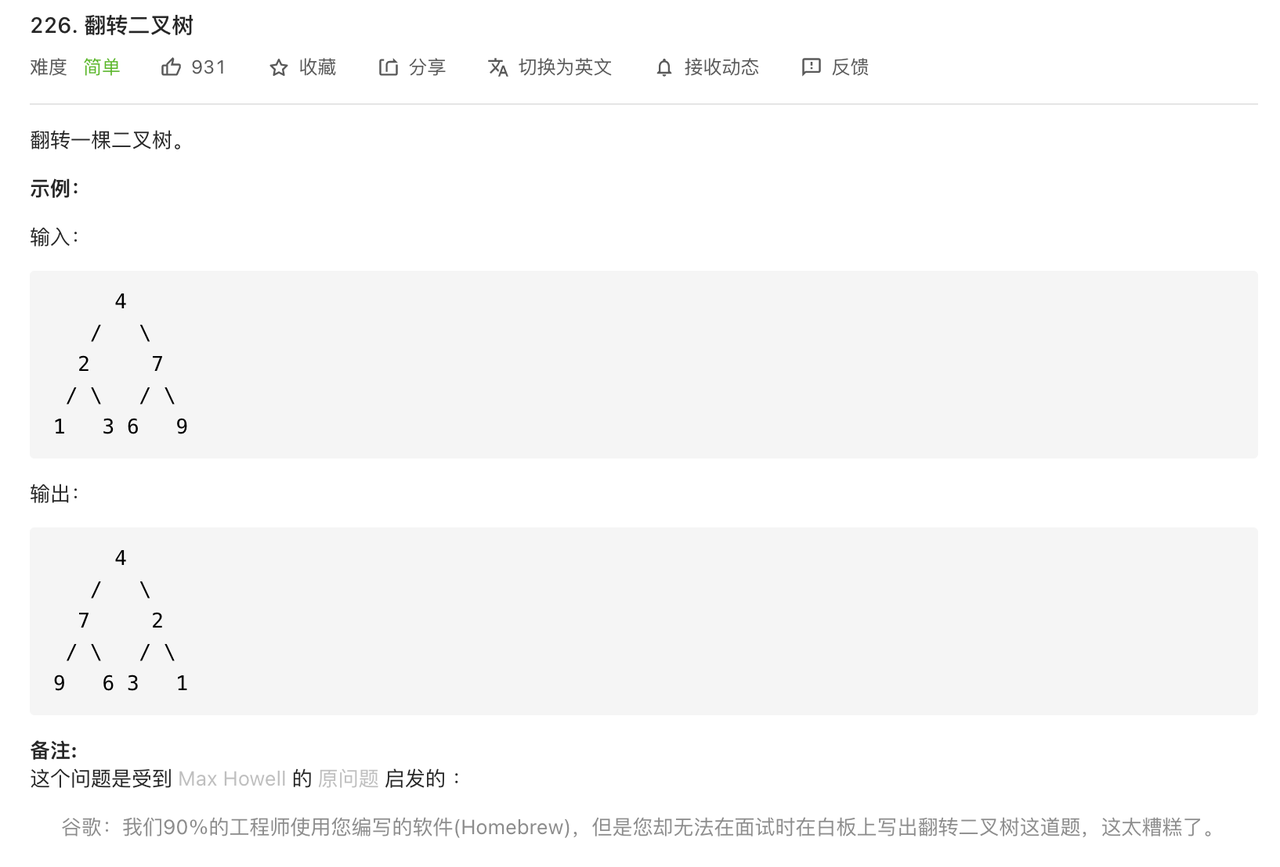
练习 - 翻转二叉树

226_翻转二叉树：https://leetcode-cn.com/problems/invert-binary-tree/

解法一：前序遍历

package 二叉树;

/**
 * https://leetcode-cn.com/problems/invert-binary-tree/
 *
 * @author xiexu
 * @create 2021-07-30 6:56 下午
 */
public class _226_翻转二叉树 {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        //交换左右子树
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

解法二：后序遍历

package 二叉树;

/**
 * https://leetcode-cn.com/problems/invert-binary-tree/
 *
 * @author xiexu
 * @create 2021-07-30 6:56 下午
 */
public class _226_翻转二叉树 {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }

        invertTree(root.left);
        invertTree(root.right);

        //交换左右子树
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        return root;
    }
}

解法三：类似于中序遍历，但要注意交换后的左右子树顺序

package 二叉树;

/**
 * https://leetcode-cn.com/problems/invert-binary-tree/
 *
 * @author xiexu
 * @create 2021-07-30 6:56 下午
 */
public class _226_翻转二叉树 {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }

        invertTree(root.left);

        //交换左右子树
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        invertTree(root.left);

        return root;
    }
}

解法四：层序遍历

package 二叉树;

import java.util.LinkedList;
import java.util.Queue;

/**
 * https://leetcode-cn.com/problems/invert-binary-tree/
 *
 * @author xiexu
 * @create 2021-07-30 6:56 下午
 */
public class _226_翻转二叉树 {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            TreeNode tmp = node.left;
            node.left = node.right;
            node.right = tmp;

            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        return root;
    }
}

根据遍历结果重构二叉树

• 以下结果可以保证重构出唯一的一棵二叉树：
  • 前序遍历 + 中序遍历
  • 后序遍历 + 中序遍历

前序遍历+中序遍历 重构二叉树

• 前序遍历 + 后序遍历：
  • 如果它是一棵真二叉树（Proper Binary Tree），结果是唯一的
• 不然结果不唯一

求二叉树的节点

前驱节点（predecessor）

/**
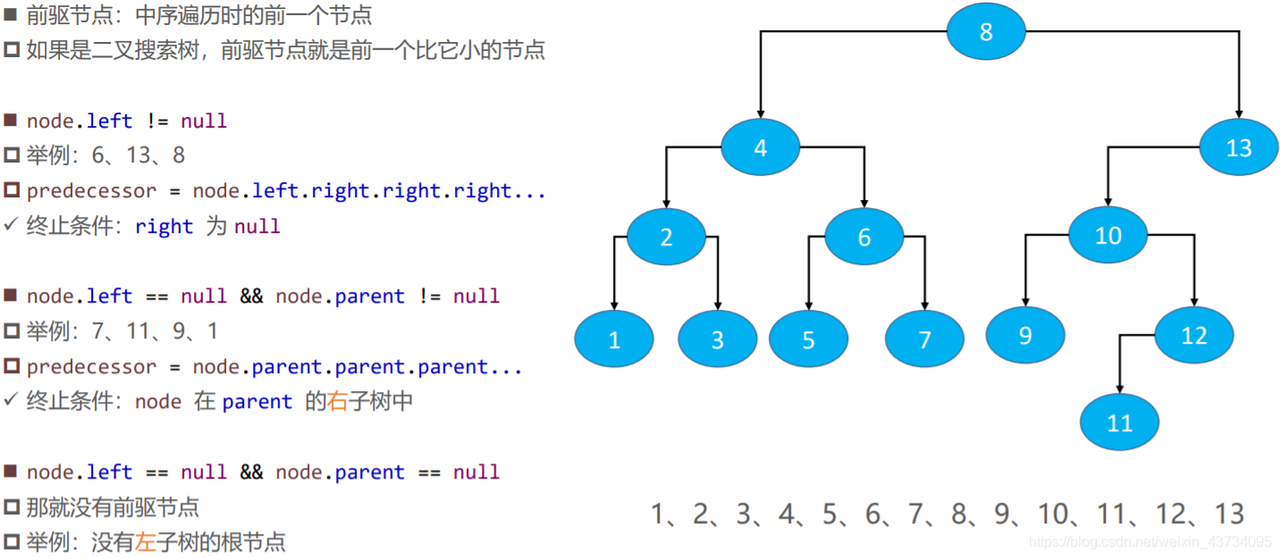
 * 前驱节点: 中序遍历时的前一个节点
 * 求前驱节点
 */
private Node<E> predecessor(Node<E> node) {
    if (node == null) {
        return null;
    }
    //前驱节点在左子树中(left.right.right.right....)
    Node<E> p = node.left;
    if (node.left != null) {
        //左子树不为空，则找到它的最右节点
        while (p.right != null) {
            p = p.right;
        }
        return p;
    }

    // 能来到这里说明左子树为空, 则从父节点、祖父节点中寻找前驱节点
    // 当父节点不为空, 且某节点为父节点的左子节点
    // 则顺着父节点找, 直到找到【某结点为父节点或祖父节点的右子树中】时
    while (node.parent != null && node.parent.left == node) {
        node = node.parent;
    }

    // 来到这里有以下两种情况:
    // node.parent == null 无前驱, 说明是根结点
    // node.parent...right == node 找到【某结点为父节点或祖父节点的右子树中】
    // 那么父节点就是某节点的前驱节点
    return node.parent;
}

后继节点（successor）

/**
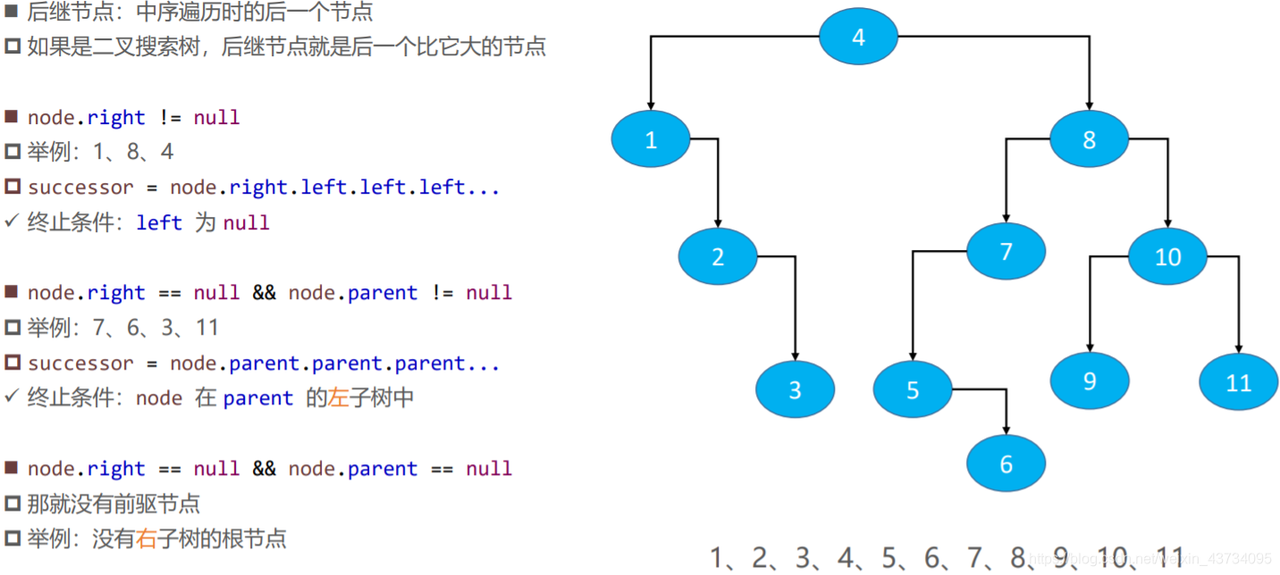
 * 后继节点: 中序遍历时的后一个节点
 * 求后继节点
 */
private Node<E> successor(Node<E> node) {
    if (node == null) {
        return null;
    }
    //后继节点在右子树中(right.left.left.left....)
    Node<E> p = node.right;
    if (node.right != null) {
        //左子树不为空，则找到它的最右节点
        while (p.left != null) {
            p = p.left;
        }
        return p;
    }

    // 能来到这里说明右子树为空, 则从父节点、祖父节点中寻找后继节点
    // 当父节点不为空, 且某节点为父节点的右子节点
    // 则顺着父节点找, 直到找到【某结点为父节点或祖父节点的左子树中】时
    while (node.parent != null && node.parent.right == node) {
        node = node.parent;
    }

    // 来到这里有以下两种情况:
    // node.parent == null 无后继, 说明是根结点
    // node.parent...left == node 找到【某结点为父节点或祖父节点的左子树中】
    // 那么父节点就是某节点的后继节点
    return node.parent;
}

BinaryTreeInfo 工具

这是小码哥自己写的一款工具，可以方便的打印二叉树，github 地址如下：https://github.com/CoderMJLee/BinaryTrees。

/**
 * BinaryTreeInfo 工具，用来打印二叉树
 */
@Override
public Object root() {
        return root;
}
@Override
public Object left(Object node) {
        return ((Node<E>)node).left;
}
@Override
public Object right(Object node) {
        return ((Node<E>)node).right;
}
@Override
public Object string(Object node) {
        Node<E> myNode = (Node<E>)node;
        String parentStr = "null";
        if(myNode.parent != null){
                parentStr = myNode.parent.element.toString();
        }
        return myNode.element + "_p(" + parentStr + ")";
}

二叉树完整源码

package cn.xx.java.tree;

import cn.xx.java.printer.BinaryTreeInfo;

import java.util.LinkedList;
import java.util.Queue;

/**
 * 二叉树
 * @author xiexu
 * @create 2021-08-02 12:14 下午
 */
public class BinaryTree<E> implements BinaryTreeInfo {
    protected int size; //节点数量
    protected Node<E> root; //根节点

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public void clear() {
        root = null;
        size = 0;
    }

    protected static class Node<E> {
        E element;
        Node<E> left; //左子节点
        Node<E> right; //右子节点
        Node<E> parent; //父节点

        public Node(E element, Node<E> parent) {
            this.element = element;
            this.parent = parent;
        }

        //判断当前节点是不是叶子节点
        public boolean isLeaf() {
            return left == null && right == null;
        }

        //判断当前节点是不是拥有两个子节点
        public boolean hasTwoChildren() {
            return left != null && right != null;
        }
    }

    public static interface Visitor<E> {
        void visit(E element);
    }

    /**
     * 前序遍历
     * @param visitor
     */
    public void preorder(Visitor<E> visitor) {
        preorder(root, visitor);
    }

    private void preorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor == null) {
            return;
        }
        visitor.visit(node.element);
        preorder(node.left, visitor);
        preorder(node.right, visitor);
    }

    /**
     * 中序遍历
     * @param visitor
     */
    public void inorder(Visitor<E> visitor) {
        inorder(root, visitor);
    }

    private void inorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor == null) {
            return;
        }
        inorder(node.left, visitor);
        visitor.visit(node.element);
        inorder(node.right, visitor);
    }

    /**
     * 后序遍历
     * @param visitor
     */
    public void postorder(Visitor<E> visitor) {
        postorder(root, visitor);
    }

    private void postorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor == null) {
            return;
        }
        postorder(node.left, visitor);
        postorder(node.right, visitor);
        visitor.visit(node.element);
    }

    /**
     * 层序遍历
     * @param visitor
     */
    public void levelOrder(Visitor<E> visitor) {
        if (root == null || visitor == null) {
            return;
        }
        Queue<Node<E>> queue = new LinkedList<>();
        //将头节点入队
        queue.offer(root);
        while (!queue.isEmpty()) {
            //将头结点出队
            Node<E> node = queue.poll();
            visitor.visit(node.element);
            //如果左子节点不为空，就将左子节点入队
            if (node.left != null) {
                queue.offer(node.left);
            }
            //如果右子节点不为空，就将右子节点入队
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

    @Override
    public Object root() {
        return root;
    }

    @Override
    public Object left(Object node) {
        return ((Node<E>) node).left;
    }

    @Override
    public Object right(Object node) {
        return ((Node<E>) node).right;
    }

    @Override
    public Object string(Object node) {
        Node<E> myNode = (Node<E>) node;
        String parentString = "null";
        if (myNode.parent != null) {
            parentString = myNode.parent.element.toString();
        }
        return ((Node<E>) node).element + "_p(" + parentString + ")";
    }

    /**
     * 前驱节点: 中序遍历时的前一个节点
     * 求前驱节点
     */
    protected Node<E> predecessor(Node<E> node) {
        if (node == null) {
            return null;
        }
        //前驱节点在左子树中(left.right.right.right....)
        Node<E> p = node.left;
        if (node.left != null) {
            //左子树不为空，则找到它的最右节点
            while (p.right != null) {
                p = p.right;
            }
            return p;
        }

        // 能来到这里说明左子树为空, 则从父节点、祖父节点中寻找前驱节点
        // 当父节点不为空, 且某节点为父节点的左子节点
        // 则顺着父节点找, 直到找到【某结点为父节点或祖父节点的右子树中】时
        while (node.parent != null && node.parent.left == node) {
            node = node.parent;
        }

        // 来到这里有以下两种情况:
        // node.parent == null 无前驱, 说明是根结点
        // node.parent...right == node 找到【某结点为父节点或祖父节点的右子树中】
        // 那么父节点就是某节点的前驱节点
        return node.parent;
    }

    /**
     * 后继节点: 中序遍历时的后一个节点
     * 求后继节点
     */
    protected Node<E> successor(Node<E> node) {
        if (node == null) {
            return null;
        }
        //后继节点在右子树中(right.left.left.left....)
        Node<E> p = node.right;
        if (node.right != null) {
            //左子树不为空，则找到它的最右节点
            while (p.left != null) {
                p = p.left;
            }
            return p;
        }

        // 能来到这里说明右子树为空, 则从父节点、祖父节点中寻找后继节点
        // 当父节点不为空, 且某节点为父节点的右子节点
        // 则顺着父节点找, 直到找到【某结点为父节点或祖父节点的左子树中】时
        while (node.parent != null && node.parent.right == node) {
            node = node.parent;
        }

        // 来到这里有以下两种情况:
        // node.parent == null 无后继, 说明是根结点
        // node.parent...left == node 找到【某结点为父节点或祖父节点的左子树中】
        // 那么父节点就是某节点的后继节点
        return node.parent;
    }

    /**
     * 计算二叉树的高度
     * 非递归解法
     */
    public int height() {
        if (root == null) {
            return 0;
        }
        //树的高度
        int height = 0;
        //存储着每一层的元素数量
        int levelSize = 1;
        Queue<Node<E>> queue = new LinkedList<>();
        //将头节点入队
        queue.offer(root);
        while (!queue.isEmpty()) {
            //将头结点出队
            Node<E> node = queue.poll();
            levelSize--;
            //如果左子节点不为空，就将左子节点入队
            if (node.left != null) {
                queue.offer(node.left);
            }
            //如果右子节点不为空，就将右子节点入队
            if (node.right != null) {
                queue.offer(node.right);
            }
            if (levelSize == 0) { //意味着即将要访问下一层
                levelSize = queue.size();
                height++;
            }
        }
        return height;
    }

    /**
     * 计算二叉树的高度
     * 递归解法
     *
     * @return
     */
    public int height2() {
        return height(root);
    }

    /**
     * 获取某一个节点的高度
     * 递归解法
     *
     * @param node
     * @return
     */
    private int height(Node<E> node) {
        if (node == null) {
            return 0;
        }
        return 1 + Math.max(height(node.left), height(node.right));
    }

    /**
     * 判断这棵二叉树是不是完全二叉树
     */
    public boolean isComplete() {
        if (root == null) {
            return false;
        }
        Queue<Node<E>> queue = new LinkedList<>();
        //将头节点入队
        queue.offer(root);

        boolean leaf = false;
        while (!queue.isEmpty()) {
            //将头结点出队
            Node<E> node = queue.poll();
            //要求是叶子节点，但这个节点却不是叶子节点
            if (leaf && !node.isLeaf()) {
                return false;
            }

            if (node.left != null) {
                queue.offer(node.left);
            } else if (node.right != null) {
                //node.left == null && node.right != null
                return false;
            }

            if (node.right != null) {
                queue.offer(node.right);
            } else {
                //包含下面两种情况
                //node.left == null && node.right == null
                //node.left != null && node.right == null
                leaf = true;
            }
        }
        return true;
    }

}