在这个专栏中,博主将和苏苏一起,将《python数据结构与算法分析》一书中的重点内容总结出来。这是该专栏的第一篇,更多的内容将在后续更新。

一.异序词检测实例
如果一个字符串只是重排了另一个字符串的字符,那么这个字符串就是另一个的异序词,比如 heart 与 earth,以及 python 与yphon。
为了简化问题,假设要检查的两个字符串长度相同,并且都是由 26 个英文字母的小写形式组成的。我们的目标是编写一个布尔函数,它接受两个字符串,并能判断它们是否为异序词。
方案1:清点法
清点第 1 个字符串的每个字符,看看它们是否都出现在第 2 个字符串中。如果是,那么两个字符串必然是异序词。清点是通过用 Python 中的特殊值 None 取代字符来实现的。但是,因为Python 中的字符串是不可修改的,所以先要将第 2 个字符串转换成列表。字符列表中检查第 1个字符串中的每个字符,如果找到了,就替换掉。
def anagramSolution1(s1, s2):
alist = list(s2)
#检查第一个字符串的下标
pos1 = 0
stillOK = True
while pos1 < len(s1) and stillOK:
#检查第二个字符串的下标
pos2 = 0
found = False
while pos2 < len(alist) and not found:
if s1[pos1] == alist[pos2]:
found = True
else:
pos2 = pos2 + 1
if found:
alist[pos2] = None
else:
stillOK = False
pos1 = pos1 + 1
return stillOK
方案2:排序法
尽管 s1 与 s2 是不同的字符串,但只要由相同的字符构成,它们就是异序词。基于这一点,如果按照字母表顺序给字符排序,异序词得到的结果将是同一个字符串。
def anagramSolution2(s1, s2):
alist1=list(s1)
alist2=list(s2)
alist1.sort()
alist2.sort()
pos=0
matches=True
while pos<len(s1) and matches:
if alist1[pos]==alist2[pos]:
pos+=1
else:
matches=False
return matches
方案3:计数法
两个异序词有同样数目的 a、同样数目的 b、同样数目的 c,等等。要判断两个字符串是否为异序词,先数一下每个字符出现的次数。因为字符可能有26 种,所以使用 26 个计数器,对应每个字符。每遇到一字符,就将对应的计数器加 1。最后,如果两个计数器列表相同,那么两个字符串肯定是异序词。
def anagramSolution3(s1, s2):
c1=[0]*26
c2=[0]*26
for i in range(len(s1)):
#ord()函数是获取对应字符的ASCII值
pos=ord(s1[i])-ord('a')
c1[pos]+=1
for i in range(len(s2)):
pos=ord(s1[i])-ord('a')
c2[pos]+=1
j=0
stillOK = True
while j<26:
if c1[j]==c2[j]:
j+=1
else:
stillOK=False
return stillOK

二.python的基础数据结构
1.列表
假设要从 0 开始生成含有 n 个数的列表,来看看 4 种生成方式。首先,用 for
循环通过连接操作创建列表;其次,采用追加方法;再次,使用列表解析式。最后,用列表构造器调用 range函数
def test1():
l=[]
for i in range(1000):
l=l+[i]
def test2():
l=[]
for i in range(1000):
#在末尾插入
#insert()函数在指定的位置插入
l.append(i)
def test3():
l=[i for i in range(1000)]
def test4():
l=list[range(1000)]
栈
栈有时也被称作“下推栈”。它是有序集合,添加操作和移除操作总发生在同一端,即“顶端”,另一端则被称为“底端”。
栈中的元素离底端越近,代表其在栈中的时间越长,因此栈的底端具有非常重要的意义。最新添加的元素将被最先移除。这种排序原则被称作 LIFO(
last-in first-out),即后进先出。它提供了一种基于在集合中的时间来排序的方式。最近添加的元素靠近顶端,旧元素则靠近底端。

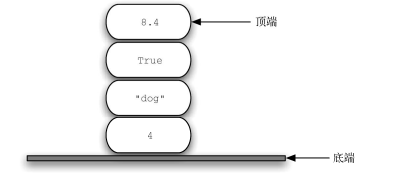
观察元素的添加顺序和移除顺序,就能理解栈的重要思想。假设桌面一开始是空的,每次只往桌上放一本书。如此堆叠,便能构建出一个栈。取书的顺序正好与放书的顺序相反。
栈抽象数据类型
抽象数据类型由下面的结构和操作定义。如前所述,栈是元素的有序集合,添加操作与移除操作都发生在其顶端。栈的操作顺序是
LIFO,它支持以下操作。
? Stack()创建一个空栈。它不需要参数,且会返回一个空栈。
? push(item)将一个元素添加到栈的顶端。它需要一个参数 item,且无返回值。
? pop()将栈顶端的元素移除。它不需要参数,但会返回顶端的元素,并且修改栈的内容。
? peek()返回栈顶端的元素,但是并不移除该元素。它不需要参数,也不会修改栈的内容。
? isEmpty()检查栈是否为空。它不需要参数,且会返回一个布尔值。
? size()返回栈中元素的数目。它不需要参数,且会返回一个整数。
用python语言实现栈
class Stack():
def __init__(self):
#返回一个空栈
self.items=[]
def isEmpty(self):
return self.items==[]
def push(self,item):
#在末尾插入
#insert()函数可以在指定的位置插入
#insert(len(self.items)-1,item)
self.items.append(item)
def pop(self):
#pop()函数返回最后一个元素
return self.items.pop()
#返回栈顶元素
def peek(self):
return self.items[(len(self.items)-1)]
def size(self):
return len(self.items)

三.今日题目
1.括号匹配
下面是正确匹配的括号串。
( ( ) ( ) ( )( ) )
( ( ( ( ) ) ) )
( ( ) ( ( () ) ( ) ) )
下面的这些括号则是不匹配的。
( ( ( ( ( ( ( ) )
( ) ) )
( ( ) ( ) ( ( )
我们的挑战就是编写一个算法,它从左到右读取个括号串,然后判断其中的括号是否匹配。
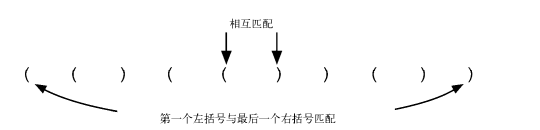
这个题目的经典解法就是利用栈。当出现左括号的时候,就压入栈中。当遇见右括号的时候,就出栈,看是否与右括号匹配。
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == "(":
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
s.pop()
index = index + 1
if balanced and s.isEmpty():
return True
else:
return False
将十进制转换为二进制
方法:模拟除K取余法

def divideBy2(decNumber):
remstack = Stack()
while decNumber > 0:
rem = decNumber % 2
remstack.push(rem)
decNumber = decNumber // 2
binString = ""
while not remstack.isEmpty():
binString = binString + str(remstack.pop())
return binString
