想说的话
大家好🌼🌼,我是 @愿此后再无WA,可以叫我小A,也可以叫我愿愿💡💡,一位阳光帅小伙,对算法领域比较感兴趣。如果我的文章对您有用,欢迎持续关注,我们一起进步!🎈🎈
很抱歉各位😪😪,现离蓝桥杯比赛不到一个月时间,我临时改变了计划,转为全心备战蓝桥,因为这个省一对我来说太重要了,也是我最后一次机会,我一定要拿到手📌📌,那么这样的话我在博客上花的时间就会少了很多,也将导致博客文章质量明显下降,在此我给大家说声抱歉💥💥
🌟🌟这些日子我真的很开心,博客上能遇到一群志同道合的兄弟姐妹真的很幸福,没有你们的支持与鼓励我早就坚持不下去了,因为有你们我才能走的更远????熬过这段时期我一定会回来的,爱你们????
题目
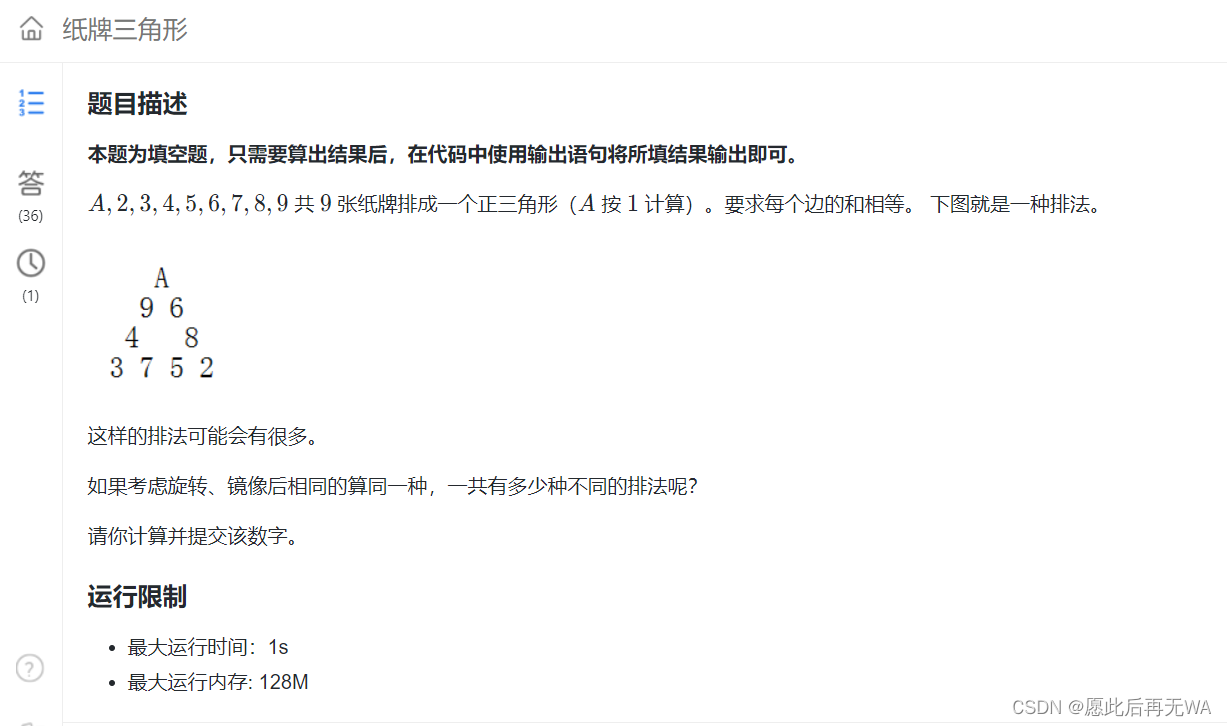
思路
这是一道填空题,数字区间不大,竞赛的时候想都别想直接全排列所有组合然后计算符合条件的结果即可。但是,现在不是比赛,我们就尽可能地利用平时使用的算法来优化解决以上问题,达到加深印象的目的。
我们先分析一下这个三角形有什么规律。可以知道处在顶点的三个数字出现过两次。所以总和其实就是1 ~ 9的和加上重复出现的三个数字的和。
对于一个等边三角形,他们三边之和一定是3的倍数。所以我们可以先计算这些数字的总和,判断是否能够整除3,如果可以,那么这些数字才有可能拼成等边三角形。”为什么是有可能而不是一定?因为一条边不能够出现两次相同的数字,顶点数字只会在两边出现而不是集中在一条边。
因此,我们可以回溯在9位数中找出三位数然后加上1 ~ 9的和(45)。然后筛选出有可能凑出等边三角形的数字即可,只需要找三个数字。
接着就是看能不能够凑出等边三角形了,我们可以通过数字总和除以3得出每条边的长度(d),因为三个顶点已经列举出来了,所以是已知的,我们就要在剩下的6个数中判断是否能与其中两个顶点凑出两条长度为d的边来,然后就将结果保存下来。(凑数的话当然就是用dp了)
还有最后一步。

题目说旋转镜像算同一种,因此,不考虑边上元素的话,顶点位置变化与否都是属于同一种排法。所以只能看边上的元素。
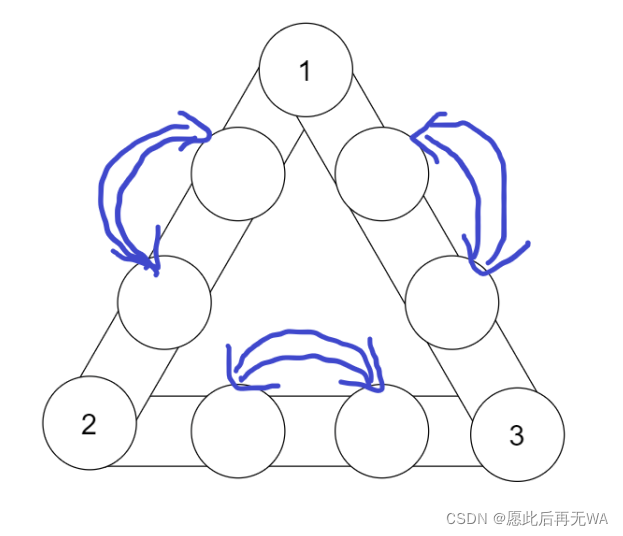
而边上的元素两两交换不会重复,所以每条边有两种排列,那么三条边就有222等于8种了。因此,最后要将结果乘上8.
代码
# 回溯
def dfs(start,cnt,s):
if cnt == 3:
if (s + 45) % 3 == 0 : # 能整除3才有可能出现3条相等的边
if is_eqtri((s+45)//3):
result[0] += 1
return
for i in range(start,length):
s += nums[i]
res.append(nums[i])
start += 1
dfs(start,cnt+1,s)
s -= nums[i] # start 不用减,因为出现过的不用再出现了,不必回头
res.pop()
# 凑数
def is_eqtri(slen):
ind = 0
tar1 = slen - (res[0] + res[2])
tar2 = slen - (res[1] + res[2])
tar3 = slen - (res[1] + res[0])
r = max(tar1,tar2,tar3) # 看三边中最长还差多少
dp = [False for i in range(r+1)]
for i in range(6): # 只要能拼出其中两条边就OK了,两条边能求出,第三条边必定能求出
while nums[ind] in res:
ind += 1
if not dp[tar1] and dp[tar1-nums[ind]]: # 如果目标值拼出来了就不用再拼了
dp[tar1-nums[ind]] = False
dp[tar1] = True
elif not dp[tar2] and dp[tar2-nums[ind]]:
dp[tar2-nums[ind]] = False
dp[tar2] = True
else:
dp[nums[ind]] = True
ind += 1
if dp[tar1] and dp[tar2]:
return True
else:
return False
nums = [i for i in range(1,10)]
length = len(nums)
res = []
result = [0]
dfs(0,0,0)
print(result[0] * 8) # 每种形状有八种变换